备战2022年广东高考数学仿真卷（14）

这是一份备战2022年广东高考数学仿真卷（14），文件包含备战2022年广东高考数学仿真卷14解析版docx、备战2022年广东高考数学仿真卷14原卷版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。
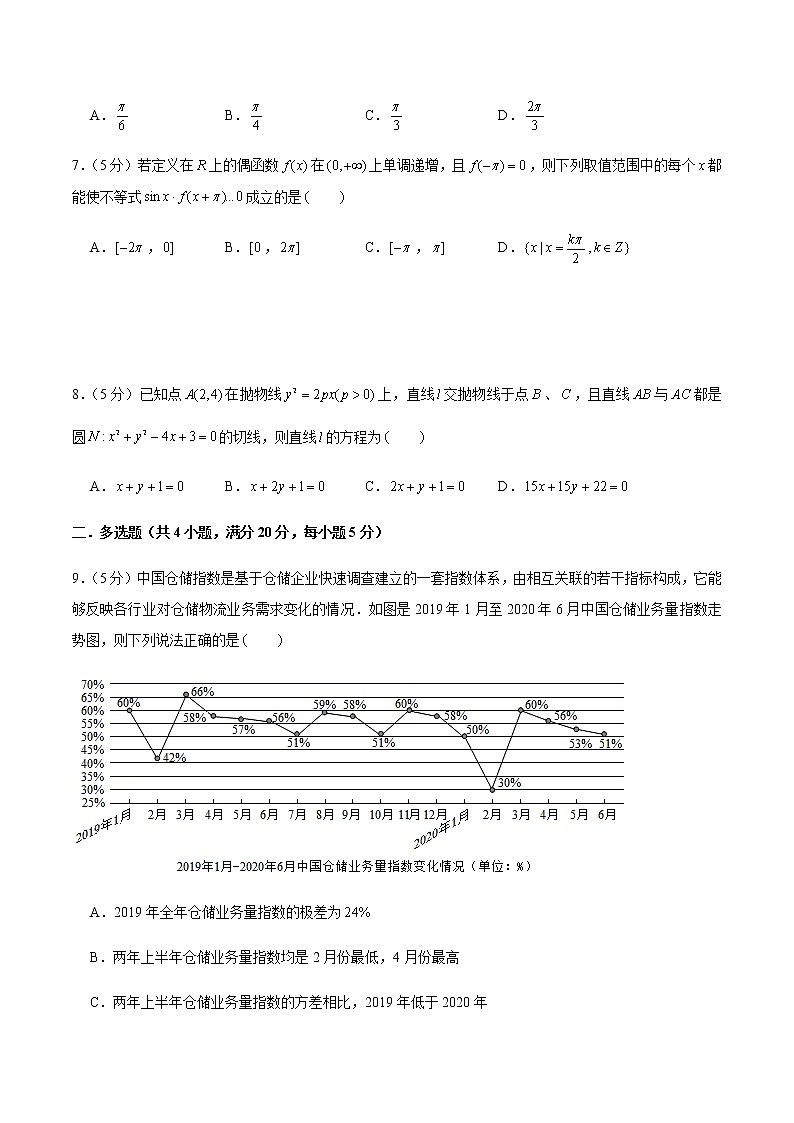
备战2022年广东高考数学仿真卷（14）一．选择题（共8小题，满分40分，每小题5分）1．（5分）已知集合，，0，1，2，，，则　　A．，1，2， B．，2， C．，1， D．，1，2，2．（5分）复数的虚部为　　A． B． C． D．3．（5分）双曲线的虚轴长是实轴长的2倍，则实数的值是　　A．16 B． C． D．4．（5分）设，，，则　　A． B． C． D．5．（5分）如图，圆柱的轴截面是正方形，，分别是和的中点，是弧的中点，则经过、、的平面与圆柱侧面相交所得到的曲线的离心率是　　A．1 B． C． D．6．（5分）已知是单位向量，且，若向量，则与的夹角为　　A． B． C． D．7．（5分）若定义在上的偶函数在上单调递增，且，则下列取值范围中的每个都能使不等式成立的是　　A．， B．， C．， D．  8．（5分）已知点在抛物线上，直线交抛物线于点、，且直线与都是圆的切线，则直线的方程为　　A． B． C． D．二．多选题（共4小题，满分20分，每小题5分）9．（5分）中国仓储指数是基于仓储企业快速调查建立的一套指数体系，由相互关联的若干指标构成，它能够反映各行业对仓储物流业务需求变化的情况．如图是2019年1月至2020年6月中国仓储业务量指数走势图，则下列说法正确的是　　A．2019年全年仓储业务量指数的极差为 B．两年上半年仓储业务量指数均是2月份最低，4月份最高 C．两年上半年仓储业务量指数的方差相比，2019年低于2020年 D．2019年仓储业务量指数的中位数为10．（5分）正方体中，下列结论正确的是　　A．直线与直线所成角为 B．直线与平面所成角为 C．二面角的大小为 D．平面平面11．（5分）设数列的前项和，，为常数），则下列命题中正确的是　　A．若，则不是等差数列 B．若，，，则是等差数列 C．若，，，则是等比数列 D．若，，，则是等比数列12．（5分）已知曲线的方程为，集合，，，若对于任意的，，都存在，，使得成立，则称曲线为曲线，下列方程所表示的曲线中，曲线的序号是　　A． B． C． D．．三．填空题（共4小题，满分20分，每小题5分）13．（5分）函数且的图象恒过定点，若点在直线上，其中，，则的最大值为　　．14．（5分）某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课各1节，则在课程表上的相邻两节文化课之间最多间隔1节艺术课的概率为　　（用数字作答）．15．（5分）函数的最大值为　　，记函数取到最大值时的，则　　．16．（5分）在中，角，，的对边分别为，，，，，若有最大值，则实数的取值范围是 　　．四．解答题（共6小题，满分70分）17．（10分）在条件：①，，②，，③，中任选一个，补充到下面问题中，并给出解答．在中，角，，的对边分别为，，，且，______，求的面积．      18．（12分）已知数列的前项和为，且，．数列是公差大于0的等差数列，，且，，成等比数列．（1）求数列和的通项公式；（2）若，求．           19．（12分）如图，在四棱锥中，四边形是直角梯形，，，底面，，，是的中点．（Ⅰ）求证：平面平面；（Ⅱ）若二面角的余弦值为，求的值；（Ⅲ）在（Ⅱ）的条件下求直线与平面所成角的正弦值．      20．（12分）某商城玩具柜台元旦期间促销，购买甲、乙系列的盲盒，并且集齐所有的产品就可以赠送元旦礼品．而每个甲系列盲盒可以开出玩偶，，中的一个，每个乙系列盲盒可以开出玩偶，中的一个．（1）记事件：一次性购买个甲系列盲盒后集齐，，玩偶；事件：一次性购买个乙系列盲盒后集齐，玩偶；求概率及；（2）礼品店限量出售甲、乙两个系列的盲盒，每个消费者每天只有一次购买机会，且购买时，只能选择其中一个系列的一个盲盒．通过统计发现：第一次购买盲盒的消费者购买甲系列的概率为，购买乙系列的概率为；而前一次购买甲系列的消费者下一次购买甲系列的概率为，购买乙系列的概率为；前一次购买乙系列的消费者下一次购买甲系列的概率为，购买乙系列的概率为；如此往复，记某人第次购买甲系列的概率为．①；②若礼品店每卖出一个甲系列的盲盒可获利20元，卖出一个乙系列的盲盒可获利15元，由样本估计总体，若礼品店每天可卖出1000个盲盒，且买的人之前都已购买过很多次这两个系列的盲盒，试估计该礼品店每天利润为多少元？．              21．（12分）已知圆与定直线，且动圆与圆外切并与直线相切．（1）求动圆圆心的轨迹的方程；（2）已知点是直线上一个动点，过点作轨迹的两条切线，切点分别为，①求证：直线过定点．②求证：．             22．（12分）设函数，．（1）当时，证明：；（2）当时，证明：有唯一零点．