安徽师范大学附属中学2022届高三下学期适应性考试理科数学试题

这是一份安徽师范大学附属中学2022届高三下学期适应性考试理科数学试题，共22页。试卷主要包含了已知集合，，则，非零向量满足，则与的夹角为，已知函数，则函数的图象可能是等内容，欢迎下载使用。
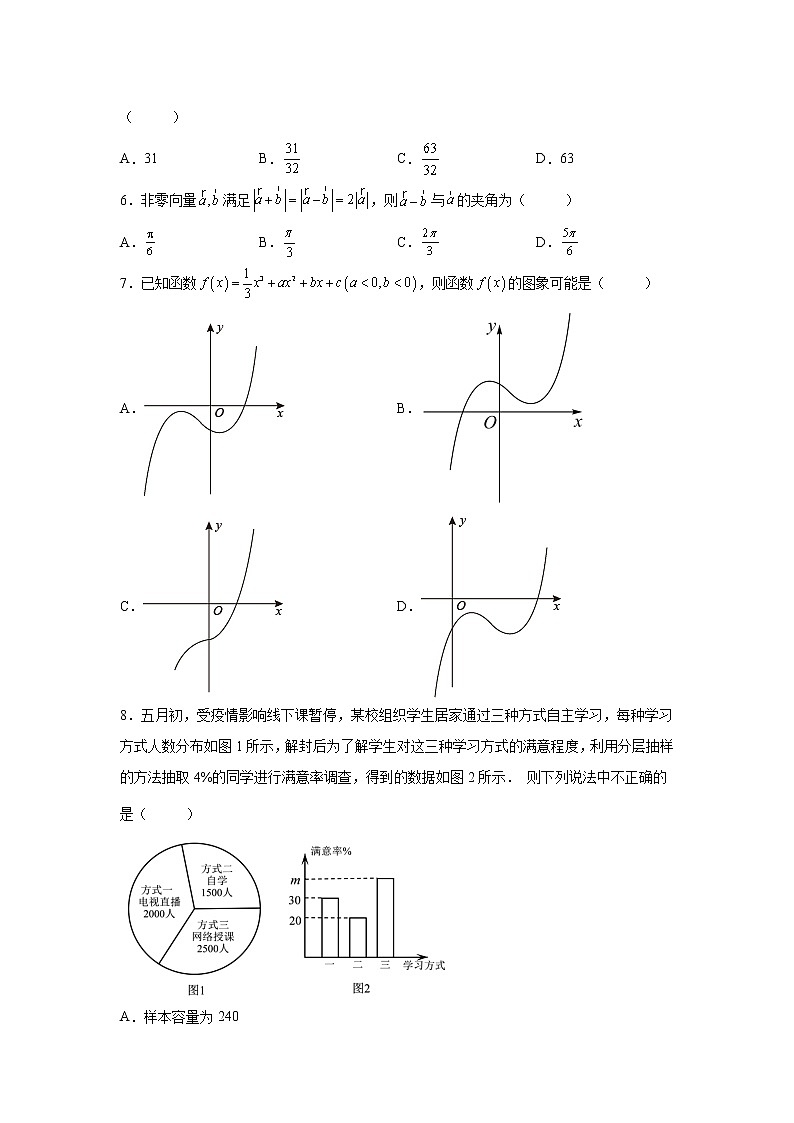
安徽师范大学附属中学2022届高三下学期适应性考试理科数学试题第I卷（选择题）评卷人得分  一、单选题1．已知集合，，则（       ）A． B． C． D．2．若复数，在复平面内对应的点关于轴对称，且，则复数 （     ）A．  B． C． D．3．已知函数的定义域为R，则“是奇函数”是“是奇函数”的（       ）A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件4．已知，，，则执行如图所示的框图输出的结果为（       ）A．a B．b C．c D．无法确定5．已知正项等比数列首项为1，且成等差数列，则前6项和为（       ）A．31 B． C． D．636．非零向量满足，则与的夹角为（       ）A． B． C． D．7．已知函数，则函数的图象可能是（       ）A． B．C． D．8．五月初，受疫情影响线下课暂停，某校组织学生居家通过三种方式自主学习，每种学习方式人数分布如图1所示，解封后为了解学生对这三种学习方式的满意程度，利用分层抽样的方法抽取4%的同学进行满意率调查，得到的数据如图2所示． 则下列说法中不正确的是（       ）A．样本容量为240B．若，则本次自主学习学生的满意度不低于四成C．总体中对方式二满意的学生约为300人D．样本中对方式一满意的学生为24人9．已知，点满足方程，且有，则的取值范围是（       ）A． B． C． D．10．已知函数的对称轴方程为，且，则的单调递增区间是（       ）A． B．C． D．11．如图，在三棱柱中，过的截面与AC交于点D，与BC交于点E，该截面将三棱柱分成体积相等的两部分，则（       ）A． B． C． D．12．已知函数f，若函数的图象上存在两个点，，满足，则a的取值范围为（       ）A． B． C． D．第II卷（非选择题）评卷人得分  二、解答题13．已知实数满足，则的最大值为___________．14．如图，圆内接四边形ABCD中，，，．(1)求边的长；(2)设，，求的值．15．如图，菱形中，把沿折起，使得点至处． (1)证明：平面平面；(2)若与平面所成角的余弦值为，求二面角的余弦值．16．已知椭圆的离心率为，且过点．(1)求椭圆的标准方程与焦距；(2)若直线与椭圆交于两点，记线段AB的中点为，证明：．17．中国象棋历史悠久，属于二人智力对抗性游戏，由于用具简单趣味性强，成为流行极为广泛的棋艺活动．马在象棋中是“威风八面”的棋子，有诗为赞：“马起盘格势，折冲千里余．江河不可障，飒沓入敌虚”．若将矩形棋盘视作坐标系，棋盘的左下角为坐标原点，则马每一步从可移动到或．(1)如上左图，若马从处出发，等可能地向各个能到达（不离开棋盘）的方向移动，求其2步以内到达棋盘上位置的概率；(2)如上右图，在一个更大的棋盘上，马从处出发，每一步仅向轴的正方向移动，最终到达棋盘右上角，若选择每一条可行的道路是等可能的，求马停留在线段上次数的数学期望．18．已知函数的图象在原点处与轴相切．(1)求的值；(2)数列满足：，求证：数列单调递减．参考数据：．19．如图，在直角坐标系中，以原点为极点，x轴正半轴为极轴建立极坐标系. 图中的心型曲线的极坐标方程为，曲线的参数方程为 （t为参数）(1)求曲线的极坐标方程；(2)若曲线与交于三点，求的值.20．已知函数.(1)解关于x的不等式；(2)若不等式恒成立，求实数a的取值范围.评卷人得分  三、填空题21．的展开式中，常数项是______．22．已知抛物线的焦点为F，准线为l，过F的直线m与E交于A，B两点，的垂直平分线分别交l和x轴于P，Q两点.若，则__________.23．正项数列满足，记表示不超过的最大整数，则_______．
参考答案：1．B【解析】【分析】首先根据指数函数的性质求出集合，再根据并集的定义计算可得；【详解】解：因为，，所以；故选：B2．C【解析】【分析】根据复数的几何意义及对称性，得出复数，再利用复数的除法法则即可求解.【详解】由题意知，复数在复平面内对应的点，因为复数，在复平面内对应的点关于轴对称，所以复数在复平面对应的点为，即，则，故选：C．3．A【解析】【分析】根据充分条件、必要条件的定义判断即可；【详解】解：若为奇函数，则，则为奇函数，故充分性成立；若是奇函数，令，则 ，此时无法得到，故必要性不成立，故“是奇函数”是“是奇函数”的充分不必要条件；故选：A4．B【解析】【分析】按照程序框图的流程图进行计算，得到结果.【详解】令，，令，，输出.故选：B5．C【解析】【分析】利用等差数列的通项公式及等比数列的前项和公式即可求解.【详解】∵成等差数列，∴，∴，即，解得 或 ，又∵，∴，∴，故选：C.6．B【解析】【分析】根据给定条件，求出，再利用向量夹角公式计算作答.【详解】由得：，即，解得，因此，，而，解得，所以与的夹角为.故选：B7．B【解析】【分析】根据导函数的零点与原函数极值点的关系即可判定图像.【详解】由题，导函数有两个变号零点即原函数有两个极值点，且，只有B图符合.故选：B.8．B【解析】【分析】对A，根据总人数抽取4%的同学进行计算判断即可；对B，根据统计图计算样本总体满意度进行判断即可；对C，根据方式二中总人数和样本满意度计算判断即可；对D，根据满意率计算即可【详解】对A，由饼图可得总人数为，故样本容量为，故A正确；对B，当时，满意的人数为，故满意度为，故B错误；对C，总体中对方式二满意的学生约为人，故C正确；对D，样本中对方式一满意的学生为人，故D正确；故选：B9．B【解析】【分析】根据双曲线的定义，得到点的轨迹表示以为焦点的双曲线的右支，进而求得双曲线的渐近线方程，结合双曲线的几何性质，即可求解.【详解】由题意，点且满足，根据双曲线的定义，可得点的轨迹表示以为焦点的双曲线的右支，其中，可得，则，可得双曲线的渐近线方程为，又因为点满足方程，即，结合双曲线的几何性质，可得，即的取值范围是.故选：B.10．B【解析】【分析】由题知最小正周期为，即，进而得，故或，再结合得，再整体代换求解单调区间即可.【详解】解：因为函数的对称轴方程为，故令得，得，所以，是函数相邻的两条对称轴，所以，其最小正周期为，即，所以，由于是函数的一条对称轴，所以，所以或，所以或，因为，所以，所以，所以，解得，所以的单调递增区间是.故选：B11．D【解析】【分析】利用棱柱，棱台的体积公式结合条件即得.【详解】由题可知平面与棱柱上，下底面分别交于，，则∥，，显然是三棱台，设的面积为1，的面积为S，三棱柱的高为h，，解得，由，可得.故选：D.12．C【解析】【分析】确定函数的奇偶性与单调性，分析得出只能在轴同一侧，然后不妨设两点都在轴右侧，不等式变形为，设，设，，不等式即为，因此利用导数求得的图象过原点的切线斜率后可得结论．【详解】由函数解析式，时，，，时，，，综上，为偶函数，易知时，单调递增，时，单调递减，显然有，因此要使得成立，则，即两点在的同侧，由是偶函数，不妨设两点都在轴右侧，即在的图象上，，，，等价于存在使得，设，，设的图象过原点的切线的切点为，所以，解得，，所以（）的图象过原点的切线斜率为1，即（）的图象上的点与原点连线的斜率的最小值是1，设，，则为(*)，要使得存在使得(*)式成立，则，又，所以．故选：C．【点睛】关键点点睛：本题难点在于将不等式变形为，设，，不等式转化为能成立，需要学生有较强的等价转化能力.13．0【解析】【分析】作出不等式组表示的平面区域，再利用目标函数的几何意义计算作答.【详解】作出不等式组表示的平面区域，如图中阴影（含边界），其中，目标函数，即表示斜率为2，纵截距为z的平行直线系，画出直线，显然直线经过点A，其纵截距是经过阴影且斜率为2，纵截距为z的平行直线系中最大的，所以的最大值为0.故答案为：014．(1)；(2).【解析】【分析】（1）利用圆内接四边形的性质，结合余弦定理计算作答.（2）在△ABC中，利用正弦定理求出，再利用诱导公式、差角的正弦公式计算作答.(1)圆内接四边形ABCD中，，在△ACD中，由余弦定理得，所以边的长是.(2)依题意，，在△ABC中，，为钝角，由正弦定理得：，即，而为锐角，则，所以.15．(1)证明见解析(2)【解析】【分析】（1）设，连接PO，证得，根据，证得，利用线面垂直的判定定理证得BD⊥平面PAC，进而证得平面PAC⊥平面ABCD.（2）在平面内，作，建立空间直角坐标系，由为与平面所成角，求得，分别求得平面和平面的法向量，结合向量的夹角公式，即可求解.(1)证明：设，连接PO，在菱形ABCD中，O为BD中点，且，因为，所以，又因为，且PO，AC平面PAC，所以BD⊥平面PAC，因为BD平面ABCD，所以平面PAC⊥平面ABCD.(2)解：在平面内，作，以{，，}为x，y，z轴，建立空间直角坐标系，如图所示，设，则，由（1）知平面平面，所以为与平面所成角，所以，可得，又由，所以，设平面的法向量为，则，取，可得，所以，设平面的法向量为，则，取，可得，所以，搜易，由图可知二面角为锐角，故其余弦值为.16．(1)椭圆的标准方程为，焦距为；(2)证明见解析.【解析】【分析】（1）由已知可得，再由离心率求出a及半焦距c作答.（2）联立直线l与椭圆C的方程，利用韦达定理结合平面向量数量积计算得，再利用直角三角形性质推理作答.(1)因为椭圆经过点，且离心率为，则，，解得，半焦距，所以椭圆C的标准方程为，焦距为.(2)由得，设，则有，而，因此，于是得，即，而M为直角三角形ABN斜边AB的中点，则，所以.17．(1)(2)【解析】【分析】（1）先求出从出发2步以内到达P（3，3）且不出棋盘的走法共有2种，再根据分布乘法原理，即可求解；（2）先求出马共走的步数，然后写出随机变量的所有可能取值，求出对应概率，从而可求得分布列，再根据期望公式求出期望即可.(1)解：从出发2步以内到达P（3，3）且不出棋盘的走法共有2种，记第i种路线的概率为，则：，因此总概率为；(2)解：设马有m步从（x，y）走到，n步走到），则，解得，即马共走了6步，总路径数为，路径上经过的点可能在线段上的有（3，3），（6，6），（9，9）共3个，因此可取1，2，3，因此，所以马停留在线段上次数X的分布列为：Xl23P 所以X的数学期望.18．(1)(2)证明见解析【解析】【分析】（1）求导，根据题意结合导数的几何意义可得，从而可得出答案；（2）构造函数，求出函数的导函数，利用导数求出函数的最小值，证明，即可得证.(1)解：∵，∴，∵函数的图象在原点处与轴相切，∴，∴；(2)解：因为，所以，令，则，设，则，所以函数在上递增，而，所以存在，当时，递减，当时，递增，而，所以，即当时，，而，所以{}是递减数列.【点睛】本题考查了导数的几何意义，考查了利用导数求函数的单调区间及最值，考查了转化思想，在求函数的最值时关键在于二次求导.19．(1)和或；(2)2.【解析】【分析】（1）先化为直角坐标，在化为极坐标方程即可求出答案.（2）写出极坐标系下点与的坐标，再利用即可取出答案.(1)曲线的直角坐标方程为，则极坐标方程为：和或(2)设，则.20．(1)(2)【解析】【分析】（1）讨论不同取值范围对原绝对值不等式化简求解再取并集即可；（2）当时不等式恒成立，则；当时，先进行参变分离，再利用绝对值三角不等式求解即可.(1)因为，所以或或，解得或或，所以，即原不等式的解集为.(2)当时，不等式恒成立，此时；当时，不等式可转化为，因为，当且仅当，即时等号成立，所以.所以实数a的取值范围为.21．【解析】【分析】将三项式转化为，根据展开式的通项，可知当时取得常数项.【详解】，展开式的通项为，当，即时，可得展开式的常数项为.故答案为：.22．【解析】【分析】根据题意可得，由于对角线与垂直，得四边形是菱形，在由抛物线的定义即可得到为等边三角形，可得直线的方程，把直线和抛物线进行联立，进而求得答案.【详解】垂直平分，，在四边形中，对角线与垂直，四边形是菱形，由抛物线的定义可得：故     为等边三角形故 故 故直线 故把直线与抛物线进行联立得，设 ，则故答案为：.23．18【解析】【分析】先求得，再利用放缩，再根据裂项相消求和求解即可【详解】因为，故，因为正项数列，故.又，当时，，故.又对于都有，故，故，故故答案为：18