




2022年中考数学三轮冲刺过关回归教材重难点10 二次函数的实际应用-【查漏补缺】
展开回归教材重难点10 二次函数的实际应用
二次函数的实际应用是初中《二次函数》章节的重点内容,考查的相对比较综合,把二次函数图像与性质结合起来,联系实际应用综合考查。在中考数学中,主要是以解答题形式出现。通过熟练二次函数性质,提升数学学科素养,提高逻辑思维推断能力。
本考点是中考五星高频考点,在全国各地的中考试卷中均有出现,题目难度中等,甚至有些地方将其作为解答题的压轴题。
二次函数图象上点的坐标特征:解题时,需熟悉抛物线的有关性质:抛物线的开口向上,则抛物线上的点离对称轴越远,对应的函数值就越大.
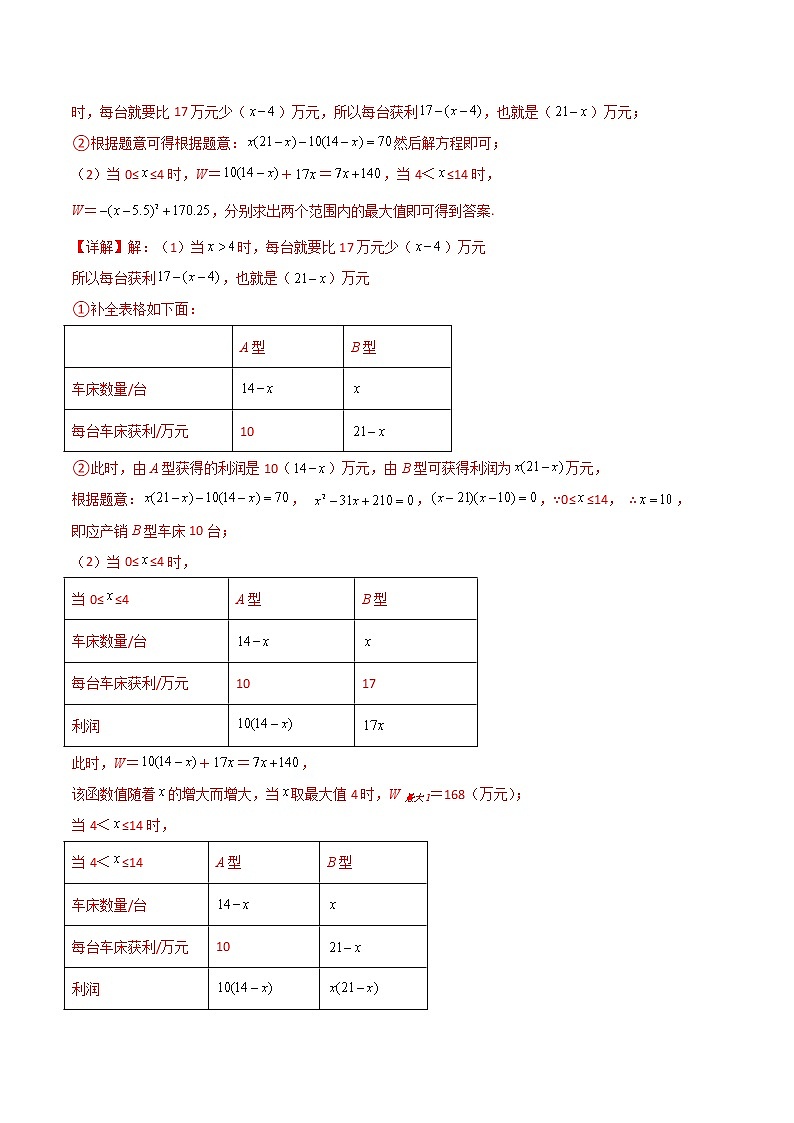
1.(辽宁省盘锦市2021年中考数学真题试卷)某工厂生产并销售A,B两种型号车床共14台,生产并销售1台A型车床可以获利10万元;如果生产并销售不超过4台B型车床,则每台B型车床可以获利17万元,如果超出4台B型车床,则每超出1台,每台B型车床获利将均减少1万元.设生产并销售B型车床台.
(1)当时,完成以下两个问题:
①请补全下面的表格:
| A型 | B型 |
车床数量/台 | ________ | |
每台车床获利/万元 | 10 | ________ |
②若生产并销售B型车床比生产并销售A型车床获得的利润多70万元,问:生产并销售B型车床多少台?
(2)当0<≤14时,设生产并销售A,B两种型号车床获得的总利润为W万元,如何分配生产并销售A,B两种车床的数量,使获得的总利润W最大?并求出最大利润.
2.(江苏省淮安市2021年中考数学真题)某超市经销一种商品,每件成本为50元.经市场调研,当该商品每件的销售价为60元时,每个月可销售300件,若每件的销售价每增加1元,则每个月的销售量将减少10件.设该商品每件的销售价为x元,每个月的销售量为y件.
(1)求y与x的函数表达式;
(2)当该商品每件的销售价为多少元时,每个月的销售利润最大?最大利润是多少?
3.(贵州省遵义市2021年中考数学真题试卷)为增加农民收入,助力乡村振兴.某驻村干部指导农户进行草莓种植和销售,已知草莓的种植成本为8元/千克,经市场调查发现,今年五一期间草莓的销售量y(千克)与销售单价x(元/千克)(8≤x≤40)满足的函数图象如图所示.
(1)根据图象信息,求y与x的函数关系式;
(2)求五一期间销售草莓获得的最大利润.
4.(湖北省荆门市2021年中考数学真题)某公司电商平台,在2021年五一长假期间,举行了商品打折促销活动,经市场调查发现,某种商品的周销售量y(件)是关于售价x(元/件)的一次函数,下表仅列出了该商品的售价x,周销售量y,周销售利润W(元)的三组对应值数据.
x | 40 | 70 | 90 |
y | 180 | 90 | 30 |
W | 3600 | 4500 | 2100 |
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)若该商品进价a(元/件),售价x为多少时,周销售利润W最大?并求出此时的最大利润;
(3)因疫情期间,该商品进价提高了m(元/件)(),公司为回馈消费者,规定该商品售价x不得超过55(元/件),且该商品在今后的销售中,周销售量与售价仍满足(1)中的函数关系,若周销售最大利润是4050元,求m的值.
5.(内蒙古鄂尔多斯2021年中考数学试题)鄂尔多斯市某宾馆共有50个房间供游客居住,每间房价不低于200元且不超过320元、如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.已知每个房间定价x(元)和游客居住房间数y(间)符合一次函数关系,如图是y关于x的函数图象.
(1)求y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当房价定为多少元时,宾馆利润最大?最大利润是多少元?
6.(2021年河南省南阳市卧龙区中考数学二模试卷)某地积极响应国家乡村振兴的号召,决定成立草莓产销合作社,负责对农户种植草莓的技术指导和统一销售,所获利润年底分红.经市场调研发现,草莓销售单价y(万元)与产量x(吨)之间的关系如图所示(0<x≤100).已知草莓的产销投入总成本p(万元)与产量x(吨)之间满足p=x+1.
(1)直接写出草莓销售单价y(万元)与产量x(吨)之间的函数关系式.
(2)为提高农户种植草莓的积极性,合作社决定按每吨0.3万元的标准奖励种植户,为确保合作社所获利润w(万元)不低于55万元,产量至少要达到多少吨?
7.(2021年山东省菏泽市东明县中考数学四模试题)某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售单价25元/件时,每天的销售量是250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每件文具的利润不低于25元且不高于29元.
请比较哪种方案的最大利润更高,并说明理由.
8.(2022年浙江省温州外国语学校中考数学一模试题)随着电商时代发展, 某水果商以 “线上”与 “线下”相结合的方式销售我市瓯柑共1000箱, 已知“线上”销售的每箱利润为50元. “线下”销售的每箱利润 (元) 与销售量箱之间的函数关系如图中的线段 .
(1)求与之间的函数关系.
(2)当“线下”的销售利润为28000元时,求的值.
(3)实际“线下”销售时,每箱还要支出其它费用, 若“线上”与“线下”售完这1000箱瓯柑所获得的最大总利润为56250元, 请求出的值.
9.(2021年河北省九地市中考数学模拟试卷(二))某文具店计划在40天内销售一种成本为15元本的笔记本,该种笔记本的日销售量p(本)和销售天数x(单位:天,1≤x≤40,且x为正整数)之间满足一次函数关系,且其图象经过点(10,40),(40.10),当1≤x≤20时,销售单价q(元)和销售天数x(天)之间的部分对应值如表所示.
销售天数x/天 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
销售单价q/元 | 30.5 | 31 | 31.5 | 32 | 32.5 | 33 | 33.5 | 34 | ... |
当21≤x≤40时,销售单价q(元)和销售天数x(天)之间满足
(1)求销售到第几天时,该种笔记本的销售单价为45元
(2)求出日销售量P与销售天数x的函数解析式
(3)设该文具店第x天获得的利润为y元,请求出y关于x的函数解析式
(4)在这40天中,该文具店第几天能够获利870元?
10.(2021年江苏省南通市中考数学第二次适应性训练试卷)某宾馆共有80个房间可供顾客居住.宾馆负责人根据前几年的经验作出预测:今年5月份,该宾馆每天的房间空闲数y(间)与每天的定价x(元/间)之间满足某个一次函数关系,且部分数据如表所示.
每天的定价x(元/间) | 208 | 228 | 268 | … |
每天的房间空闲数y(间) | 10 | 15 | 25 | … |
(1)该宾馆将每天的定价x(元/间)确定为多少时,所有的房间恰好被全部订完?
(2)如果宾馆每天的日常运营成本为5000元,另外,对有顾客居住的房间,宾馆每天每间还需支出28元的各种费用,那么单纯从利润角度考虑,宾馆应将房间定价确定为多少时,才能获得最大利润?并请求出每天的最大利润.
11.(2021年山东省青岛市局属四校中考数学一模试卷)某商场销售一种小商品,进货价为8元/件.当售价为10元/件时,每天的销售量为100件.在销售过程中发现:销售单价每上涨0.1元,每天的销售量就减少1件.设销售单价为x(元/件)(x≥10),每天销售利润为y(元).
(1)直接写出y与x的函数关系式为: ;
(2)若要使每天销售利润为270元,求此时的销售单价;
(3)若每件该小商品的利润率不超过100%,且每天的进货总成本不超过800元,求该小商品每天销售利润y的取值范围.
中考数学三轮冲刺过关 回归教材重难点10 二次函数的实际应用: 这是一份中考数学三轮冲刺过关 回归教材重难点10 二次函数的实际应用,文件包含中考数学三轮冲刺过关回归教材重难点10二次函数的实际应用教师版docx、中考数学三轮冲刺过关回归教材重难点10二次函数的实际应用学生版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
2022年中考数学三轮冲刺过关回归教材重难点11 二次函数与几何的综合应用-【查漏补缺】: 这是一份2022年中考数学三轮冲刺过关回归教材重难点11 二次函数与几何的综合应用-【查漏补缺】,文件包含回归教材重难点11二次函数与几何的综合应用解析版docx、回归教材重难点11二次函数与几何的综合应用原卷版docx等2份试卷配套教学资源,其中试卷共50页, 欢迎下载使用。
2022年中考数学三轮冲刺过关回归教材重难点09 圆的综合问题-【查漏补缺】: 这是一份2022年中考数学三轮冲刺过关回归教材重难点09 圆的综合问题-【查漏补缺】,文件包含回归教材重难点09圆的综合问题解析版docx、回归教材重难点09圆的综合问题原卷版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。












