2022年中考数学三轮冲刺过关回归教材重难点12 三角形与四边形的综合应用-【查漏补缺】

回归教材重难点12 三角形与四边形综合应用

三角形与四边形综合应用是初中《特殊平行四边形》章节的重点内容，考查的相对比较综合，把图像图形的性质结合起来，联系图形的几何变换考查。在中考数学中，主要是以解答题形式出现。通过熟练掌握图形的性质与几何变换，提升数学学科素养，提高逻辑思维推断能力。

本考点是中考五星高频考点，在全国各地的中考试卷中均有出现，题目难度较大，甚至有些地方将其作为解答题的压轴题。

1．全等三角形的判定与性质

（1）全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．

（2）在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．

2．直角三角形斜边上的中线

（1）性质：在直角三角形中，斜边上的中线等于斜边的一半．（即直角三角形的外心位于斜边的中点）

（2）定理：一个三角形，如果一边上的中线等于这条边的一半，那么这个三角形是以这条边为斜边的直角三角形．

3．相似三角形的判定与性质

三角形相似的判定一直是中考考查的热点之一，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形；或依据基本图形对图形进行分解、组合；或作辅助线构造相似三角形，判定三角形相似的方法有事可单独使用，有时需要综合运用，无论是单独使用还是综合运用，都要具备应有的条件方可．

4．三角形、四边形、几何变换运用

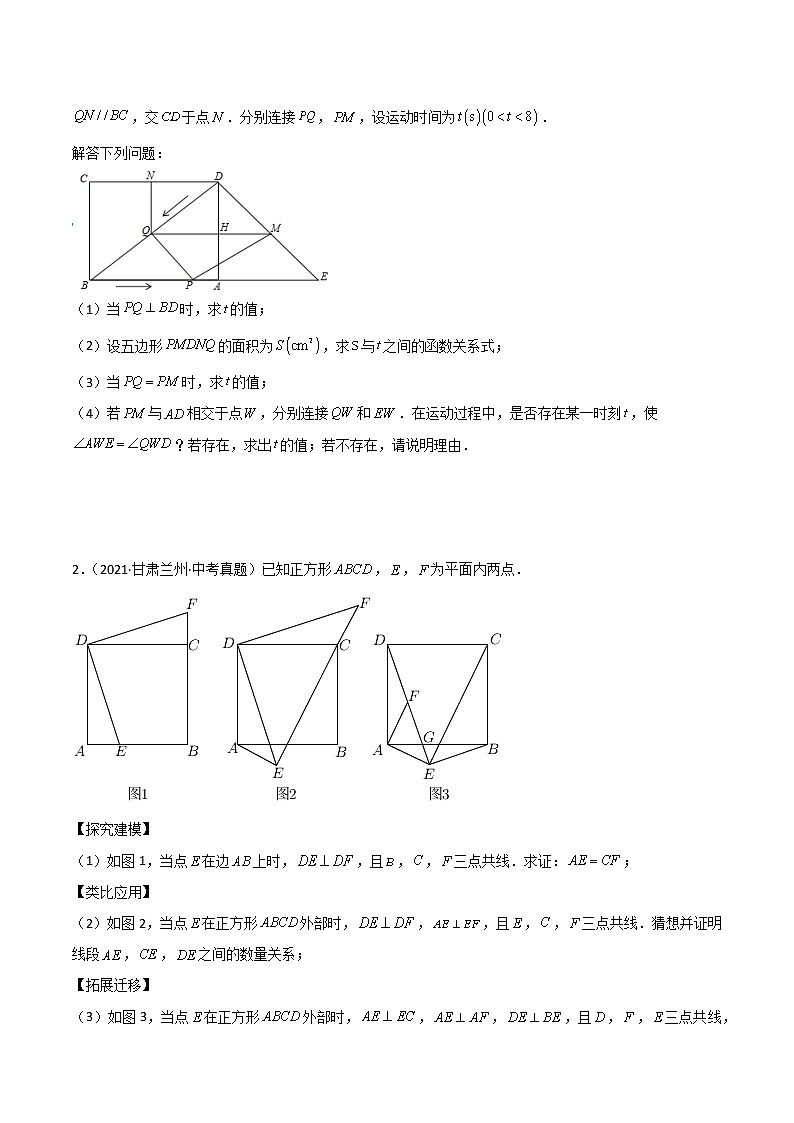
1．（2021·山东青岛·中考真题）已知：如图，在矩形和等腰中，，，．点从点出发，沿方向匀速运动．速度为；同时，点从点出发，沿方向匀速运动，速度为．过点作，交于点，交于点，过点作

，交于点．分别连接，，设运动时间为．

解答下列问题：

（1）当时，求的值；

（2）设五边形的面积为，求与之间的函数关系式；

（3）当时，求的值；

（4）若与相交于点，分别连接和．在运动过程中，是否存在某一时刻，使？若存在，求出的值；若不存在，请说明理由．

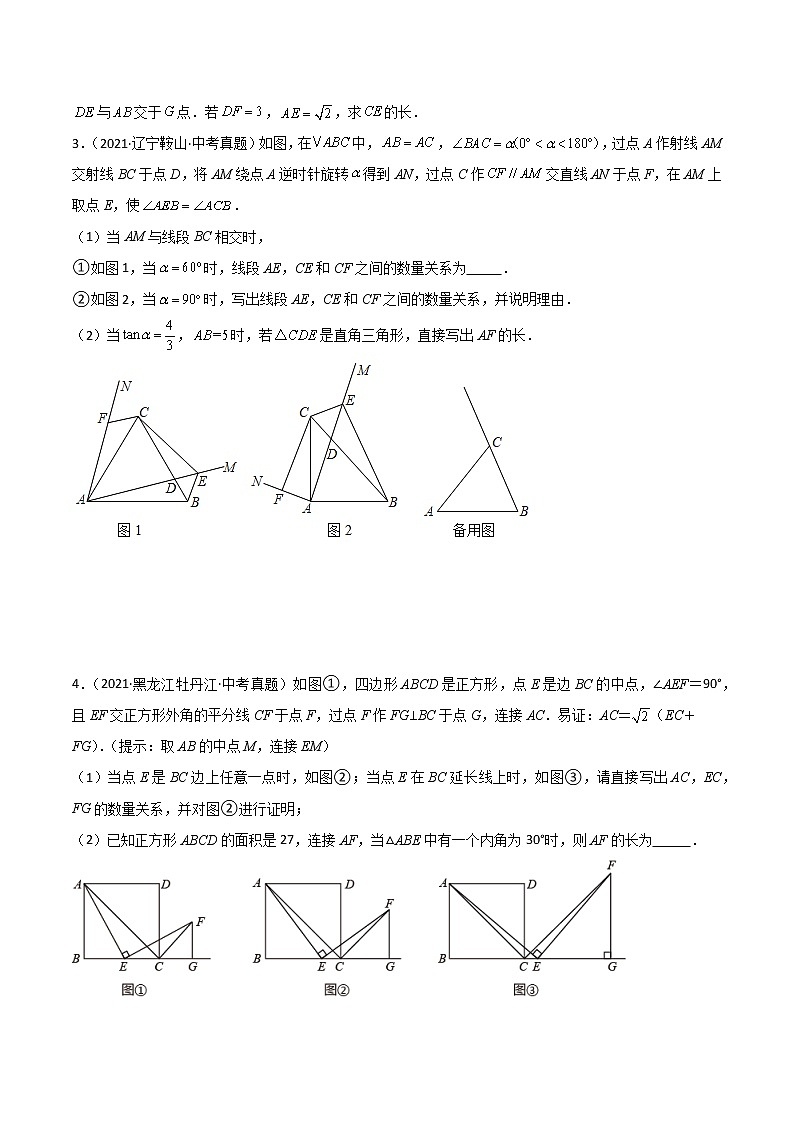
2．（2021·甘肃兰州·中考真题）已知正方形，，为平面内两点．

【探究建模】

（1）如图1，当点在边上时，，且，，三点共线．求证：；

【类比应用】

（2）如图2，当点在正方形外部时，，，且，，三点共线．猜想并证明线段，，之间的数量关系；

【拓展迁移】

（3）如图3，当点在正方形外部时，，，，且，，三点共线，

与交于点．若，，求的长．

3．（2021·辽宁鞍山·中考真题）如图，在中，，，过点A作射线AM交射线BC于点D，将AM绕点A逆时针旋转得到AN，过点C作交直线AN于点F，在AM上取点E，使．

（1）当AM与线段BC相交时，

①如图1，当时，线段AE，CE和CF之间的数量关系为 　　．

②如图2，当时，写出线段AE，CE和CF之间的数量关系，并说明理由．

（2）当，时，若是直角三角形，直接写出AF的长．

4．（2021·黑龙江牡丹江·中考真题）如图①，四边形ABCD是正方形，点E是边BC的中点，∠AEF＝90°，且EF交正方形外角的平分线CF于点F，过点F作FG⊥BC于点G，连接AC．易证：AC（EC＋FG）．（提示：取AB的中点M，连接EM）

（1）当点E是BC边上任意一点时，如图②；当点E在BC延长线上时，如图③，请直接写出AC，EC，FG的数量关系，并对图②进行证明；

（2）已知正方形ABCD的面积是27，连接AF，当△ABE中有一个内角为30°时，则AF的长为 　 　．

5．（2021·四川成都·中考真题）在中，，将绕点B顺时针旋转得到，其中点A，C的对应点分别为点，．

（1）如图1，当点落在的延长线上时，求的长；

（2）如图2，当点落在的延长线上时，连接，交于点M，求的长；

（3）如图3，连接，直线交于点D，点E为的中点，连接．在旋转过程中，是否存在最小值？若存在，求出的最小值；若不存在，请说明理由．

6．（2021·河南洛阳·一模）如图①，在正方形ABCD中，AB＝5，点F在AC上，且CF＝2，过点F作EF⊥AC于点F，交CD于点E，连接AE，BF．

(1)【问题发现】线段AE与BF的数量关系是     ，直线AE与BF所夹锐角的度数是     ；

(2)【拓展探究】当CEF绕点C顺时针旋转时，上述结论是否成立？若成立，请写出结论，并结合图②给出证明；若不成立，请说明理由；

(3)【解决问题】在（2）的条件下，当点F到直线BC的距离为2时，请直接写出AE的长．

7．（2021·山东临沂·二模）如图1，四边形是正方形，是等边三角形，为对角线（不含点）上的点．

(1)当点是与的交点时，如图1，求的度数；

(2)如图2，若点是上任意一点时，将绕点逆时针旋转得到，连接，，求证：；

(3)当点在何处时，的值最小，说明理由．

8．（2021·江苏常州·一模）中，，，，点D是AB边上的动点，连接CD．

(1)如图1，当是以CD为腰的等腰三角形时，AD长为_______；

(2)如图2，作于点E，作交DE于点F，且，求AE的长；

(3)将沿CD翻折得，若，求的值．

9．（2021·河南·商丘市第一中学一模）如图1所示，在Rt△ABC中，∠C＝90°，∠ABC＝45°，M、N分别是AC、AB的中点，过B作BD⊥MN于D，E是直线MN上一动点，作Rt△BEF使∠BEF＝90°，∠EBF＝45°，连接FN．

(1)【观察猜想】

如图2所示，当E与N重合时，的值为_______；

(2)【问题探究】

如图1所示，当点E与N不重合时，请求出的值及直线FN与MN所夹锐角的度数并说明理由；

(3)【问题解决】

如图3所示，当点A、E、F在同一直线上时，请直接写出的值．

10．（2021·江苏盐城·二模）如图，在矩形ABCD中，AB＝12cm，BC＝9cm，对角线AC、BD相交于点O，点M从点D出发沿DA方向向点A匀速运动，速度为4cm/s，点P同时从D出发，沿DC方向向点C匀速运动，速度为3cm/s．过点M作MN∥BD交AC边于点E，交AB边于点N，连接PO并延长，交AB于Q，连接PM、MQ．设运动时间为t（s）（0＜t＜）．

(1)当t＝时，求MN的长；

(2)设四边形MNQP的面积为S（cm2），求S与t之间的函数关系式；

(3)是否存在某一时刻t，将△MQP沿MQ折叠时，使得点P落在直线AD上？若存在，求出此时t的值，若不存在，说明理由．