回归教材重难点03 立体几何-【查漏补缺】2022年高考数学（文）三轮冲刺过关

这是一份回归教材重难点03 立体几何-【查漏补缺】2022年高考数学（文）三轮冲刺过关，文件包含回归教材重难点03立体几何解析版docx、回归教材重难点03立体几何原卷版docx等2份试卷配套教学资源，其中试卷共43页， 欢迎下载使用。
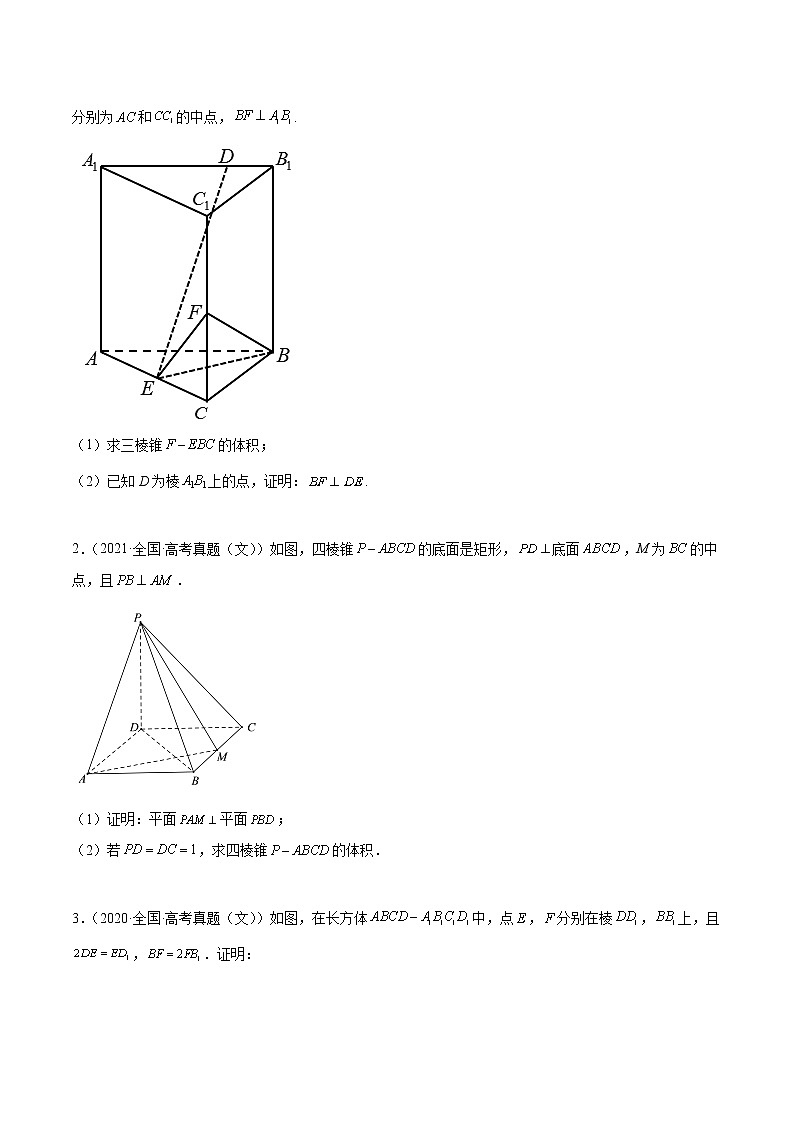
回归教材重难点03 立体几何 立体几何解答题是高考数学必考内容，该考点命题相对稳定，难度中等，是考生必须突破的核心内容之一.高考数学立体几何解答题，主要采用“论证与计算”相结合的方式，在命题上一般包含小问，会涉及到空间点、线、面位置关系的判定与探究，特别是平行与垂直关系的证明；空间角(包括异面直线夹角、直线与平面所成角)或空间距离(包括空间几何体的体积、表面积和点到平面的距离等)的计算.立体几何在解题能力方面的要求是：在数学思想上，一般涉及转化与化归思想、数形结合思想、函数与方程思想；在解题方法上，一般涉及几何法.1.全国卷高考数学立体几何一般设问方式是直接求解空间角、空间距离体积.解决这类问题一般需要先根据题意，通过数学抽象将几何问题转化为代数问题，最后还原到几何体中求解相应的几何量.2.翻折问题主要包含两大问题：平面图形的折叠与几何体的表面展开.这两种方式的转变正是空间几何与平面几何问题转化的集中体现，展开与折叠问题就是一个由抽象到直观，由直观到抽象的过程.解决翻折问题，关键是对翻折前后不变量及不变性的把握，即将翻折前后的图形进行比较，弄清楚哪些角和长度变了，哪些没变(可以观察各面的位置关系变化，同一面上的边角基本不会变)；哪些点、线共面，哪些不共面；翻折后的线与原来的线有什么关系，尤其要注意找出相互平行或垂直的直线.3.解决存在性问题主要有以下方法：几何法，即分析法与综合法并用，一般先假设存在，借助相应的性质定理进行分析推理，得出结论.若存在，再用判定定理证明，即先猜后证；若不存在，则用反证法证明.4.开放性问题相对于存在性问题而言，有其结论的多样性，即结论的不确定性.如果结论是肯定的，需要通过推理论证或者转化为向量运算进行说明；如果是否定的，则需要得出矛盾，利用反证法或者通过数量关系的矛盾性解决.【真题演练】1．（2021·全国·高考真题（文））已知直三棱柱中，侧面为正方形，，E，F分别为和的中点，.（1）求三棱锥的体积；（2）已知D为棱上的点，证明：. 2．（2021·全国·高考真题（文））如图，四棱锥的底面是矩形，底面，M为的中点，且．（1）证明：平面平面；（2）若，求四棱锥的体积． 3．（2020·全国·高考真题（文））如图，在长方体中，点，分别在棱，上，且，．证明：（1）当时，；（2）点在平面内． 4．（2020·全国·高考真题（文））如图，已知三棱柱ABC–A1B1C1的底面是正三角形，侧面BB1C1C是矩形，M，N分别为BC，B1C1的中点，P为AM上一点．过B1C1和P的平面交AB于E，交AC于F．（1）证明：AA1//MN，且平面A1AMN⊥平面EB1C1F；（2）设O为△A1B1C1的中心，若AO=AB=6，AO//平面EB1C1F，且∠MPN=，求四棱锥B–EB1C1F的体积． 5．（2020·全国·高考真题（文））如图，为圆锥的顶点，是圆锥底面的圆心，是底面的内接正三角形，为上一点，∠APC=90°．（1）证明：平面PAB⊥平面PAC；（2）设DO=，圆锥的侧面积为，求三棱锥P−ABC的体积. 【好题演练】1．（2022·陕西榆林·三模（文））如图，在多面体中，底面是正方形，，，底面.(1)证明：平面；(2)若，求该多面体的体积. 2．（2022·山西晋城·二模（文））如图，在几何体中，，，均为边长为的等边三角形，平面平面，平面⊥平面．(1)求证：；(2)求点到平面的距离． 3．（2022·贵州·模拟预测（文））如图，在棱长为2的正方体中，，，，分别是棱，，，的中点. (1)求证：，，，四点共面，记过这四点的平面为，在图中画出平面与该正方体各面的交线（不必说明画法和理由）；(2)求点到（1）中平面的距离. 4．（2022·甘肃·二模（文））风筝起源于春秋时期，是中国古代劳动人民智慧的结晶，北方也称“纸鸢”，虽经变迁，但时至今日放风筝仍是人们喜爱的户外活动.如图，一只风筝的骨架模型是四棱锥，其中于平面.(1)求证：；(2)若，为使风筝保持最大张力，平面与底面所成二面角的正切值应为，求此时到㡳面的距离. 5．（2022·陕西宝鸡·三模（文））如图所示，点在圆柱的上底面圆周上，四边形为圆柱下底面的内接四边形，且为圆柱下底面的直径，为圆柱的母线.且，圆柱的底面半径为1.(1)证明：；(2)若为的中点，点在线段上，，求三棱锥的体积. 6．（2022·江西·上饶市第一中学二模（文））如图，点C是以为直径的圆O上异于A，B的动点，平面，四边形是直角梯形，且. (1)证明：平面；(2)当三棱锥的体积最大时，求点E到平面的距离. 7．（2022·黑龙江·哈尔滨三中二模（文））如图，平面四边形ABCD中，，，，，将三角形ABD沿BD翻折到三角形PBD的位置，平面平面BCD，E为PD中点.(1)求证：；(2)求点B到平面PCD的距离. 8．（2022·贵州·模拟预测（文））如图，在三棱锥中，是边长为4的正三角形，，，O为线段上的一点，点P在底面上的射影为点M.(1)证明：平面.(2)若三棱锥的体积为，求的值. 9．（2022·宁夏石嘴山·一模（文））如图，在四棱锥中，底面为矩形，平面，，，是中点，为上一点.(1)求证：平面；(2)若三棱锥的体积为，求的长. 10．（2022·安徽合肥·二模（文））如图，在矩形中，，点为边的中点，以为折痕把折起，使点到达点的位置，使得，连结，，．(1)证明：平面平面；(2)求点到平面的距离． 11．（2022·河南·汝州市第一高级中学模拟预测（文））如图，在三棱柱中，平面平面，，.(1)求证：；(2)若，，，求点C到平面的距离. 12．（2022·安徽黄山·二模（文））直角梯形中，，，，，，将梯形沿中位线折起使，并连接、得到多面体，连接，，.(1)求证：平面；(2)求到平面的距离. 13．（2022·江西宜春·模拟预测（文））如图，四边形是一个半圆柱的轴截面，E，F分别是弧，上的一点，，点H为线段的中点，且，，点G为线段上一动点.(1)试确定点G的位置，使平面，并给予证明；(2)求三棱锥的体积. 14．（2022·内蒙古呼和浩特·一模（文））如图，四棱锥中，平面ABCD，，，，E、F分别为PB、AB的中点．(1)求证：平面PAD；(2)求点B到平面PCF的距离．