专题53立体几何与空间向量第五缉-备战2022年高中数学联赛之历年真题分类汇编(2015-2021)

这是一份专题53立体几何与空间向量第五缉-备战2022年高中数学联赛之历年真题分类汇编(2015-2021)，文件包含专题53立体几何与空间向量第五缉解析版-备战2022年高中数学联赛之历年真题分类汇编2015-2021docx、专题53立体几何与空间向量第五缉原卷版-备战2022年高中数学联赛之历年真题分类汇编2015-2021docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。
备战2022年高中数学联赛之历年真题分类汇编(2015-2021)
专题53立体几何与空间向量第五缉
1．【2021年吉林预赛】如图,RA⊥ 平面ABCD,RQ//AD ,四边形ABCD为正方形,AD=AR=2RQ=2.E 为BR的中点，M为线段BQ上的动点.
(1)求证：AE⊥CM；
(2)求MC与平面MQD所成角的正弦值的取值范围.

【答案】(1)证明见解析；(2) 49,22.
【解析】(I)因为RQ//AD,AD//BC .
所以RQ//BC .故B、C、Q、R共面.
因为CB⊥ 平面RAB,且AE⊂ 平面RAB.
所以CB⊥AE.
又RB⊥AE ,RRB∩CB=B .
所以AE⊥ 平面BCQR.
又CM⊂ 平面BCQR,
所以AE⊥CM .
(II)如图.以A为坐标原点.建立空间直角坐标系A-xyz ，

则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),R(0,0,2),Q(0,1,2).
平面MQD某为平面DBQ.
DB=(2,-2,0),DQ=(0,-1,2) ，
设平面DBQ的法向量为n→=x,y,z ，
则n⋅DB=0n⋅DQ=0 ，令z=1可得x=2y=2 ，所以n=(2,2,1) .
因为M 为线段BQ上的动点,所以可设CM=λCQ+(1-λ)CB( 共中0⩽λ⩽1).
又CB=(0,-2,0),CQ=(-2,-1,2) ,
所以CM=(-2λ,λ-2,2λ),MC=(2λ,-λ+2,-2λ)
设MC与平面MQD所成角为θ .
则sinθ=|MC⋅n||MC|⋅|n|=43×9λ2-4λ+4=43×9λ-292+329∈49,22 ,
即MC与平面MQD所成角的正弦值的取值范围是49,22 .
2．【2021年全国高中数学联赛A卷一试】如图，正方体的棱长为2，在正方形ABFE的内切圆上任取一点P1,在正方形BCGF的内切圆上任取一点P2,在正方形EFGH的内切圆上任取一点P3.求P1P2+P2P3+P3P1的最小值与最大值.

【答案】最小值为32-3,最大值为36.
【解析】以正方体的中心为原点,DA、DC、DH的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系.
根据条件,可设P11,cosα1,sinα1,P2sinα2,1,cosα2,P3cosα3,sinα3,1.
约定P4=P1,α4=α1.记di=PiPi+1i=1,2,3,
则di2=1-sinαi+12+1-cosαi2+sinαi-cosαi+12 ①
记f=P1P2+P2P3+P3P1.
先求f的最小值.对i=1,2,3,根据①与平均值不等式得di2≥1-sinαi+12+1-cosαi2≥121-sinαi+1+1-cosαi2，
故di≥222-sinαi+1-cosαi.
于是f=d1+d2+d3≥22i=132-sinαi+1-cosαi=32-22i=13sinαi+cosαi
=32-i=13sinαi+π4≥32-3.
当αi=π4i=1,2,3时,f可取到最小值32-3.
再求f的最大值.由①知di2=4-2cosαi-2sinαi+1-2sinαicosαi+1.
注意到sinαi≥-1,cosαi≥-1i=1,2,3,有
i=13di2=12-2i=13sinαi+1+i=13cosαi+i=13sinαicosαi+1=12-2i=13sinαi+i=13cosαi+1+i=13sinαicosαi+1=18-2i=131+sinαi1+cosαi+1≤18.
由柯西不等式知f2≤3d12+d22+d32=54,故f≤36.
当αi=πi=1,2,3时,f可取到最大值36.
综上所述，f的最小值为32-3,最大值为36.
3．【2021年全国高中数学联赛B卷一试】在正nn≥3棱锥P-A1A2⋯An中，O为底面正n边形A1A2⋯An的中心，B为棱A1An的中点.
(1)证明:PO2sin2πn+PA12cos2πn=PB2;
(2)设正n棱锥P-A1A2⋯An的侧棱与底面所成的角为α,侧面与底面所成的角为β,试确定1ni=1ncos∠AiPB与sinα⋅sinβ的大小关系,并予以证明.
【答案】证明见解析
【解析】(1)由于PO⊥底面A1A2⋯An,故∠POA1=∠POB=90∘.
设OA1=r,则OB=OA1⋅cos∠A1OB=rcosπn,
于是有r2+PO2=PA12,r2cos2πn+PO2=PB2.
消去r2得PO21-cos2πn=PB2-PA12cos2πn,
即PO2sin2πn+PA12cos2πn=PB2.
(2)由条件知PO⋅OAi=0i=1,2,⋯,n,PO⋅OB=0.
设正n棱锥的侧棱长为l,
则l⋅PB⋅i=1ncos∠AiPB=i=1nPAi⋅PB⋅cos∠AiPB=i=1nPAi⋅PB=i=1nPO+OAi⋅PO+OB=i=1nPO2+OAi⋅OB=nPO2+OB⋅i=1nOAi=n⋅|PO|2，
最后一步用到了s=i=1nOAi=0(这是因为，O为正n边形A1A2⋯An的中心,各OAii=1,2,⋯,n在逆时针旋转2πn后仍为这些向量的排列,故它们的和向量s逆时针旋转2πn后仍为s,所以s只能为零向量).
于是1ni=1ncos∠AiPB=PO2l⋅PB=POl⋅POPB=sin∠PA1O⋅sin∠PBO ①
易知∠PA1O是侧棱与底面所成的角,又由OB⊥A1An,PB⊥A1An知∠PBO是侧面与底面所成的角.于是∠PA1O=α,∠PBO=β.
从而由①得1ni=1ncos∠AiPB与sinα⋅sinβ相等.
4．【2020年甘肃预赛】如图1,在直角梯形ABCD中,AD//BC,∠BAD=π2,AB=BC=1,AD= 2,E为AD的中点,O 为AC与BE的交点.将△ABE 沿BE折起到△A1BE 的位置,如图2.
(1) 证明：CD⊥平面A1OC ;
(2)若平面A1BE⊥ 平面BCDE,求二面角B-A1C-D 的正弦值.
【答案】(1)证明见解析；(2) 33.
【解析】(1) 在图1中,因为AB=BC=1,AD =2,E 为AD的中点,∠BAD=π2 ,所以,BE⊥AC ,即在图2中,BE⊥OA1,BE⊥OC ,且A1O 与OC交于点O.从而,BE⊥ 平面A1OC.
又AD//BC,BC=12AD,E 为AD的中点,则BC//ED .
于是,四边形BCDE为平行四边形.故CD//BE .从而,CD⊥ 平面A1OC.
(2)由平面A1BE⊥ 平面BCDE,结合(1) ,知BE⊥OA1,BE⊥OC.
于是,∠A1OC 为二面角A1-BE-C 的平面角.
从而,∠A1OC=π2 .
如图6,以O 为原点建立空间直角坐标系.

由A1B=A1E =BC=ED=1,BC //ED ,知
B22,0,0,E-22,0,0,A10,0,22 ,C0,22,0.
则BC=-22,22,0 ,A1C=0,22,-22 ,CD=BE=(-2,0,0) .
设平面A1BC 的法向量n1=x1,y1,z1 ,
平面A1CD 的法向量n2=x2,y2,z2.
则n1⋅BC=0,n1⋅A1C=0⇒-x1+y1=0,y1-z1=0
取n1=(1,1,1);
n2⋅CD=0,n2⋅A1C=0⇒x2=0y2-z2=0
取n2=(0,1,1) .
故∣cos1=23×2=63 .
设二面角B-A1C-D 为θ. 则
sinθ=33 ,
即二面角B-A1C-D 的正弦值为33 .
5．【2019年内蒙古预赛】1863年法国 Prouhet数学家将三角形的九点圆定理类比推广到垂心四面体中,由此产生 Prouhet球面的概念,后又得到广义 Prouhet球面的定义如下(注:以点O的球心,以R为半径的球面表示为S(O,R).设任意一个四面体A1A2A3A4的外接球面为S(O,R),对于空间中异于点O任意一个点H,以线段OH的第二个三等分点P为球心,R3为半径的球面称为四面体A1A2A3A4的广义球面记为SP,R3,其中球心P满足OP=23OH.
根据上述定义证明如下结论:设四面体A1A2A3A4的外接球面为S(O,R),对于空间中异于点O的任意一个点H,记线段OH的中点为G,连接AiG并延长至G,使得GGi=13AiG,i=1,2,3,4.
【答案】证明见解析
【解析】∵OP=23OH,OG=12OH, ∴OP=43OG,BGBOG+GP=43OG
∴GP=13OG，而GGi=13AiG,i=1,2,3,4.
∴ΔAiGO~ΔGiGP，即PGi=13R, i=1,2,3,4.
∴球面SP,R3必经过点Gi.
6．【2018年湖南预赛】在四面体ABCD中，过棱AB的上一点E作平行于AD，BC的平面分别交四面体的棱BD，DC，CA于点F，G，H

（1）求证：截面EFGH为平行四边形
（2）若P、Q在线段BD、AC上，DPBD=AQAC=14，且P、F不重合，证明：PQ∥截面EFGH
【答案】（1）见解析；（2）见解析
【解析】
（1）证明：∵AD∥平面EFGH，平面ADB∩平面EHGH=EF，AD⊂平面ABD，
∴AD∥EF ∵AD∥平面EHGH，平面ADC∩平面EHGH=GH，AD⊂平面ADC，. ∴AD∥GH
由平行公理可得EF∥GH
同理可得EH∥FG

∴四边形EFGH为平行四边形.
（2）如图在CD上取点M，使DPBD=DMDC=14，连接MQ
则PM∥BC∥FG，AQAC=DMDC=14，则QM∥AD∥HG
PM∩QM=M∴平面PMQ∥平面EHGH
∵PQ⊂平面PMQ
∴PQ∥截面EFGH
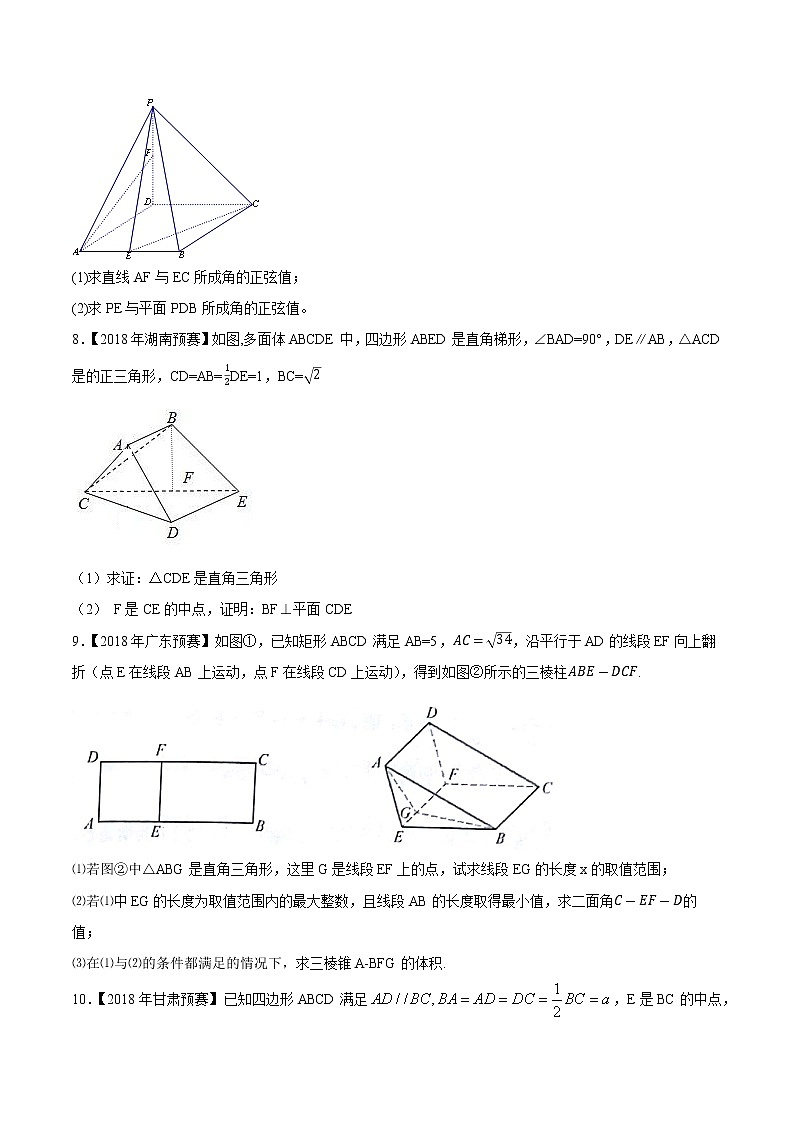
7．【2018年湖南预赛】如图,在四棱锥P−ABCD中,底面ABCD是菱形,∠DAB=60°，PD⊥平面ABCD，PD=AD=1，点E，F分别为AB和PD中点。

(1)求直线AF与EC所成角的正弦值；
(2)求PE与平面PDB所成角的正弦值。
【答案】（1）147；（2）2114
【解析】
(1)作FM∥CD交PC于M.
∵点F为PD中点,∴FM=12CD.

∴AE=12AB=FM，
∴AEMF为平行四边形,∴AF∥EM，
∠MEC为直线AF与EC所成角或其补角。
EM=AF=52，MC=22，EC=72，∴ΔMEC为RtΔMEC
sin∠MEC=MCEC=2272=147
(2)连接AC，BD交于O，连接EG
∵点E，O分别为AB和AC中点。
∴AO∥EG，
∵AC⊥平面PBD，
∴EG⊥平面PBD，
根据直线与平面所成角的定义可得：∠EPG为PE与平面PDB所成角，

Rt△EGP中,AO=32，EG=34，
DE=32，PE=12+(34)2=72，
∴sin∠EPG=3472=2114
8．【2018年湖南预赛】如图,多面体ABCDE中，四边形ABED是直角梯形，∠BAD=90°，DE∥AB，△ACD是的正三角形，CD=AB=12DE=1，BC=2

（1）求证：△CDE是直角三角形
（2） F是CE的中点，证明：BF⊥平面CDE
【答案】（1）见解析；（2）见解析
【解析】
（1）证明：∵∠BAD=90°∴AB⊥AD
△ACD是的正三角形，CD=AB=1，BC=2，

∴△ABC是直角三角形，AB⊥AC
∴AB⊥平面ACD
∵DE∥AB
∴DE⊥平面ACD
∴△CDE是直角三角形
(2)证明:取CD中点M，连接AM、MF.
∵F是CE的中点
∴AMFB是平行四边形
∴MF∥AB，AM∥BF
∴MF⊥平面ACD
∵MF在平面ECD内
∴平面CDE⊥平面ACD
∵△ACD是的正三角形，M是CD中点
∴AM⊥CD
平面CED∩平面ACD=CD,∴AM⊥面CDE，
∵AM∥BF，
∴BF⊥平面CDE
9．【2018年广东预赛】如图①，已知矩形ABCD满足AB=5，AC=34，沿平行于AD的线段EF向上翻折（点E在线段AB上运动，点F在线段CD上运动），得到如图②所示的三棱柱ABE-DCF.

⑴若图②中△ABG是直角三角形，这里G是线段EF上的点，试求线段EG的长度x的取值范围；
⑵若⑴中EG的长度为取值范围内的最大整数，且线段AB的长度取得最小值，求二面角C-EF-D的值；
⑶在⑴与⑵的条件都满足的情况下，求三棱锥A-BFG的体积.
【答案】（1）0,2.5（2）∠AEB=π-arccos825（3）3561-8224
【解析】
⑴由题设条件可知△AEG、△BEG均为直角三角形，
因此AG2=AE2+x2，BG2=BE2+x2.
由余弦定理AB2=AE2+BE2-2AE⋅BEcos∠AEB.
于是2x2+AE2+BE2=AB2=AE2+BE2-2AE⋅BEcos∠AEB.
x2=-AE⋅BEcos∠AEB