初中数学人教版八年级下册第十七章 勾股定理综合与测试单元测试课后测评

这是一份初中数学人教版八年级下册第十七章 勾股定理综合与测试单元测试课后测评，共9页。
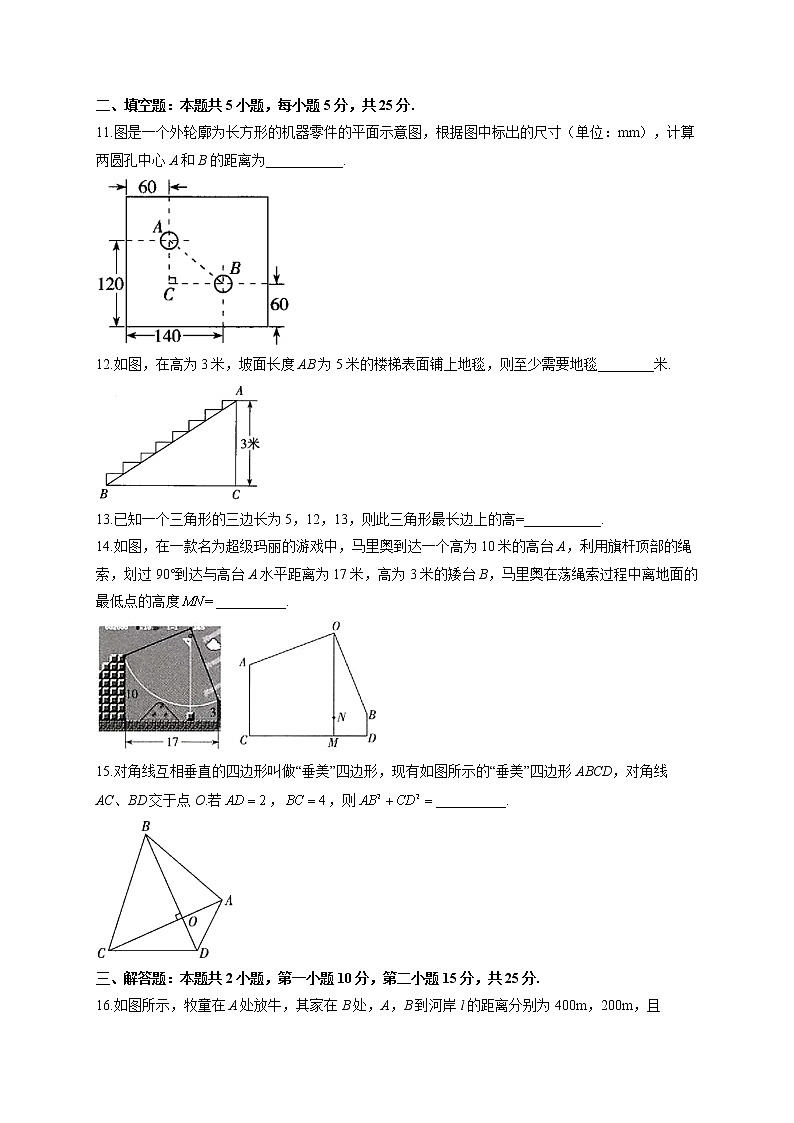
第十七章 勾股定理B卷 能力提升—2021-2022学年人教版八年级下册数学单元测试AB卷【满分：100分】一、选择题：本题共10小题，每小题5分，共50分.1.一个三角形的两边长为4和5，要使该三角形为直角三角形，则第三条边长为(   )A.3 B. C.或3 D.92.一辆拖拉机沿着公路l以20km/h的速度前行，幼儿园R距离公路l大约3km，拖拉机产生的噪音能够影响周围5km的区域，则幼儿园学生受拖拉机噪音影响持续的时间约为(   )A.0.4h B.0.8h C.1.2h D.1.5h3.已知M、N是线段AB上的两点，，，以点A为圆心，AN长为半径画弧；再以点B为圆心，BM长为半径画弧，两弧交于点C，连接AC，BC，则一定是(   )A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形4.在《算法统宗》中有一道“荡秋千”的问题：“平地秋千未起，踏板一尺离地.送行二步与人齐，五尺人高曾记.仕女佳人争蹴，终朝笑语欢嬉.良工高士素好奇，算出索长有几.”此问题可理解为如图，有一架秋千，当它静止时，踏板离地的距离AB为1尺.将它往前水平推送10尺时（即尺），秋千的踏板就和身高5尺的人一样高，即尺.若运动过程中秋千的绳索始终拉得很直，则绳索OA长为(   )A.13.5尺 B.14尺 C.14.5尺 D.15尺5.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？译文：有一块三角形沙田，三边长分别为5里，12里，13里，问这块沙田面积有多大？题中的“里”是我国市制长度单位，1里=500米，则该沙田的面积为(   )A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方千米6.下列条件：①，②，③，④，⑤中，能确定是直角三角形的有(   )A.2个 B.3个 C.4个 D.5个7.如图，中，，，，把沿直线BC向右平移3个单位长度得到，则四边形的面积是(   )A.15 B.18 C.20 D.228.如图，在直角中，，，，AB边的垂直平分线DE交AB于点D，交BC于点E，连接AE，则的周长为(   )A.16 B.15 C.14 D.139.如图，已知，，，，若点P到AC的距离为5，则点P在四边形ABCD边上的个数为(   )A.0 B.2 C.3 D.410.如图，中，，，，AD为的角平分线，则CD的长度为(   )A.1 B. C. D.二、填空题：本题共5小题，每小题5分，共25分.11.图是一个外轮廓为长方形的机器零件的平面示意图，根据图中标出的尺寸（单位：mm），计算两圆孔中心A和B的距离为___________.12.如图，在高为3米，坡面长度AB为5米的楼梯表面铺上地毯，则至少需要地毯________米.13.已知一个三角形的三边长为5，12，13，则此三角形最长边上的高=___________.14.如图，在一款名为超级玛丽的游戏中，马里奥到达一个高为10米的高台A，利用旗杆顶部的绳索，划过90°到达与高台A水平距离为17米，高为3米的矮台B，马里奥在荡绳索过程中离地面的最低点的高度__________.15.对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD，对角线AC、BD交于点O.若，，则__________.三、解答题：本题共2小题，第一小题10分，第二小题15分，共25分.16.如图所示，牧童在A处放牛，其家在B处，A，B到河岸l的距离分别为400m，200m，且m，牧童从A处把牛牵到河边饮水后再回家.问在何处饮水牧童所走的路程最短？最短路程是多少？17.如图，在平面直角坐标系中，点，.（1）若点P在x轴上，求的最小值.（2）若点Q在x轴上，且的值最大，求点Q的坐标.
答案以及解析1.答案：C解析：当长为4和5的两边都是直角边时，斜边长是；当长是5的边是斜边时，第二边长是.所以第三边长为或3.故选C.2.答案：A解析：如图所示，过点R作，由题意可得，km，km，在直角中，由勾股定理得km，由题意得km，则幼儿园学生受拖拉机噪音影响持续的时间约为h.故选A.3.答案：B解析：如图所示，，，，，是直角三角形，且，故选B.4.答案：C解析：设绳索OA长为x尺，则，解得.故绳索OA长为14.5尺.故选C.5.答案：A解析：将里换算为米，则三角形沙田的三边长分别为2.5千米，6千米，6.5千米.因为，所以该三角形沙田为直角三角形，且直角边长分别为2.5千米和6千米，所以（平方千米）.故选A.6.答案：C解析：①时，，是直角三角形；②，是直角三角形；③，设，，，，是直角三角形；④时，，是锐角三角形；⑤，，是直角三角形.故能确定是直角三角形的有4个.故选C.7.答案：A解析：如图，把沿直线BC向右平移3个单位长度得到，，.在中，，，，.，四边形是梯形，四边形的面积为，故选A.8.答案：A解析：因为在直角中，，，，所以，所以，因为DE垂直平分AB，所以，所以的周长.故选A.9.答案：A解析：如图，过点B，D分别作，，垂足分别为E，F.在中，由勾股定理，得，所以.再由，可得.由且，得，由勾股定理，得，故.又因为，所以到直线AC的距离为5的两条平行线与四边形ABCD的边没有交点.故选A.10.答案：D解析：，，，，.过D作于P.AD平分，.又，，.在与中，，，，.设，则，.在中，，，即，解得，.11.答案：100mm解析：在中，（mm），（mm），，mm，两圆孔中心A和B的距离为100mm.12.答案：7解析：将楼梯表面向下和向右平移，则地毯的总长=两直角边长的和，已知米，米，且在直角中，，AB为斜边，则米，则米，即至少需要地毯7米.13.答案：解析：因为，，所以，所以此三角形为直角三角形，设最长边上的高为x，则，所以.14.答案：2米解析：如图，作，，，，在和中，，，，，即（m），m.（m），m，m，m，易知m，又m，（m）.马里奥在荡绳索过程中离地面的最低点的高度MN为2米.15.答案：20解析：，，由勾股定理得，，，，，，.故答案为20.16.答案：如图所示，作点A关于直线l的对称点G，连接GB交CD于点E，连接AE，则在E处饮水牧童所走的路程最短.理由：在直线CD上任意取一异于点E的点I，连接AI，BI，GI.点G，A关于直线I对称，，，，.由“两点之间线段最短”和“三角形任意两边之和大于第三边”可得，在E处饮水牧童所走路程最短，最短路程为GB的长.过点G作BD的垂线，与BD的延长线交于点H.m，m，在中，由勾股定理，得.m，即最短路程为1000m.17.答案：（1）如图，作点A关于x轴的对称点C，则，连接BC，交x轴于点P，则，此时有最小值，过点B作轴，过点C作于点D.，，，，.在中，由勾股定理得.的最小值为.（2），，A,B两点都在第一象限的角平分线上，即A,B,O点在同一条直线上，.设Q点是x轴上异于原点O的任意一点，连接QA,QB，在中，由三角形的三边关系，得.Q点具有任意性，当且仅当点Q和原点O重合时，，当点Q和原点O重合时，有最大值，此时.