2020-2021学年北京人大附中八年级（下）期末数学模拟练习试卷（8）

这是一份2020-2021学年北京人大附中八年级（下）期末数学模拟练习试卷（8），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2020-2021学年北京人大附中八年级（下）期末数学模拟练习试卷（8）
一、选择题（每题3分，共30分）
1．（3分）下列命题中是真命题的是（　　）
A．同位角相等
B．有两边及一角分别相等的两个三角形全等
C．两组对边分别相等的四边形是平行四边形
D．对角线相等的四边形是平行四边形
2．（3分）下列命题是真命题的是（　　）
A．π是单项式
B．三角形的一个外角大于任何一个内角
C．两点之间，直线最短
D．同位角相等
3．（3分）昆明市高新区某厂今年新招聘一批员工，他们中同文化程度的人数见下表：关于这组文化程度的人数数据，以下说法正确的是（　　）
文化程度
高中
大专
本科
硕士
博士
人数
9
17
20
9
5
A．众数是20 B．中位数是17 C．平均数是12 D．方差是26
4．（3分）射击训练中，甲、乙、丙、丁四人每人射击10次，平均环数均为8.7环，方差分别为S甲2＝0.51，S乙2＝0.62，S丙2＝0.48，S丁2＝0.45，则四人中成绩最稳定的是（　　）
A．甲 B．乙 C．丙 D．丁
5．（3分）给出下列四个命题
（1）一组对边平行的四边形是平行四边形
（2）一条对角线平分一个内角的平行四边形是菱形
（3）两条对角线互相垂直的矩形是正方形
（4）顺次连接四边形四边中点所得的四边形是平行四边形．
其中正确命题的个数为（　　）
A．1个 B．2个 C．3个 D．4个
6．（3分）关于函数y＝﹣x+3的图象，下列结论错误的是（　　）
A．图象经过一、二、四象限
B．与y轴的交点坐标为（3，0）
C．y随x的增大而减小
D．图象与两坐标轴相交所形成的直角三角形的面积为
7．（3分）在平面直角坐标系中，已知定点A（﹣，3）和动点P（a，a），则PA的最小值为（　　）
A．2 B．4 C．2 D．4
8．（3分）小军自制的匀速直线运动遥控车模型甲、乙两车同时分别从A、B出发，沿直线轨道同时到达C处，已知乙的速度是甲的速度的1.5倍，甲、乙两遥控车与A处的距离d1、d2（米）与时间t（分钟）的函数关系如图所示，则下列结论中：
①AC的距离为120米；
②乙的速度为60米/分；
③a的值为；
④若甲、乙两遥控车的距离不少于10米时，两车信号不会产生相互干扰，则两车信号不会产生相互干扰的t的取值范围是0≤t≤，
其中正确的有（　　）个

A．1 B．2 C．3 D．4
9．（3分）点A（x1，y1），B（x2，y2）在正比例函数y＝﹣3x的图象上，若x1+x2＝﹣5，则y1+y2的值是（　　）
A．15 B．8 C．﹣15 D．﹣8
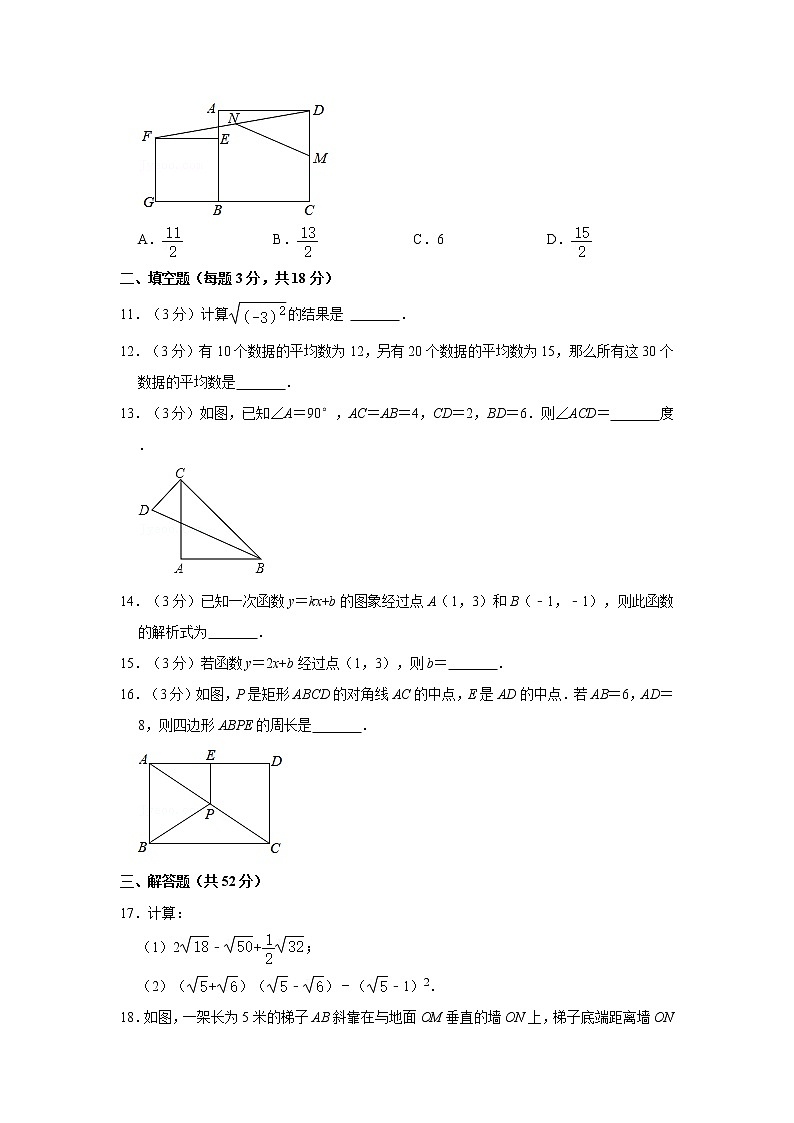
10．（3分）如图，已知点E在正方形ABCD的边AB上，以BE为边向正方形ABCD外部作正方形BEFG，连接DF，M，N分别是DC，DF的中点，连接MN．若AB＝7，BE＝5，则MN＝（　　）

A． B． C．6 D．
二、填空题（每题3分，共18分）
11．（3分）计算的结果是 　 　．
12．（3分）有10个数据的平均数为12，另有20个数据的平均数为15，那么所有这30个数据的平均数是　 　．
13．（3分）如图，已知∠A＝90°，AC＝AB＝4，CD＝2，BD＝6．则∠ACD＝　 　度．

14．（3分）已知一次函数y＝kx+b的图象经过点A（1，3）和B（﹣1，﹣1），则此函数的解析式为　 　．
15．（3分）若函数y＝2x+b经过点（1，3），则b＝　 　．
16．（3分）如图，P是矩形ABCD的对角线AC的中点，E是AD的中点．若AB＝6，AD＝8，则四边形ABPE的周长是　 　．

三、解答题（共52分）
17．计算：
（1）2﹣+；
（2）（+）（﹣）﹣（﹣1）2．
18．如图，一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上，梯子底端距离墙ON有3米．
（1）求梯子顶端与地面的距离OA的长．
（2）若梯子顶点A下滑1米到C点，求梯子的底端向右滑到D的距离．

19．学校为了解全校学生参加社会实践活动情况，随机调查了部分学生一学期参加社会实践活动的时间（单位：天），并用得到的数据绘制了统计图（1）和图 （2）．请根据图中提供的信息，回答下列问题：

（Ⅰ）本次随机调查的学生人数是　 　，图（1）中m的值是　 　；
（Ⅱ）求调查获取的学生社会实践活动时间样本数据的众数、中位数和平均数；
（Ⅲ）该校有480名学生，根据获取的社会实践活动时间样本数据，估计该校一学期社会实践活动时间大于10天的学生人数．
20．已知，如图，在△ABC中，AB＝AC，AD是BC边的中线，过点A作BC的平行线，过点B作AD的平行线，两线交于点E，连接DE交AB于点O．
（1）求证：四边形ADBE是矩形；
（2）若BC＝8，AO＝，求四边形AEBC的面积．

21．（9分）如图反映的过程是：小明从家出发去菜地浇水，又去玉米地锄草，然后回家．其中x表示时间，y表示小明离他家的距离，小明家，菜地，玉米地在同一直线上．根据图象回答下列问题：
（1）菜地离小明家多远？小明走到菜地用了多长时间？小明给菜地浇水用了多长时间？
（2）菜地离玉米地多远？小明从菜地到玉米地用了多长时间？
（3）小明给玉米地锄草用了多长时间？
（4）玉米地离小明家多远？小明从玉米地走回家的平均速度是多少？

22．某游泳馆普通票价20元/张，暑假为了促销，新推出两种优惠卡：
①金卡售价600元/张，每次凭卡不再收费．
②银卡售价150元/张，每次凭卡另收10元．
暑假普通票正常出售，两种优惠卡仅限暑假使用，不限次数．设游泳x次时，所需总费用为y元
（1）分别写出选择银卡、普通票消费时，y与x之间的函数关系式；
（2）在同一坐标系中，若三种消费方式对应的函数图象如图所示，请求出点A、B、C的坐标；
（3）请根据函数图象，直接写出选择哪种消费方式更合算．


2020-2021学年北京人大附中八年级（下）期末数学模拟练习试卷（8）
参考答案与试题解析
一、选择题（每题3分，共30分）
1．（3分）下列命题中是真命题的是（　　）
A．同位角相等
B．有两边及一角分别相等的两个三角形全等
C．两组对边分别相等的四边形是平行四边形
D．对角线相等的四边形是平行四边形
【分析】利用平行线的性质、全等三角形的判定方法及平行四边形的判定方法分别判断后，即可确定正确的选项．
【解答】解：A、两直线平行，同位角相等，故原命题错误，是假命题，不符合题意；
B、有两边及夹角分别相等的两个三角形全等，故原命题错误，是假命题，不符合题意；
C、两组对边分别相等的四边形是平行四边形，正确，是真命题，符合题意；
D、对角线互相平分的四边形是平行四边形，故原命题错误，是假命题，不符合题意，
故选：C．
【点评】考查了命题与定理的知识，解题的关键是了解平行线的性质、全等三角形的判定方法及平行四边形的判定方法等知识，难度不大．
2．（3分）下列命题是真命题的是（　　）
A．π是单项式
B．三角形的一个外角大于任何一个内角
C．两点之间，直线最短
D．同位角相等
【分析】根据单项式、三角形外角性质、线段公理、平行线性质解答即可．
【解答】解：A、π是单项式，是真命题；
B、三角形的一个外角大于任何一个与之不相邻的内角，是假命题；
C、两点之间，线段最短，是假命题；
D、两直线平行，同位角相等，是假命题；
故选：A．
【点评】本题考查了命题与定理：命题写成“如果…，那么…”的形式，这时，“如果”后面接的部分是题设，“那么”后面解的部分是结论．命题的“真”“假”是就命题的内容而言．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．
3．（3分）昆明市高新区某厂今年新招聘一批员工，他们中同文化程度的人数见下表：关于这组文化程度的人数数据，以下说法正确的是（　　）
文化程度
高中
大专
本科
硕士
博士
人数
9
17
20
9
5
A．众数是20 B．中位数是17 C．平均数是12 D．方差是26
【分析】根据众数、中位数、平均数以及方差的概念求解．
【解答】解：A、这组数据中9出现的次数最多，众数为9，故本选项错误；
B、从小到大排列后，9在中间的位置，即9是中位数，故本选项错误；
C、平均数＝＝12，故本选项正确；
D、方差S2＝，故本选项错误；
故选：C．
【点评】本题考查了中位数、平均数、众数的知识，解答本题的关键是掌握各知识点的概念．
4．（3分）射击训练中，甲、乙、丙、丁四人每人射击10次，平均环数均为8.7环，方差分别为S甲2＝0.51，S乙2＝0.62，S丙2＝0.48，S丁2＝0.45，则四人中成绩最稳定的是（　　）
A．甲 B．乙 C．丙 D．丁
【分析】根据方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好可得答案．
【解答】解：∵0.45＜0.51＜0.62，
∴丁成绩最稳定，
故选：D．
【点评】此题主要考查了方差，关键是掌握方差越小，稳定性越大．
5．（3分）给出下列四个命题
（1）一组对边平行的四边形是平行四边形
（2）一条对角线平分一个内角的平行四边形是菱形
（3）两条对角线互相垂直的矩形是正方形
（4）顺次连接四边形四边中点所得的四边形是平行四边形．
其中正确命题的个数为（　　）
A．1个 B．2个 C．3个 D．4个
【分析】根据平行四边形的判定方法对（1）进行判断；根据菱形的判定方法对（2）进行判断；根据正方形的判定方法对（3）进行判断；利用三角形中位线的性质和平行四边形的判定方法对（4）进行判断．
【解答】解：两组对边分别平行的四边形是平行四边形，所以（1）为假命题；
一条对角线平分一个内角的平行四边形是菱形，所以（2）为真命题；
两条对角线互相垂直的矩形是正方形，所以（3）为真命题；
顺次连接四边形四边中点所得的四边形是平行四边形，所以（4）为真命题．
故选：C．
【点评】本题考查了命题与定理：命题写成“如果…，那么…”的形式，这时，“如果”后面接的部分是题设，“那么”后面解的部分是结论．命题的“真”“假”是就命题的内容而言．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．
6．（3分）关于函数y＝﹣x+3的图象，下列结论错误的是（　　）
A．图象经过一、二、四象限
B．与y轴的交点坐标为（3，0）
C．y随x的增大而减小
D．图象与两坐标轴相交所形成的直角三角形的面积为
【分析】根据一次函数的性质对各选项进行逐一判断即可．
【解答】解：A、由k＝﹣1＜0，b＝3＞0知，该图象经过第一、二、四象限，故本选项不符合题意．
B、当x＝0时，y＝3，则图象与y轴的交点坐标为（0，3），故本选项符合题意．
C、由k＝﹣1＜0知，y的值随x的增大而减小，故本选项不符合题意．
D、图象与两坐标轴相交所形成的直角三角形的面积为：＝，故本选项不符合题意．
故选：B．
【点评】本题考查的是一次函数的性质，熟知一次函数y＝kx+b（k≠0），当k＞0，y随x的增大而增大，函数从左到右上升；k＜0，y随x的增大而减小，函数从左到右下降是解答此题的关键．
7．（3分）在平面直角坐标系中，已知定点A（﹣，3）和动点P（a，a），则PA的最小值为（　　）
A．2 B．4 C．2 D．4
【分析】根据勾股定理、两点间的距离公式得到关于a的代数式，根据配方法、偶次方的非负性解答．
【解答】解：PA＝
＝
＝，
∴PA的最小值为＝4，
故选：B．
【点评】本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2＝c2．
8．（3分）小军自制的匀速直线运动遥控车模型甲、乙两车同时分别从A、B出发，沿直线轨道同时到达C处，已知乙的速度是甲的速度的1.5倍，甲、乙两遥控车与A处的距离d1、d2（米）与时间t（分钟）的函数关系如图所示，则下列结论中：
①AC的距离为120米；
②乙的速度为60米/分；
③a的值为；
④若甲、乙两遥控车的距离不少于10米时，两车信号不会产生相互干扰，则两车信号不会产生相互干扰的t的取值范围是0≤t≤，
其中正确的有（　　）个

A．1 B．2 C．3 D．4
【分析】根据题意和函数图象中的数据可以判断各个小题中的结论是否成立，从而可以解答本题．
【解答】解：由图可得，
AC的距离为120米，故①正确；
乙的速度为：（60+120）÷3＝60米/分，故②正确；
a的值为：60÷60＝1，故③错误；
令[60+（120÷3）t]﹣60t≥10，得t≤，
即若甲、乙两遥控车的距离不少于10米时，两车信号不会产生相互干扰，则两车信号不会产生相互干扰的t的取值范围是0≤t≤，故④正确；
故选：C．
【点评】本题考查一次函数的应用，解答本题的关键是明确题意，利用一次函数的性质和数形结合的思想解答．
9．（3分）点A（x1，y1），B（x2，y2）在正比例函数y＝﹣3x的图象上，若x1+x2＝﹣5，则y1+y2的值是（　　）
A．15 B．8 C．﹣15 D．﹣8
【分析】利用一次函数图象上点的坐标特征可得出y1＝﹣3x1，y2＝﹣3x2，结合x1+x2＝﹣5即可求出y1+y2的值．
【解答】解：∵A（x1，y1），B（x2，y2）在正比例函数y＝﹣3x的图象上，
∴y1＝﹣3x1，y2＝﹣3x2，
又∵x1+x2＝﹣5，
∴y1+y2＝﹣3（x1+x2）＝﹣3×（﹣5）＝15．
故选：A．
【点评】本题考查了一次函数图象上点的坐标特征，牢记直线上任意一点的坐标都满足函数关系式y＝kx+b是解题的关键．
10．（3分）如图，已知点E在正方形ABCD的边AB上，以BE为边向正方形ABCD外部作正方形BEFG，连接DF，M，N分别是DC，DF的中点，连接MN．若AB＝7，BE＝5，则MN＝（　　）

A． B． C．6 D．
【分析】连接CF，则MN为△DCF的中位线，根据勾股定理求出CF长，即可求出MN的长．
【解答】解：连接CF，

∵正方形ABCD和正方形BEFG中，AB＝7，BE＝5，
∴GF＝GB＝5，BC＝7，
∴GC＝GB+BC＝5+7＝12，
∴CF＝＝＝13，
∵M，N分别是DC，DF的中点，
∴MN＝CF＝，
故选：B．
【点评】本题考查了正方形的性质，三角形的中位线定理、勾股定理等知识点，构造基本图形是解题的关键．
二、填空题（每题3分，共18分）
11．（3分）计算的结果是 　3　．
【分析】根据二次根式的性质解答．
【解答】解：＝＝3．
故答案为：3．
【点评】本题考查的是二次根式的化简，掌握二次根式的性质是解题的关键．
12．（3分）有10个数据的平均数为12，另有20个数据的平均数为15，那么所有这30个数据的平均数是　14　．
【分析】根据加权平均数的定义计算．
【解答】解：所有这30个数据的平均数＝＝14．
故答案为14．
【点评】本题考查了加权平均数：若n个数x1，x2，x3，…，xn的权分别是w1，w2，w3，…，wn，则（x1w1+x2w2+…+xnwn）÷（w1+w2+…+wn）叫做这n个数的加权平均数．
13．（3分）如图，已知∠A＝90°，AC＝AB＝4，CD＝2，BD＝6．则∠ACD＝　45　度．

【分析】根据勾股定理求出BC，根据勾股定理的逆定理得到∠BCD＝90°，结合图形计算，得到答案．
【解答】解：∵∠A＝90°，AC＝AB＝4，
∴∠ACB＝∠ABC＝45°，
在Rt△ABC中，BC＝＝4，
CD2+BC2＝22+（4）2＝36，BD2＝62＝36，
∴CD2+BC2＝BD2，
∴∠BCD＝90°，
∴∠ACD＝45°，
故答案为：45．
【点评】本题考查的是勾股定理和勾股定理的逆定理，如果三角形的三边长a，b，c满足a2+b2＝c2，那么这个三角形就是直角三角形．
14．（3分）已知一次函数y＝kx+b的图象经过点A（1，3）和B（﹣1，﹣1），则此函数的解析式为　y＝2x+1　．
【分析】把A、B两点的坐标代入函数解析式，就可得到一个关于k、b的方程组，解方程组即可求出k、b的值，从而得到解析式．
【解答】解：由题意可得方程组，
解得，
则此函数的解析式为：y＝2x+1．
【点评】本题要注意利用一次函数的特点，根据已知坐标列出方程组，求出未知数．
15．（3分）若函数y＝2x+b经过点（1，3），则b＝　1　．
【分析】由于函数y＝2x+b经过点（1，3），故可将点的坐标代入函数解析式，求出b的值．
【解答】解：将点（1，3）代入y＝2x+b得
3＝2+b，
解得b＝1．
故答案为：1．
【点评】本题考查了一次函数图象上点的坐标特征，要知道函数图象上的点符合函数解析式．
16．（3分）如图，P是矩形ABCD的对角线AC的中点，E是AD的中点．若AB＝6，AD＝8，则四边形ABPE的周长是　18　．

【分析】由矩形的性质得出∠ABC＝90°，CD＝AB＝6，BC＝AD＝8，由勾股定理求出AC，由直角三角形斜边上的中线性质得出BP，证明PE是△ACD的中位线，由三角形中位线定理得出PE＝CD＝3，四边形ABPE的周长＝AB+BP+PE+AE，即可得出结果．
【解答】解：∵四边形ABCD是矩形，
∴∠ABC＝90°，CD＝AB＝6，BC＝AD＝8，
∴AC＝＝10，
∴BP＝AC＝5，
∵P是矩形ABCD的对角线AC的中点，E是AD的中点，
∴AE＝AD＝4，PE是△ACD的中位线，
∴PE＝CD＝3，
∴四边形ABPE的周长＝AB+BP+PE+AE＝6+5+3+4＝18；
故答案为：18．
【点评】本题考查了矩形的性质、勾股定理、直角三角形斜边上的中线性质、三角形中位线定理；熟练掌握矩形的性质，并能进行推理论证与计算是解决问题的关键．
三、解答题（共52分）
17．计算：
（1）2﹣+；
（2）（+）（﹣）﹣（﹣1）2．
【分析】（1）先化为最简二次根式，然后根据二次根式的运算法则即可求出答案．
（2）根据完全平方公式以及平方差公式即可求出答案．
【解答】解：（1）原式＝6﹣5+2
＝3．
（2）原式＝5﹣6﹣（5﹣2+1）
＝﹣1﹣（6﹣2）
＝﹣1﹣6+2
＝﹣7+2．
【点评】本题考查二次根式的运算，解题的关键是熟练运用二次根式的运算法则，本题属于基础题型．
18．如图，一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上，梯子底端距离墙ON有3米．
（1）求梯子顶端与地面的距离OA的长．
（2）若梯子顶点A下滑1米到C点，求梯子的底端向右滑到D的距离．

【分析】（1）已知直角三角形的斜边和一条直角边，可以运用勾股定理计算另一条直角边；
（2）在直角三角形OCD中，已知斜边仍然是5，OC＝4﹣1＝3，再根据勾股定理求得OD的长即可．
【解答】解：（1）AO＝＝4米；

（2）OD＝＝4米，BD＝OD﹣OB＝4﹣3＝1米．
【点评】能够运用数学知识解决实际生活中的问题，考查了勾股定理的应用．
19．学校为了解全校学生参加社会实践活动情况，随机调查了部分学生一学期参加社会实践活动的时间（单位：天），并用得到的数据绘制了统计图（1）和图 （2）．请根据图中提供的信息，回答下列问题：

（Ⅰ）本次随机调查的学生人数是　40　，图（1）中m的值是　20　；
（Ⅱ）求调查获取的学生社会实践活动时间样本数据的众数、中位数和平均数；
（Ⅲ）该校有480名学生，根据获取的社会实践活动时间样本数据，估计该校一学期社会实践活动时间大于10天的学生人数．
【分析】（Ⅰ）依据条形统计图中的数据，即可得到本次随机调查的学生人数以及图（1）中m的值；
（Ⅱ）依据条形统计图中的数据，即可得出众数、中位数和平均数；
（Ⅲ）在统计的这组学生参加社会实践活动时间的样本数据中，社会实践活动时间大于10天的学生人数占60%，即可估计该校一学期社会实践活动时间大于10天的学生人数．
【解答】解：（Ⅰ）本次随机调查的学生人数是4+12+10+8+6＝40，
m%＝×100%＝20%．
故答案为：40，20；
（Ⅱ）观察条形统计图，
∵在这组数据中，10出现了12次，出现的次数最多，
∴这组数据的众数为10．
∵将这组数据按从小到大的顺序排列，其中处于中间的两个数都是11，
有，
∴这组数据的中位数为11．
∵，
∴这组数据的平均数是11．
（Ⅲ）∵在统计的这组学生参加社会实践活动时间的样本数据中，社会实践活动时间大于10天的学生人数占60%，
∴估计该校480名学生中，参加社会实践活动时间大于10天的学生人数约占60%，有480×60%＝288．
∴参加社会实践活动时间大于10天的学生人数约为288．
【点评】本题考查的是统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．
20．已知，如图，在△ABC中，AB＝AC，AD是BC边的中线，过点A作BC的平行线，过点B作AD的平行线，两线交于点E，连接DE交AB于点O．
（1）求证：四边形ADBE是矩形；
（2）若BC＝8，AO＝，求四边形AEBC的面积．

【分析】（1）只要证明四边形ADBE是平行四边形，且∠ADB＝90°，即可；
（2）求BD、AB，利用三角形面积公式可得S四边形AEBC＝S△ABC+S△ABE．
【解答】解：（1）∵AE∥BC，BE∥AD，
∴四边形ADBE是平行四边形，
∵AB＝AC，AD是BC边的中线，
∴AD⊥BC，
即∠ADB＝90°．
∴四边形ADBE为矩形．
（2）∵在矩形ADBE中，AO＝，

∴DE＝AB＝5，
∵D是BC的中点，
∴AE＝DB＝4，
∵∠ADB＝90°，
根据勾股定理，
∴S△ABC＝×BC×AD＝×8×3＝12，
∴S△ABE＝×AE×BE＝×4×3＝6，
∴S四边形AEBC＝S△ABC+S△ABE＝12+6＝18，
即S四边形AEBC为18．
【点评】本题考查矩形的判定和性质、等腰三角形的性质，平行四边形的判定和性质等知识，解题的关键是熟练掌握矩形的判定方法，属于中考常考题型．
21．（9分）如图反映的过程是：小明从家出发去菜地浇水，又去玉米地锄草，然后回家．其中x表示时间，y表示小明离他家的距离，小明家，菜地，玉米地在同一直线上．根据图象回答下列问题：
（1）菜地离小明家多远？小明走到菜地用了多长时间？小明给菜地浇水用了多长时间？
（2）菜地离玉米地多远？小明从菜地到玉米地用了多长时间？
（3）小明给玉米地锄草用了多长时间？
（4）玉米地离小明家多远？小明从玉米地走回家的平均速度是多少？

【分析】观察函数图象得到小明用15分钟从家去菜地，浇水用了10分钟，又去离家2千米的玉米地，锄草用了18分钟，然后用了25分钟回家．
【解答】解：由图象得：
（1）菜地离小明家1.1千米，小明从家到菜地用了15分钟，小明给菜地浇水用了25﹣15＝10（分钟）；
（2）菜地离玉米地 2﹣1.1＝0.9（千米），小明从菜地到地用了37﹣25＝12（分钟）；
（3）小明给玉米地锄草用了55﹣37＝18（分钟）；
（4）玉米地离小明家2千米，小明从玉米地走回家的平均速度＝2÷＝4.8（千米/小时）．
【点评】本题考查函数图象，解答本题的关键是明确题意，利用数形结合的思想解答．
22．某游泳馆普通票价20元/张，暑假为了促销，新推出两种优惠卡：
①金卡售价600元/张，每次凭卡不再收费．
②银卡售价150元/张，每次凭卡另收10元．
暑假普通票正常出售，两种优惠卡仅限暑假使用，不限次数．设游泳x次时，所需总费用为y元
（1）分别写出选择银卡、普通票消费时，y与x之间的函数关系式；
（2）在同一坐标系中，若三种消费方式对应的函数图象如图所示，请求出点A、B、C的坐标；
（3）请根据函数图象，直接写出选择哪种消费方式更合算．

【分析】（1）根据银卡售价150元/张，每次凭卡另收10元，以及旅游馆普通票价20元/张，设游泳x次时，分别得出所需总费用为y元与x的关系式即可；
（2）利用函数交点坐标求法分别得出即可；
（3）利用（2）的点的坐标以及结合得出函数图象得出答案．
【解答】解：（1）由题意可得：银卡消费：y＝10x+150，普通消费：y＝20x；

（2）由题意可得：当10x+150＝20x，
解得：x＝15，则y＝300，
故B（15，300），
当y＝10x+150，x＝0时，y＝150，故A（0，150），
当y＝10x+150＝600，
解得：x＝45，则y＝600，
故C（45，600）；

（3）如图所示：由A，B，C的坐标可得：
当0＜x＜15时，普通消费更划算；
当x＝15时，银卡、普通票的总费用相同，均比金卡合算；
当15＜x＜45时，银卡消费更划算；
当x＝45时，金卡、银卡的总费用相同，均比普通票合算；
当x＞45时，金卡消费更划算．
【点评】此题主要考查了一次函数的应用，根据数形结合得出自变量的取值范围得出是解题关键．