2020-2021学年重庆市沙坪坝区南开中学八年级（下）期末数学模拟练习试卷（1）

这是一份2020-2021学年重庆市沙坪坝区南开中学八年级（下）期末数学模拟练习试卷（1），共35页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2020-2021学年重庆市沙坪坝区南开中学八年级（下）期末数学模拟练习试卷（1）
一、选择题:(本大题12个小题，每小题4分，共48分)
1．（4分）下列各数中，比﹣1小的数是（　　）
A．2 B．1 C．0 D．﹣2
2．（4分）下面在线学习平台的图标中，是轴对称图形的是（　　）
A． B．
C． D．
3．（4分）下列各式正确的是（　　）
A．2a2+3a2＝5a4 B．a2•a＝a3
C．（a2）3＝a5 D．＝a
4．（4分）已知x＝2是一元二次方程x2+ax+b＝0的解，则4a+2b+1的值是（　　）
A．﹣6 B．﹣8 C．﹣5 D．﹣7
5．（4分）如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF＝3，则菱形ABCD的周长是（　　）

A．12 B．16 C．20 D．24
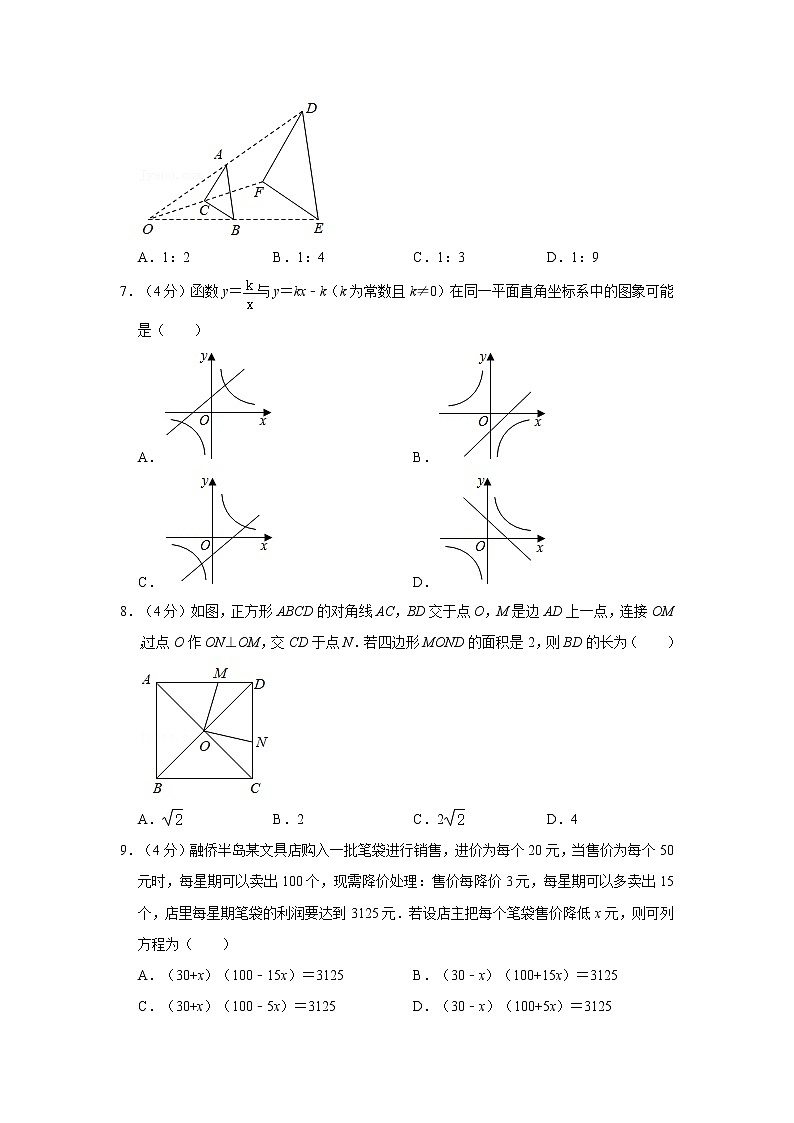
6．（4分）如图，△ABC与△DEF位似，点O是它们的位似中心，其中OE＝2OB，则△ABC与△DEF的周长之比是（　　）

A．1：2 B．1：4 C．1：3 D．1：9
7．（4分）函数y＝与y＝kx﹣k（k为常数且k≠0）在同一平面直角坐标系中的图象可能是（　　）
A． B．
C． D．
8．（4分）如图，正方形ABCD的对角线AC，BD交于点O，M是边AD上一点，连接OM，过点O作ON⊥OM，交CD于点N．若四边形MOND的面积是2，则BD的长为（　　）

A． B．2 C．2 D．4
9．（4分）融侨半岛某文具店购入一批笔袋进行销售，进价为每个20元，当售价为每个50元时，每星期可以卖出100个，现需降价处理：售价每降价3元，每星期可以多卖出15个，店里每星期笔袋的利润要达到3125元．若设店主把每个笔袋售价降低x元，则可列方程为（　　）
A．（30+x）（100﹣15x）＝3125 B．（30﹣x）（100+15x）＝3125
C．（30+x）（100﹣5x）＝3125 D．（30﹣x）（100+5x）＝3125
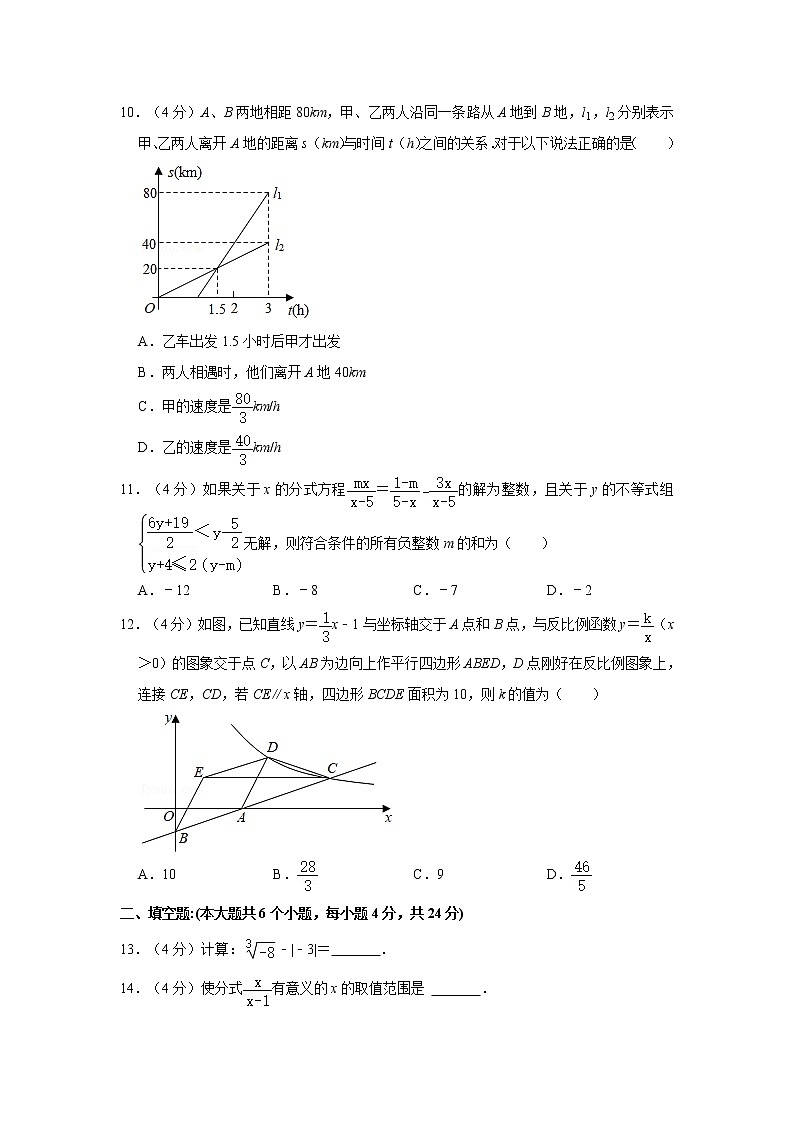
10．（4分）A、B两地相距80km，甲、乙两人沿同一条路从A地到B地，l1，l2分别表示甲、乙两人离开A地的距离s（km）与时间t（h）之间的关系．对于以下说法正确的是（　　）

A．乙车出发1.5小时后甲才出发
B．两人相遇时，他们离开A地40km
C．甲的速度是km/h
D．乙的速度是km/h
11．（4分）如果关于x的分式方程＝的解为整数，且关于y的不等式组无解，则符合条件的所有负整数m的和为（　　）
A．﹣12 B．﹣8 C．﹣7 D．﹣2
12．（4分）如图，已知直线y＝x﹣1与坐标轴交于A点和B点，与反比例函数y＝（x＞0）的图象交于点C，以AB为边向上作平行四边形ABED，D点刚好在反比例图象上，连接CE，CD，若CE∥x轴，四边形BCDE面积为10，则k的值为（　　）

A．10 B． C．9 D．
二、填空题:(本大题共6个小题，每小题4分，共24分)
13．（4分）计算：﹣|﹣3|＝　 　．
14．（4分）使分式有意义的x的取值范围是 　 　．
15．（4分）在桌面上放有四张背面完全一样的卡片，卡片的正面分别标有数字﹣2，0，3，5．把四张卡片背面朝上，随机抽取一张，记下数字且不放回，再从中随机抽取一张．则两次抽取卡片上的数字之和为负数的概率是 　 　．
16．（4分）若关于x的一元二次方程（m﹣2）x2﹣2x+1＝0有实根，则m的取值范围是　 　．
17．（4分）如图，点E在矩形ABCD边CD上，将△ADE沿AE翻折，点D恰好落在BC上的点F处，若AB＝2CF，CE＝3，连接DF，与AE交于H点，连接BH，则点F到BH的距离为 　 　．

18．（4分）“手中有粮，心中不慌”．为优选品种，提高农作物产量，某农业科技小组对A，B，C三个小麦品种进行种植对比研究．去年A，B，C三个品种各种植了相同的面积，但产量不同．收获后A，B，C三个品种的售价之比为2：3：5，全部售出后，三个品种的总销售额是其中C品种销售额的3倍．今年，科技小组加大了小麦种植的科研力度，在A，B，C种植亩数不变的情况下，预计A，B，C三个品种平均亩产量将在去年的基础上分别增加、和、由于B品种深受市场的欢迎，预计每千克售价将在去年的基础上上涨50%，A、C两个品种的售价不变．若B，C两个品种今年全部售出后销售额之比是7：6．则今年A，C两个品种的产量之比是　 　．
三、解答题:(本大题共9个小题，共78分)解答时每小题必须给出必要的演算过程或推理步骤.
19．（8分）解方程：
（1）；
（2）（x﹣2）2＝3（x﹣2）．
20．（8分）（1）化简：（2x+y）2﹣x（x+4y）；
（2）化简：a﹣1+÷．
21．（6分）如图，在▱ABCD中，AE平分∠BAD交BD于点E，交BC于点M．
（1）尺规作图：作∠BCD的平分线CN，交BD于点F．（基本作图，保留作图痕迹，不写作法，并标明字母）
（2）求证：AE＝CF．

22．（8分）为提高学生体育与健康素养，增强体质健康管理的意识和能力，各学校都在深入开展体育教育．某校为了解七、八年级学生每日体育运动的时间（单位：分钟）情况，从该校七、八年级中各随机抽查了20名学生进行问卷调查，并将调查结果进行整理，描述和分析（A：0≤t＜20，B：20≤t＜40，C：40≤t＜60，D：60≤t＜80，E：80≤t＜100），给出了部分信息：
七年级抽取的学生在C组的每日体育运动时间为：40，40，50，55．
八年级抽取的20名学生的每日体育运动时间为：10，15，20，25，30，35，40，40，45，50，50，50，55，60，60，75，75，80，90，95．
七八年级抽取的学生每日体育运动时间的统计量
年级
平均数
众数
中位数
方差
七年级
50
35
a
580
八年级
50
b
50
560
根据以上信息，解答下列问题：
（1）直接写出a＝　 　，b＝　 　，m＝　 　；
（2）根据以上数据，在该校七、八年级中，你认为哪个年级参加体育运动的情况较好？请说明理由：　 　；（写一条理由即可）
（3）若该校七、八年级共有学生1600人，试估计该校七、八年级学生每日体育运动时间不少于60分钟的人数之和．

23．（10分）探究函数性质时，我们经历了列表、描点、连线画函数图象，观察分析图象特征，概括函数性质的过程．以下是我们研究函数y＝x+|﹣2x+6|+m性质及其应用的部分过程，请按要求完成下列各小题．
x
…
﹣2
﹣1
0
1
2
3
4
5
…
y
…
6
5
4
a
2
1
b
7
…
（1）写出函数关系式中m及表格中a，b的值：
m＝　 　，a＝　 　，b＝　 　；
（2）根据表格中的数据在所给的平面直角坐标系中画出该函数的图象，并根据图象写出该函数的一条性质：　 　；
（3）已知函数y＝的图象如图所示，结合你所画的函数图象，直接写出不等式x+|﹣2x+6|+m＞的解集．

24．（10分）考虑到市民“五一”假期短途出行需求，某旅行社推出A和B两个旅行产品．“五一”前一周，接待参加A和B的游客共700人，其中选择B的人数不低于选择A人数的．
（1）“五一”前一周选择B的游客至少有多少人？
（2）已知“五一”前一周，A价格为360元/人，B价格为700元/人，且选择B的游客人数恰好是（1）中的最小值．“五一”假期期间，为了提高销量，B的售价比前一周B售价下降a%，选择B的人数比前一周的最少人数增加a%，A的售价比前一周A的售价下降a%，选择A的人数与前一周相同．结果“五一”假期期间总销售额为354000元，求a的值．
25．（10分）对任意一个三位数m，如果m满足各个数位上的数字互不相同，且都不为零，则称这个数为“特异数”，将m的百位数字调到个位可以得到一个新的三位数，不断重复此操作共可得到两个不同的新三位数，把这两个新数与原数m的和与111的商记为F（m）．例如，123是“特异数”，不断将123的百位数字调到个位可得231，312，F（123）＝＝6．
（1）求F（456），F（321）；
（2）已知s＝100x+32，t＝256+y（1≤x≤y≤9，x，y为整数），若s、t均为“特异数”，且F（s）+F（t）可被6整除，求F（s）•F（t）的最大值．
26．（10分）如图，在平面直角坐标系中，直线AB分别与x轴的负半轴、y轴的正半轴交于A、B两点，其中OA＝2，S△ABC＝12，点C在x轴的正半轴上，且OC＝OB．
（1）求直线AB的解析式；
（2）将直线AB向下平移6个单位长度得到直线l1，直线l1与y轴交于点E，与直线CB交于点D，过点E作y轴的垂线l2，若点P为y轴上一个动点，Q为直线l2上一个动点，求PD+PQ+DQ的最小值；
（3）若点M为直线AB上的一点，在y轴上是否存在点N，使以点A、D、M、N为顶点的四边形为平行四边形，若存在，请直接写出点N的坐标；若不存在，请说明理由．
27．（8分）如图，在△ABC中，AC＝BC，∠ACB＝120°，点D是AB边上一点，连接CD，以CD为边作等边△CDE．

（1）如图1，若∠CDB＝45°，AB＝6，求等边△CDE的边长；
（2）如图2，点D在AB边上移动过程中，连接BE，取BE的中点F，连接CF，DF，过点D作DG⊥AC于点G．
①求证：CF⊥DF；
②如图3，将△CFD沿CF翻折得△CFD′，连接BD′，直接写出的最小值．

2020-2021学年重庆市沙坪坝区南开中学八年级（下）期末数学模拟练习试卷（1）
参考答案与试题解析
一、选择题:(本大题12个小题，每小题4分，共48分)
1．（4分）下列各数中，比﹣1小的数是（　　）
A．2 B．1 C．0 D．﹣2
【分析】根据两个负数比较大小，绝对值大的负数反而小，可得答案．
【解答】解：∵﹣2＜﹣1＜0＜2，
∴比﹣1小的数是﹣2，
故选：D．
【点评】本题考查了有理数的大小比较，注意：正数都大于0，负数都小于0，两个负数比较大小，其绝对值大的反而小．
2．（4分）下面在线学习平台的图标中，是轴对称图形的是（　　）
A． B．
C． D．
【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴可得答案．
【解答】解：A、不是轴对称图形，故此选项不合题意；
B、不是轴对称图形，故此选项不合题意；
C、不是轴对称图形，故此选项不合题意；
D、是轴对称图形，故此选项符合题意；
故选：D．
【点评】此题主要考查了轴对称图形，关键是掌握轴对称图形的概念．
3．（4分）下列各式正确的是（　　）
A．2a2+3a2＝5a4 B．a2•a＝a3
C．（a2）3＝a5 D．＝a
【分析】分别根据合并同类项的法则、同底数幂的乘法法则、幂的乘方法则以及二次根式的性质解答即可．
【解答】解：A、2a2+3a2＝5a2，故选项A不合题意；
B、a2•a＝a3，故选项B符合题意；
C、（a2）3＝a6，故选项C不合题意；
D、＝|a|，故选项D不合题意．
故选：B．
【点评】本题主要考查了合并同类项的法则、幂的运算法则以及二次根式的性质，熟练掌握相关运算性质是解答本题的关键．
4．（4分）已知x＝2是一元二次方程x2+ax+b＝0的解，则4a+2b+1的值是（　　）
A．﹣6 B．﹣8 C．﹣5 D．﹣7
【分析】把方程的解代入方程，求得2a+b的值，然后整体代人即可．
【解答】解：∵x＝2是一元二次方程x2+ax+b＝0的解，
∴4+2a+b＝0，
∴2a+b＝﹣4，
∴4a+2b+1＝2（2a+b）+1＝2×（﹣4）+1＝﹣7，
故选：D．
【点评】本题考查的是一元二次方程的解，把方程的解代入方程可以求出代数式2a+b的值，难度不大．
5．（4分）如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF＝3，则菱形ABCD的周长是（　　）

A．12 B．16 C．20 D．24
【分析】根据三角形的中位线平行于第三边并且等于第三边的一半求出BC，再根据菱形的周长公式列式计算即可得解．
【解答】解：∵E、F分别是AB、AC的中点，
∴EF是△ABC的中位线，
∴BC＝2EF＝2×3＝6，
∴菱形ABCD的周长＝4BC＝4×6＝24．
故选：D．
【点评】本题主要考查了菱形的四条边都相等，三角形的中位线平行于第三边并且等于第三边的一半，求出菱形的边长是解题的关键．
6．（4分）如图，△ABC与△DEF位似，点O是它们的位似中心，其中OE＝2OB，则△ABC与△DEF的周长之比是（　　）

A．1：2 B．1：4 C．1：3 D．1：9
【分析】根据位似图形的概念得到BC∥EF，进而证明△OBC∽△OEF，根据相似三角形的性质解答即可．
【解答】解：∵△ABC与△DEF位似，
∴△ABC∽△DEF，BC∥EF，
∴△OBC∽△OEF，
∴＝＝，即△ABC与△DEF的相似比为1：2，
∴△ABC与△DEF的周长之比为1：2，
故选：A．
【点评】本题考查的是位似图形的概念和性质、相似三角形的性质，掌握位似图形的对应边平行是解题的关键．
7．（4分）函数y＝与y＝kx﹣k（k为常数且k≠0）在同一平面直角坐标系中的图象可能是（　　）
A． B．
C． D．
【分析】分别根据反比例函数及一次函数图象的特点对四个选项进行逐一分析即可．
【解答】解：A、∵由反比例函数的图象在一、三象限可知，k＞0，∴﹣k＜0，∴一次函数y＝kx﹣k的图象经过一、三、四象限，故本选项错误；
B、∵由反比例函数的图象在二、四象限可知，k＜0，∴﹣k＞0，∴一次函数y＝kx﹣k的图象经过一、二、四象限，故本选项错误；
C、∵由反比例函数的图象在一、三象限可知，k＞0，∴﹣k＜0，∴一次函数y＝kx﹣k的图象经过一、三、四象限，故本选项正确；
D、∵由反比例函数的图象在一、三象限可知，k＞0，∴﹣k＜0，∴一次函数y＝kx﹣k的图象经过一、三、四象限，故本选项错误；
故选：C．
【点评】本题考查的是反比例函数及一次函数图象，解答此题的关键是先根据反比例函数所在的象限判断出k的符号，再根据一次函数的性质进行解答．
8．（4分）如图，正方形ABCD的对角线AC，BD交于点O，M是边AD上一点，连接OM，过点O作ON⊥OM，交CD于点N．若四边形MOND的面积是2，则BD的长为（　　）

A． B．2 C．2 D．4
【分析】利用正方形的性质得到OD＝OB＝OC，∠COD＝90°，∠OCD＝∠ODA＝45°，利用等角的余角相等可证得∠CON＝∠DOM，则可判断△OCN≌△ODM，所以S△OCN＝S△ODM，从而得到S△ODC＝S四边形MOND＝2，然后利用等腰三角形的面积计算出OD即可．
【解答】解：∵四边形ABCD为正方形，
∴OD＝OB＝OC，∠COD＝90°，∠OCD＝∠ODA＝45°，
∵ON⊥OM，
∴∠MON＝90°，
∵∠CON+∠DON＝90°，∠DOM+∠DON＝90°，
∴∠CON＝∠DOM，
在△OCN和△ODM中，
，
∴△OCN≌△ODM（ASA），
∴S△OCN＝S△ODM，
∴S△OCN+S△DON+S△ODM+S△DON，
即S△ODC＝S四边形MOND＝2，
∵OD•OC＝2，
而OD＝OC，
∴OD＝2，
∴BD＝2OD＝4．
故选：D．
【点评】本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角；两条对角线将正方形分成四个全等的等腰直角三角形．证明△OCN≌△ODM是解决问题的关键．
9．（4分）融侨半岛某文具店购入一批笔袋进行销售，进价为每个20元，当售价为每个50元时，每星期可以卖出100个，现需降价处理：售价每降价3元，每星期可以多卖出15个，店里每星期笔袋的利润要达到3125元．若设店主把每个笔袋售价降低x元，则可列方程为（　　）
A．（30+x）（100﹣15x）＝3125 B．（30﹣x）（100+15x）＝3125
C．（30+x）（100﹣5x）＝3125 D．（30﹣x）（100+5x）＝3125
【分析】若设店主把每个笔袋售价降低x元，根据总利润达到3125元列出方程即可．
【解答】解：根据题意得：（30﹣x）（100+5x）＝3125，
故选：D．
【点评】本题考查了由实际问题抽象出一元二次方程的知识，解题的关键是能够分别表示出单价和单件的利润，从而表示出总利润．
10．（4分）A、B两地相距80km，甲、乙两人沿同一条路从A地到B地，l1，l2分别表示甲、乙两人离开A地的距离s（km）与时间t（h）之间的关系．对于以下说法正确的是（　　）

A．乙车出发1.5小时后甲才出发
B．两人相遇时，他们离开A地40km
C．甲的速度是km/h
D．乙的速度是km/h
【分析】根据题意和函数图象中的数据，可以判断各个小题中的结论是否正确，从而可以解答本题．
【解答】解：由图可得，
乙车出发1.5小时后甲已经出发一段时间，故选项A不合题意；
两人相遇时，他们离开A地20km，故选项B不合题意；
甲的速度是（80﹣20）÷（3﹣1.5）＝40（km/h），故选项C不合题意；
乙的速度是40÷3＝（km/h），故选项D符合题意．
故选：D．
【点评】本题考查一次函数的应用，解答本题的关键是明确题意，利用数形结合的思想解答．
11．（4分）如果关于x的分式方程＝的解为整数，且关于y的不等式组无解，则符合条件的所有负整数m的和为（　　）
A．﹣12 B．﹣8 C．﹣7 D．﹣2
【分析】先解分式方程，再由不等式组无解确定m的范围，最后求出满足条件的所有整数m的和即可．
【解答】解：分式方程去分母，得：mx＝m﹣1﹣3x，
解得：x＝，
由，
解不等式①，得：y＜﹣6，
解不等式②，得：y≥4+2m，
∵不等式组无解，
∴4+2m≥﹣6，
解得：m≥﹣5，
∵分式方程的解为整数，且x≠5，
∴符合条件的所有负整数m有﹣5；﹣2；﹣1；
它们的和为（﹣5）+（﹣2）+（﹣1）＝﹣8，
故选：B．
【点评】本题考查了分式方程的解以及解一元一次不等式组，根据分式方程的解为整数结合不等式组无解，找出满足条件m的值是解题的关键．
12．（4分）如图，已知直线y＝x﹣1与坐标轴交于A点和B点，与反比例函数y＝（x＞0）的图象交于点C，以AB为边向上作平行四边形ABED，D点刚好在反比例图象上，连接CE，CD，若CE∥x轴，四边形BCDE面积为10，则k的值为（　　）

A．10 B． C．9 D．
【分析】设点D坐标为（m，），通过含m，k的代数式分别表示出C，E的坐标，再通过含参代数式表示四边形BCDE面积求解．
【解答】解：由y＝x﹣1可得A（3，0），B（0，﹣1），
设点D坐标为（m，），
由平行四边形ABED可得点E坐标为（m﹣3，﹣1），
∵CE∥x轴，
∴点C纵坐标为﹣1，
将y＝﹣1代入y＝x﹣1可得x＝，
将x＝代入y＝得y＝，
∴﹣1＝，
解得k＝m2+m．
作DH⊥EC于点H，CG⊥y轴于点G，

∴S四边形BCDE＝S△CDE+S△BCE＝EC•DHEC•BG＝EC（DH+BG），
＝（﹣m+3）（﹣+1+﹣1+1），
＝（﹣m+3）（+1），
将k＝m2+m代入（﹣m+3）（+1）得m+6＝10，
∴m＝4，k＝m2+m＝，
故选：B．
【点评】本题考查反比例函数的综合应用，解题关键是通过参数表示点坐标从而求解．
二、填空题:(本大题共6个小题，每小题4分，共24分)
13．（4分）计算：﹣|﹣3|＝　﹣5　．
【分析】首先计算开方和绝对值，然后计算减法，求出算式的值是多少即可．
【解答】解：﹣|﹣3|
＝﹣2﹣3
＝﹣5．
故答案为：﹣5．
【点评】此题主要考查了实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．
14．（4分）使分式有意义的x的取值范围是 　x≠1　．
【分析】先根据分式有意义的条件列出关于x的不等式，求出x的取值范围即可．
【解答】解：∵分式有意义，
∴x﹣1≠0，解得x≠1．
故答案为：x≠1．
【点评】本题考查的是分式有意义的条件，即分式的分母不为0．
15．（4分）在桌面上放有四张背面完全一样的卡片，卡片的正面分别标有数字﹣2，0，3，5．把四张卡片背面朝上，随机抽取一张，记下数字且不放回，再从中随机抽取一张．则两次抽取卡片上的数字之和为负数的概率是 　　．
【分析】画树状图，共有12种等可能的结果，两次抽取卡片上的数字之和为负数的结果有2种，再由概率公式求解即可．
【解答】解：画树状图如图：

共有12种等可能的结果，两次抽取卡片上的数字之和为负数的结果有2种，
∴两次抽取卡片上的数字之和为负数的概率是＝，
故答案为：．
【点评】本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．用到的知识点为：概率＝所求情况数与总情况数之比．
16．（4分）若关于x的一元二次方程（m﹣2）x2﹣2x+1＝0有实根，则m的取值范围是　m≤3且m≠2　．
【分析】根据根的判别式和一元二次方程的定义得出Δ＝（﹣2）2﹣4×（m﹣2）×1≥0且m﹣2≠0，解之可得答案．
【解答】解：根据题意，得：Δ＝（﹣2）2﹣4×（m﹣2）×1≥0且m﹣2≠0，
解得m≤3且m≠2，
故答案为：m≤3且m≠2．
【点评】本题主要考查一元二次方程的定义和根的判别式，一元二次方程ax2+bx+c＝0（a≠0）的根与Δ＝b2﹣4ac有如下关系：
①当Δ＞0时，方程有两个不相等的两个实数根；
②当Δ＝0时，方程有两个相等的两个实数根；
③当Δ＜0时，方程无实数根．
17．（4分）如图，点E在矩形ABCD边CD上，将△ADE沿AE翻折，点D恰好落在BC上的点F处，若AB＝2CF，CE＝3，连接DF，与AE交于H点，连接BH，则点F到BH的距离为 　　．

【分析】在Rt△EFC和Rt△ABF中，分别利用勾股定理求得DE、AD的长，再利用三角形面积公式即可求得．
【解答】解：根据折叠的性质知：AD＝AF＝BC，DE＝EF，
AE是线段DF的垂直平分线，H是DF的中点，
设DE＝EF＝x，则DC＝AB＝x+3，FC＝AB＝（x+3），
在Rt△EFC中，
FC2+EC2＝EF2，
即[（x+3）]2+32＝x2，
解得：x＝5或x＝﹣3（舍去），
∴DC＝AB＝5+3＝8，FC＝4，
设AD＝AF＝BC＝y，则BF＝y﹣4，
在Rt△ABF中，
AB2+BF2＝AF2，
即82+（y﹣4）2＝y2，
解得：y＝10，
∴BF＝6，
过H作HN⊥BC于N，过F作FM⊥BH于M，

∵四边形ABCD是矩形，
∴∠C＝90°，
∴HN∥CD，
∴HN＝CD＝4，FN＝FC＝2，
∴BN＝BF+FN＝8，
由勾股定理得：BH＝＝4，
∵S△BHF＝BF×HN＝BH×FM，
∴FM＝＝＝，
故答案为：．
【点评】本题考查了矩形的性质、翻折变换、勾股定理等知识，关键是正确作出辅助线，利用勾股定理构建方程解决问题．
18．（4分）“手中有粮，心中不慌”．为优选品种，提高农作物产量，某农业科技小组对A，B，C三个小麦品种进行种植对比研究．去年A，B，C三个品种各种植了相同的面积，但产量不同．收获后A，B，C三个品种的售价之比为2：3：5，全部售出后，三个品种的总销售额是其中C品种销售额的3倍．今年，科技小组加大了小麦种植的科研力度，在A，B，C种植亩数不变的情况下，预计A，B，C三个品种平均亩产量将在去年的基础上分别增加、和、由于B品种深受市场的欢迎，预计每千克售价将在去年的基础上上涨50%，A、C两个品种的售价不变．若B，C两个品种今年全部售出后销售额之比是7：6．则今年A，C两个品种的产量之比是　14：5　．
【分析】用未知数表示出A，B，C三个小麦去年的产量和售价，再根据题意表示出今年的产量和售价，列方程．因为都和C有关系，可以用C的未知数表示另外两种，从而可求出．
【解答】解：设A，B，C三个小麦去年的产量分别为x、y、z，去年的售价为2a、3a、5a，则今年A，B，C三个小麦的产量为x，y，z，售价为2a、4.5a、5a．
∴＝，
∴18y＝25z，
∴y＝z．
∵三个品种的总销售额是其中C品种销售额的3倍，
∴2ax+3ay+5az＝3×5az，
∴2x+3y＝10z，
∴x＝z．
∴今年A，C两个品种的产量之比是（x）：（z）＝14：5．
故答案为14：5．
【点评】此题考查的是三元一次方程的应用，涉及到多个未知数，掌握代入消元法是解题的关键．
三、解答题:(本大题共9个小题，共78分)解答时每小题必须给出必要的演算过程或推理步骤.
19．（8分）解方程：
（1）；
（2）（x﹣2）2＝3（x﹣2）．
【分析】（1）先两边都乘以3（2x﹣1）化分式方程为整式方程，解之求出x的值，再检验即可得出答案；
（2）利用因式分解法求解即可．
【解答】解：（1）两边都乘以3（2x﹣1），得：2x﹣1﹣6＝1，
解得x＝4，
经检验x＝4是原方程的解，
所以原方程的解为x＝4．
（2））（x﹣2）2﹣3（x﹣2）＝0，
（x﹣2）（x﹣2﹣3）＝0，
∴x﹣2＝0或x﹣5＝0，
∴x1＝2，x2＝5．
【点评】本题主要考查解分式方程和一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
20．（8分）（1）化简：（2x+y）2﹣x（x+4y）；
（2）化简：a﹣1+÷．
【分析】（1）先利用完全平方公式和单项式乘多项式的法则计算乘方和乘法，然后再合并同类项；
（2）先算除法，然后再算加减．
【解答】解：（1）原式＝4x2+4xy+y2﹣x2﹣4xy
＝3x2+y2；
（2）原式＝a﹣1+
＝a﹣1+
＝a﹣1+
＝
＝
＝．
【点评】本题考查整式的混合运算，分式的混合运算，掌握运算顺序和计算法则是解题关键．
21．（6分）如图，在▱ABCD中，AE平分∠BAD交BD于点E，交BC于点M．
（1）尺规作图：作∠BCD的平分线CN，交BD于点F．（基本作图，保留作图痕迹，不写作法，并标明字母）
（2）求证：AE＝CF．

【分析】（1）利用基本作图作∠BCD的平分线；
（2）先利用平行四边形的性质得到AB＝CD，AB∥CD，∠BAC＝∠BCD，则∠ABE＝∠DCF，∠ABE＝∠CDF，然后证明△ABE≌△CDF，从而得到结论．
【解答】（1）解：如图，CN为所作；

（2）证明：∵四边形ABCD为平行四边形，
∴AB＝CD，AB∥CD，∠BAC＝∠BCD，
∵AE平分∠BAD，CN平分∠BCD，
∴∠BAE＝∠BAD，∠DCF＝∠BCD，
∴∠ABE＝∠DCF，
∵AB∥CD，
∴∠ABE＝∠CDF，
在Rt△ABE和△CDF中，
，
∴△ABE≌△CDF（ASA），
∴AE＝CF．
【点评】本题考查了作图﹣基本作图：熟练掌握5种基本作图（作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线）．也考查了全等三角形的判定与性质和平行四边形的性质．
22．（8分）为提高学生体育与健康素养，增强体质健康管理的意识和能力，各学校都在深入开展体育教育．某校为了解七、八年级学生每日体育运动的时间（单位：分钟）情况，从该校七、八年级中各随机抽查了20名学生进行问卷调查，并将调查结果进行整理，描述和分析（A：0≤t＜20，B：20≤t＜40，C：40≤t＜60，D：60≤t＜80，E：80≤t＜100），给出了部分信息：
七年级抽取的学生在C组的每日体育运动时间为：40，40，50，55．
八年级抽取的20名学生的每日体育运动时间为：10，15，20，25，30，35，40，40，45，50，50，50，55，60，60，75，75，80，90，95．
七八年级抽取的学生每日体育运动时间的统计量
年级
平均数
众数
中位数
方差
七年级
50
35
a
580
八年级
50
b
50
560
根据以上信息，解答下列问题：
（1）直接写出a＝　45　，b＝　50　，m＝　30　；
（2）根据以上数据，在该校七、八年级中，你认为哪个年级参加体育运动的情况较好？请说明理由：　八年级劳动时间的方差小，劳动时间更加稳定　；（写一条理由即可）
（3）若该校七、八年级共有学生1600人，试估计该校七、八年级学生每日体育运动时间不少于60分钟的人数之和．

【分析】（1）根据百分比之和为1求出m的值，再根据中位数和众数的定义求解可得a、b的值；
（2）答案不唯一，合理即可；
（3）用总人数乘以七、八年级学每日体育运动时间不少于60分钟的人数之和占被调查人数的比例即可．
【解答】解：（1）m%＝1﹣（10%+20%+25%+15%）＝30%，即m＝30，
∵A、B时间段的人数为20×（10%+30%）＝8（人）、C时间段人数为4人，
∴七年级中位数a＝＝45，
八年级劳动时间50出现的最多，所以众数b＝50，
故答案为：45，50，30；
（2）八年级参加体育运动的情况较好，
理由：八年级劳动时间的方差小，劳动时间更加稳定（答案不唯一），
故答案为：八年级劳动时间的方差小，劳动时间更加稳定（答案不唯一）；
（3）该校七、八年级学生每日体育运动时间不少于60分钟的人数之和为1600×＝600（人）．
【点评】本题考查中位数、众数、方差的意义和计算方法，理解各个概念的内涵和计算方法是解题的关键．
23．（10分）探究函数性质时，我们经历了列表、描点、连线画函数图象，观察分析图象特征，概括函数性质的过程．以下是我们研究函数y＝x+|﹣2x+6|+m性质及其应用的部分过程，请按要求完成下列各小题．
x
…
﹣2
﹣1
0
1
2
3
4
5
…
y
…
6
5
4
a
2
1
b
7
…
（1）写出函数关系式中m及表格中a，b的值：
m＝　﹣2　，a＝　3　，b＝　4　；
（2）根据表格中的数据在所给的平面直角坐标系中画出该函数的图象，并根据图象写出该函数的一条性质：　当x＝3时函数有最小值y＝1　；
（3）已知函数y＝的图象如图所示，结合你所画的函数图象，直接写出不等式x+|﹣2x+6|+m＞的解集．

【分析】（1）代入一对x、y的值即可求得m的值，然后代入x＝1求a值，代入x＝4求b值即可；
（2）利用描点作图法作出图象并写出一条性质即可；
（3）根据图象求出即可．
【解答】解：（1）当x＝0时，|6|+m＝4，
解得：m＝﹣2，
即函数解析式为：y＝x+|﹣2x+6|﹣2，
当x＝1时，a＝1+|﹣2+6|﹣2＝3，
当x＝4时，b＝4+|﹣2×4+6|﹣2＝4，
故答案为：﹣2，3，4；
（2）图象如右图，根据图象可知当x＝3时函数有最小值y＝1；
（3）根据当y＝x+|﹣2x+6|﹣2的函数图象在函数y＝的图象上方时，不等式x+|﹣2x+6|﹣2＞成立，
∴x＜0或x＞4．

【点评】本题主要考查一次函数和反比例函数图象性质，熟练掌握描点作图和一次函数及反比例函数图象性质是解题的关键．
24．（10分）考虑到市民“五一”假期短途出行需求，某旅行社推出A和B两个旅行产品．“五一”前一周，接待参加A和B的游客共700人，其中选择B的人数不低于选择A人数的．
（1）“五一”前一周选择B的游客至少有多少人？
（2）已知“五一”前一周，A价格为360元/人，B价格为700元/人，且选择B的游客人数恰好是（1）中的最小值．“五一”假期期间，为了提高销量，B的售价比前一周B售价下降a%，选择B的人数比前一周的最少人数增加a%，A的售价比前一周A的售价下降a%，选择A的人数与前一周相同．结果“五一”假期期间总销售额为354000元，求a的值．
【分析】（1）设“五一”前一周选择B的游客有x人，则选择A的游客有（700﹣x）人，根据选择B的人数不低于选择A人数的，即可得出关于x的一元一次不等式，解之取其中的最小值即可得出结论；
（2）根据总销售额＝销售单价×销售数量，结合“五一”假期期间总销售额为354000元，即可得出关于a的一元二次方程，解之取其正值即可得出结论．
【解答】解：（1）设“五一”前一周选择B的游客有x人，则选择A的游客有（700﹣x）人，
依题意得：x≥（700﹣x），
解得：x≥300．
答：“五一”前一周选择B的游客至少有300人．
（2）依题意得：700（1﹣a%）×300（1+a%）+360（1﹣a%）×（700﹣300）＝354000，
整理得：6a2﹣60a＝0，
解得：a1＝10，a2＝0（不合题意，舍去）．
答：a的值为10．
【点评】本题考查了一元一次不等式的应用以及一元二次方程的应用，解题的关键是：（1）根据各数量之间的关系，正确列出一元一次不等式；（2）找准等量关系，正确列出一元二次方程．
25．（10分）对任意一个三位数m，如果m满足各个数位上的数字互不相同，且都不为零，则称这个数为“特异数”，将m的百位数字调到个位可以得到一个新的三位数，不断重复此操作共可得到两个不同的新三位数，把这两个新数与原数m的和与111的商记为F（m）．例如，123是“特异数”，不断将123的百位数字调到个位可得231，312，F（123）＝＝6．
（1）求F（456），F（321）；
（2）已知s＝100x+32，t＝256+y（1≤x≤y≤9，x，y为整数），若s、t均为“特异数”，且F（s）+F（t）可被6整除，求F（s）•F（t）的最大值．
【分析】（1）利用题干中定义计算即可；
（2）利用“特异数”的意义和F（m）的公式，分类讨论计算出F（s）和F（t），依据已知和数位上数字的特征计算后，比较大小，取最大值即可．
【解答】解：（1）∵不断将456的百位数字调到个位可得564，645，
∴F（456）＝＝15；
∵不断将的百位数字调到个位可得213，132，
∴F（321）＝＝6．
（2）∵s、t均为“特异数”，s＝100x+32，t＝256+y（1≤x≤y≤9，x，y为整数），
又6+4＝10，6+6＝12，
∴x≠2，3；y≠4，6．
∵不断将100x+32的百位数字调到个位可得32×10+x，200+10x+3，
F（s）＝＝x+5．
①∵当1≤y≤3时，不断将256+y的百位数字调到个位可得500+10（6+y）+2，100（6+y）+25，
∴F（t）＝＝13+y．
∵F（s）+F（t）可被6整除，
∴x+5+13+y＝x+y+18可被6整除．
∵1≤x≤y≤9，1≤y≤3，x，y为整数，
∴x+y＝6，只能x＝y＝3．
∵x≠3，
∴此种情形不存在．
②当y＝5，7，8，9时，不断将256+y的百位数字调到个位可，600+10（y﹣4）+2，100（y﹣4）+26，
∴F（t）＝＝4+y．
∵F（s）+F（t）可被6整除，
∴x+5+4+y＝x+y+9可被6整除．
∴x+y＝9或x+y＝15．
∵1≤x≤y≤9，x，y为整数，y＝5，7，8，9，
∴或或或．
当x＝1，y＝8时，F（s）•F（t）＝6×12＝72；
当x＝4，y＝5时，F（s）•F（t）＝9×9＝81；
当x＝6，y＝9时，F（s）•F（t）＝11×13＝143；
当x＝7，y＝8时，F（s）•F（t）＝12×12＝144；
综上，F（s）•F（t）的最大值为144．
【点评】本题主要考查了因式分解的应用，本题是阅读型题目，准确理解题意并能熟练应用题干中的定义和公式是解题的关键．
26．（10分）如图，在平面直角坐标系中，直线AB分别与x轴的负半轴、y轴的正半轴交于A、B两点，其中OA＝2，S△ABC＝12，点C在x轴的正半轴上，且OC＝OB．
（1）求直线AB的解析式；
（2）将直线AB向下平移6个单位长度得到直线l1，直线l1与y轴交于点E，与直线CB交于点D，过点E作y轴的垂线l2，若点P为y轴上一个动点，Q为直线l2上一个动点，求PD+PQ+DQ的最小值；
（3）若点M为直线AB上的一点，在y轴上是否存在点N，使以点A、D、M、N为顶点的四边形为平行四边形，若存在，请直接写出点N的坐标；若不存在，请说明理由．
【分析】（1）设OB＝OC＝m，由S△ABC＝12，得m•（m+2）＝12，可得B（0，4），设直线AB解析式为y＝kx+b，有，即得直线AB解析式为y＝2x+4；
（2）将直线ABy＝2x+4向下平移6个单位，则直线l1解析式为y＝2x﹣2，可得E（0，﹣2），垂线l2的解析式为y＝﹣2，由B（0，4），C（4，0），得直线BC解析式为y＝﹣x+4，从而可求得D（2，2），作D关于y轴的对称点D'，作D关于直线y＝﹣2对称点D''，连接D'D''交y轴于P，交直线y＝﹣2于Q，此时PD+PQ+DQ的最小，根据D'（﹣2，2），D''（2，﹣6），得直线D'D'解析式为y＝﹣2x﹣2，从而P（0，﹣2），Q（0，﹣2），故此时PD＝2，PQ＝0，DQ＝2，PD+PQ+DQ的最小值为4．
（3）设P（p，2p+4），N（0，q），而A（﹣2，0），D（2，2），①以AD、MN为对角线，此时AD中点即为MN中点，得，解得N（0，﹣2）；②以AM、DN为对角线，同理可得N（0，10）；③以AN、DM为对角线，同理可得N（0，﹣2）．
【解答】解：（1）设OB＝OC＝m，
∵OA＝2，
∴AC＝m+2，A（﹣2，0），
∵S△ABC＝12，
∴AC•OB＝12，即m•（m+2）＝12，
解得m＝4或m＝﹣6（舍去），
∴OB＝OC＝4，
∴B（0，4），
设直线AB解析式为y＝kx+b，
∴，
解得，
∴直线AB解析式为y＝2x+4；
（2）将直线ABy＝2x+4向下平移6个单位，则直线l1解析式为y＝2x﹣2，
令x＝0得y＝﹣2，
∴E（0，﹣2），垂线l2的解析式为y＝﹣2，
∵B（0，4），C（4，0），
∴直线BC解析式为y＝﹣x+4，
由得：，
∴D（2，2），
作D关于y轴的对称点D'，作D关于直线y＝﹣2对称点D''，连接D'D''交y轴于P，交直线y＝﹣2于Q，此时PD+PQ+DQ的最小，如图：

∴D'（﹣2，2），D''（2，﹣6），
设直线D'D''解析式为y＝sx+t，
则，解得，
∴直线D'D'解析式为y＝﹣2x﹣2，
令x＝0得y＝﹣2，即P（0，﹣2），
令y＝﹣2得x＝0，即Q（0，﹣2），
∴此时PD＝2，PQ＝0，DQ＝2，
∴PD+PQ+DQ的最小值为4．
（3）存在，理由如下：
设P（p，2p+4），N（0，q），而A（﹣2，0），D（2，2），
①以AD、MN为对角线，如图：

此时AD中点即为MN中点，
∴，解得，
∴N（0，﹣2）；
②以AM、DN为对角线，如图：

同理可得：，解得，
∴N（0，10）；
③以AN、DM为对角线，如图：

同理可得，解得，
∴N（0，﹣2），
综上所述，以点A、D、M、N为顶点的四边形为平行四边形，N的坐标为（0，﹣2）或（0，10）．
【点评】本题考查一次函数及应用，涉及待定系数法、一次函数图象上点坐标特征、线段和的最小值、平行四边形等知识，解题的关键是应用平行四边形对角线互相平分，列方程组解决问题．
27．（8分）如图，在△ABC中，AC＝BC，∠ACB＝120°，点D是AB边上一点，连接CD，以CD为边作等边△CDE．

（1）如图1，若∠CDB＝45°，AB＝6，求等边△CDE的边长；
（2）如图2，点D在AB边上移动过程中，连接BE，取BE的中点F，连接CF，DF，过点D作DG⊥AC于点G．
①求证：CF⊥DF；
②如图3，将△CFD沿CF翻折得△CFD′，连接BD′，直接写出的最小值．
【分析】（1）过点C作CH⊥AB于点 H，由等腰三角形的性质和直角三角形的性质可得∠A＝∠B＝30°，AH＝BH＝3，CH＝＝，由∠CDB＝45°，可得CD＝CH＝；
（2）①延长BC到N，使CN＝BC，由“SAS”可证△CEN≌△CDA，可得EN＝AD，∠N＝∠A＝30°，由三角形中位线定理可得CF∥EN，CF＝EN，可得∠BCF＝∠N＝30°，可证DG＝CF，DG∥CF，即可证四边形CFDG是矩形，可得结论；
②由“SAS”可证△EFD≌∠BFD'，可得BD'＝DE，则当CD取最小值时，有最小值，即可求解．
【解答】解：（1）如图1，过点C作CH⊥AB于点H，

∵AC＝BC，∠ACB＝120°，CH⊥AB，
∴∠A＝∠B＝30°，AH＝BH＝3，
∴CH＝＝，
∵∠CDH＝45°，CH⊥AB，
∴∠CDH＝∠DCH＝45°，
∴DH＝CH＝，CD＝CH＝，
即△CDE的边长为；
（2）①如图2，延长BC到N，使CN＝BC，

∵AC＝BC，∠ACB＝120°，
∴∠A＝∠ABC＝30°，∠NCA＝60°，
∵△ECD是等边三角形，
∴EC＝CD，∠ECD＝60°，
∴∠NCA＝∠ECD，
∴∠NCE＝∠DCA，
又∵CE＝CD，AC＝BC＝CN，
∴△CEN≌△CDA（SAS），
∴EN＝AD，∠N＝∠A＝30°，
∵BC＝CN，BF＝EF，
∴CF∥EN，CF＝EN，
∴∠BCF＝∠N＝30°，
∴∠ACF＝∠ACB﹣∠BCF＝90°，
又∵DG⊥AC，
∴CF∥DG，
∵∠A＝30°，DG⊥AC，
∴DG＝AD，
∴DG＝CF，
∴四边形CFDG是平行四边形，
又∵∠ACF＝90°，
∴四边形CFDG是矩形，
∴∠CFD＝90°
∴CF⊥DF；
②∵将△CFD沿CF翻折得△CFD′，
∴CD＝CD'，DF＝D'F，∠CFD＝∠CFD'＝90°，
由（1）知，CF⊥DF，
∴∠CFD＝90°，
由折叠知，∠CFD'＝∠CFD＝90°，
∴点D，F，D'在同一条直线上，
∴∠EFD＝∠BFD'，
又∵EF＝BF，
∴△EFD≌∠BFD'（SAS），
∴BD'＝DE，
∴BD'＝CD，
∵当BD'取最小值时，有最小值，
∴当CD取最小值时，有最小值，
∵当CD⊥AB时，CD有最小值，
∴AD＝CD，AB＝2AD＝2CD，
∴最小值＝．
【点评】本题是几何变换综合题，考查了全等三角形的判定和性质，矩形的判定和性质，等腰三角形的性质等知识，添加恰当辅助线构造全等三角形是本题的关键．