

江苏省2022中考数学冲刺复习-20解答题基础必刷60题②
展开20解答题基础必刷60题②
一十三.动点问题的函数图象(共1小题)
21.(2021•寻乌县模拟)数学活动课上,老师提出问题:如图1,有一张长,宽的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大(已知长方体的体积长宽高).
下面是探究过程,请补充完整:
(1)设小正方形的边长为,体积为,和的关系式是 ;自变量的取值范围是 ;
(2)①列表:根据(1)中所求函数关系式计算并补全表格:
1
1.3
2.2
2.7
3
2.8
2.5
1.5
0.9
②描点:根据表中的数值,继续描出2中剩余两个点;
③在平面直角坐标系中用平滑的曲线画出该函数的图象.
(3)结合画出的函数图象,解决问题:当图1中小正方形的边长约为 时,盒子的体积最大,最大值约为 (结果精确到.
一十四.一次函数的应用(共3小题)
22.(2021•惠山区校级三模)现有一辆装满防疫物资的大货车从地沿一直线公路以60千米小时的速度匀速驶向地,地志愿者协会在得到消息后决定派出志愿者车队前去接收大货车物资,志愿者的私家车车队出发时比大货车晚1个小时,车队匀速行驶途中接到志愿者协会中心电话,由原接收大货车物资改为接收从地发出的另一批滞后物资,大货车物资按原计划送达地.志愿者车队在遇到滞后物质后,立刻停车装卸搬运共花费1个小时,然后掉头按原速原路返回地(掉头时间忽略不计),并与大货车同时到达地.已知大货车和志愿者车队与地之间的距离(千米)与志愿者车队所用时间(小时)的关系如图所示,请结合图象回答下列问题:
(1)、两地之间相距 千米;志愿者车队的速度是 千米小时;
(2)求志愿者车队遇大货车并鸣笛致敬时,大货车离出发地有多远;
(3)当大货车与志愿者车队相距30千米时,大货车出发多长时间?
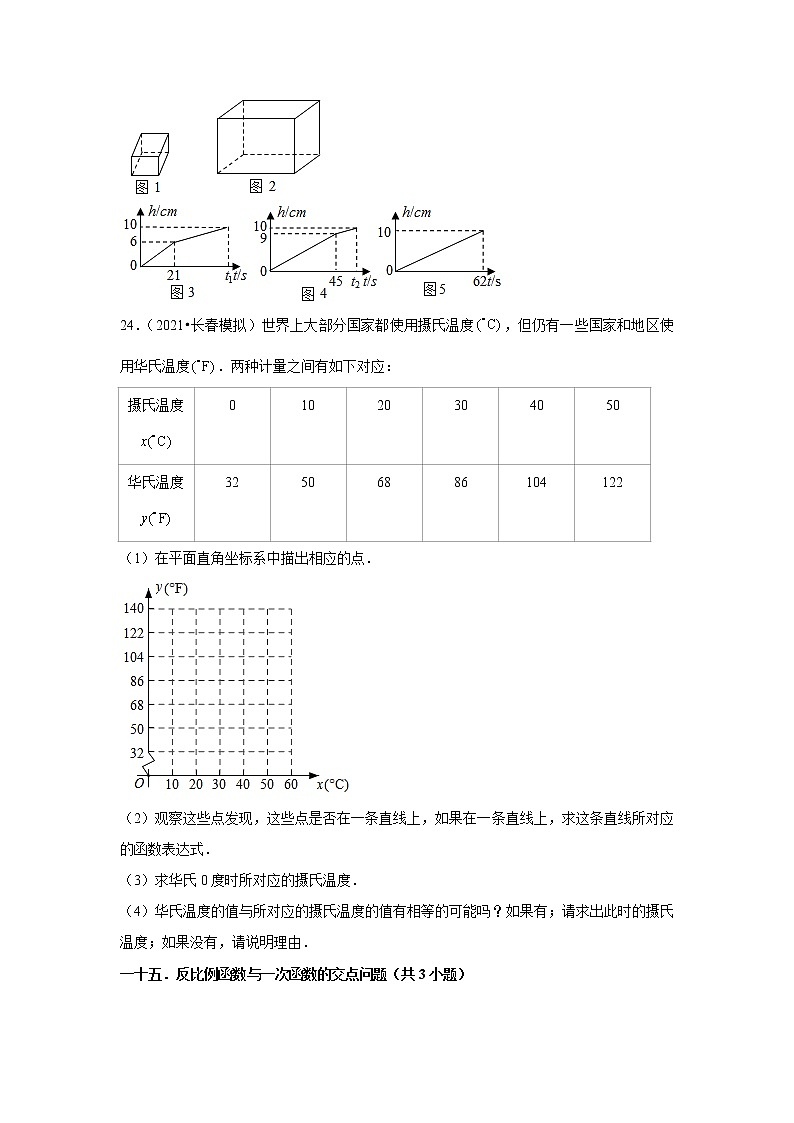
23.(2021•诸暨市模拟)将一块的长方体铁块(图平放在一个长方体水槽底部(图,现向水槽内匀速注水,直至注满水槽为止,因铁块在水槽内有3种不同的放置方式,所以水槽内的水深与注水时间的函数关系用图象来反映,其全过程有三种不同的图象(图3,图4,图(注:长度单位:厘米;时间单位:秒)
(1)判断与的大小关系: ;
(2)水槽深度为 厘米; 厘米, 厘米;
(3)求铁块的体积.
24.(2021•长春模拟)世界上大部分国家都使用摄氏温度,但仍有一些国家和地区使用华氏温度.两种计量之间有如下对应:
摄氏温度
0
10
20
30
40
50
华氏温度
32
50
68
86
104
122
(1)在平面直角坐标系中描出相应的点.
(2)观察这些点发现,这些点是否在一条直线上,如果在一条直线上,求这条直线所对应的函数表达式.
(3)求华氏0度时所对应的摄氏温度.
(4)华氏温度的值与所对应的摄氏温度的值有相等的可能吗?如果有;请求出此时的摄氏温度;如果没有,请说明理由.
一十五.反比例函数与一次函数的交点问题(共3小题)
25.(2022•南通模拟)如图,在平面直角坐标系中,直线与双曲线交于,两点,已知点的横坐标为2.
(1)求的值;
(2)求的面积;
(3)直接写出关于的不等式的解集.
26.(2022•增城区一模)已知.
(1)化简;
(2)若点是直线与反比例函数的图象的交点,求的值.
27.(2022•吉林模拟)如图,直线与双曲线相交于,两点,点在第一象限,过点作轴,垂足为点,若,的面积是1,解答下列问题:
(1)求,的值;
(2)求直线的解析式.
一十六.抛物线与x轴的交点(共1小题)
28.(2021•城阳区一模)计算:
(1)解不等式组;
(2)二次函数与轴有交点,求的取值范围.
一十七.二次函数的应用(共4小题)
29.(2022•淮阴区模拟)行驶中的汽车,在刹车后由于惯性的作用,还要继续向前滑行一段距离才停止,这段距离称为“刹车距离”,为了测定某种型号汽车的刹车性能(车速不超过,对这种汽车进行测试,测得数据如下表:
刹车时车速
0
10
20
30
40
50
60
刹车距离
0
1.1
2.4
3.9
5.6
7.5
9.6
(1)以车速为轴,以刹车距离为轴,在坐标系中描出这些数据所表示的点,并用平滑的曲线连接这些点,得到函数的大致图象;
(2)观察图象,估计函数的类型,并确定一个满足这些数据的函数解析式;
(3)该型号汽车在国道上发生了一次交通事故,现场测得刹车距离为,请推测刹车时的速度是多少?请问在事故发生时,汽车是超速行驶还是正常行驶?
30.(2021秋•鹿城区校级期中)某餐饮店每天限量供应某一爆款菜品大份袋,小份袋合计100份,且当天全部销售完毕,其成本和售价如下表所示.
份量
小份装
大份装
成本(元份)
40
60
售价(元份)
60
100
从该店店长处获悉:该餐饮店平均每天实出的小份装比大份装多40份.
(1)求该店每天销售这款爆品菜品获得的总利润.
(2)店长为了增加利润,准备提高小份装的售价,同时降低大份装的售价,售卖时发现:小份装售价每升1元,每天会少销售4份;大份装售价每降1元,每天可多销售2份.设小份装的售价提高了元为整数).每售出一份小份装可获利 元,此时大份装每天可售出 份.
(3)当取何值时,每天获利最多?最大利润为多少元?
31.(2022•东营模拟)某店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件,市场调查反映:调整价格时,售价每涨1元每月要少卖10件,售价每下降1元每月要多卖20件,为了获得更大的利润,现将商品售价调整为(元件)即售价上涨,即售价下降),每月商品销量为(件,月利润为(元.
(1)直接写出与之间的函数关系式;
(2)当销售价格是多少时才能使月利润最大?求最大月利润?
(3)为了使每月利润不少于6000元应如何控制销售价格?
32.(2022•武安市一模)如图(1),足球场上守门员李伟在处抛出一高球,球从离地面处的点飞出,其飞行的最大高度是,最高处距离飞出点的水平距离是,且飞行的路线是抛物线一部分.以点为坐标原点,竖直向上的方向为轴的正方向,球飞行的水平方向为轴的正方向建立坐标系,并把球看成一个点.(参考数据:,
(1)求足球的飞行高度与飞行水平距离之间的函数关系式;
(2)在没有队员干扰的情况下,球飞行的最远水平距离是多少?
(3)若对方一名的队员在距落点的点处,跃起进行拦截,则这名队员能拦到球吗?
(4)如图(2),在(2)的情况下,若球落地后又一次弹起,据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半,那么足球弹起后,会弹出多远?
一十八.二次函数综合题(共3小题)
33.(2022•红河州一模)如图,在平面直角坐标系中,已知抛物线与轴相交于、两点,与轴交于点.
(1)求、两点的坐标;
(2)点为直线上方抛物线上的任意一点,过点作轴交直线于点,求线段的最大值及此时点坐标;
(3)将该抛物线向右平移个单位得到新抛物线,是新抛物线对称轴上一点,在平面直角坐标系中是否存在点,使以点、、、为顶点的四边形为菱形,若存在,请直接写出点的坐标;若不存在,请说明理由.
34.(2022•锡山区校级一模)如图,在平面直角坐标系中,抛物线与轴交于点,与轴交于、两点,直线恰好经过、两点.
(1)求二次函数的表达式;
(2)点是抛物线上一动点,连接、.若的面积为6,求点的坐标;
(3)设是抛物线上的一个动点,连结,若,求点的坐标.
35.(2022•昆明模拟)如图所示,已知抛物线的对称轴为,且经过点,,与轴交于另一点.
(1)求抛物线的解析式;
(2)如图所示,若点是直线上方抛物线上的一动点,连接,,设所得的面积为,请结合图象求的取值范围;
(3)在(2)的条件下,将抛物线向右平移4个单位长度得到新抛物线,点是轴上方抛物线上一点,当的面积最大时,在轴是否存在一点,使得以点,,,为顶点的四边形是平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
一十九.全等三角形的判定与性质(共1小题)
36.(2013•北京)已知:如图,是上一点,,,.求证:.
二十.正方形的性质(共1小题)
37.(2022•渭滨区一模)如图,在正方形中,点为上一点,连接,过点作于点,并延长交于点,过点作,交于点.
求证:.
二十一.圆周角定理(共1小题)
38.(2022•泗阳县一模)如图,在中,,,求的度数.
二十二.三角形的外接圆与外心(共1小题)
39.(2022•鼓楼区一模)如图,四边形是平行四边形,,经过点,,的圆与相交于点,连接.
(1)求证:是等边三角形.
(2)是上一点,且,连接.求证:.
二十三.切线的判定与性质(共1小题)
40.(2022•泗阳县一模)如图,是的直径,射线交于点,是劣弧上一点,且,过点作于点,延长和的延长线交与点.
(1)证明:是的切线;
(2)若,,求的面积.
【参考答案】
一十三.动点问题的函数图象(共1小题)
21.(2021•寻乌县模拟)数学活动课上,老师提出问题:如图1,有一张长,宽的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大(已知长方体的体积长宽高).
下面是探究过程,请补充完整:
(1)设小正方形的边长为,体积为,和的关系式是 ;自变量的取值范围是 ;
(2)①列表:根据(1)中所求函数关系式计算并补全表格:
1
1.3
2.2
2.7
3
2.8
2.5
1.5
0.9
②描点:根据表中的数值,继续描出2中剩余两个点;
③在平面直角坐标系中用平滑的曲线画出该函数的图象.
(3)结合画出的函数图象,解决问题:当图1中小正方形的边长约为 时,盒子的体积最大,最大值约为 (结果精确到.
【解析】解:(1)根据题意得,,
化简得,;
满足,
自变量取值范围:,
故答案为:;;
(2)①当时,,
当时,,
故答案为:3,2;
②描点;
③图象见右图;
(3)结合画出的函数图象,看最高点,
当图1中小正方形的边长约为时,盒子的体积最大,最大值约为,
故答案为:0.56,3.03.
一十四.一次函数的应用(共3小题)
22.(2021•惠山区校级三模)现有一辆装满防疫物资的大货车从地沿一直线公路以60千米小时的速度匀速驶向地,地志愿者协会在得到消息后决定派出志愿者车队前去接收大货车物资,志愿者的私家车车队出发时比大货车晚1个小时,车队匀速行驶途中接到志愿者协会中心电话,由原接收大货车物资改为接收从地发出的另一批滞后物资,大货车物资按原计划送达地.志愿者车队在遇到滞后物质后,立刻停车装卸搬运共花费1个小时,然后掉头按原速原路返回地(掉头时间忽略不计),并与大货车同时到达地.已知大货车和志愿者车队与地之间的距离(千米)与志愿者车队所用时间(小时)的关系如图所示,请结合图象回答下列问题:
(1)、两地之间相距 480 千米;志愿者车队的速度是 千米小时;
(2)求志愿者车队遇大货车并鸣笛致敬时,大货车离出发地有多远;
(3)当大货车与志愿者车队相距30千米时,大货车出发多长时间?
【解析】解:(1)、两地之间相距为大货车行车路程,
大货车提前1小时出发,
大货车行车路程为,
大货车行车时间为,
志愿者行车时间为,
志愿者速度为,
故答案为:480,90;
(2)设大货车的函数表达式为,
函数图象与轴的交点为,与轴的交点为,
代入函数表达式得:,
解得:,,
大货车的函数表达式为,
设志愿者车队在内行驶路线的函数表达式为,
由题意得,,
当两车相遇时,即,
解得,
则大货车离开的时间为,
所以大货车离出发地的距离为;
(3)①横坐标在内时,
列方程得,
解得,
②在横坐标内时,
列方程得,
解得,
③在横坐标内
此时志愿者车队行驶路程的函数表达式可设为,
由函数图象得,
解得:,
解得函数的表达式为,
所以列方程的,
解得,
综上,大货车与志愿者车队相距30千米时,大货车出发多长时间或或.
23.(2021•诸暨市模拟)将一块的长方体铁块(图平放在一个长方体水槽底部(图,现向水槽内匀速注水,直至注满水槽为止,因铁块在水槽内有3种不同的放置方式,所以水槽内的水深与注水时间的函数关系用图象来反映,其全过程有三种不同的图象(图3,图4,图(注:长度单位:厘米;时间单位:秒)
(1)判断与的大小关系: ;
(2)水槽深度为 厘米; 厘米, 厘米;
(3)求铁块的体积.
【解析】解:(1)前两种是完全浸没的,注水容积相同,
所以,
故答案为:;
(2)由图3,图4可知水槽深度是;由图3知,由图4可知,
故答案为:10;6;9;
(3)根据图5注入水的体积得:,
解得:,
所以铁块的体积为.
24.(2021•长春模拟)世界上大部分国家都使用摄氏温度,但仍有一些国家和地区使用华氏温度.两种计量之间有如下对应:
摄氏温度
0
10
20
30
40
50
华氏温度
32
50
68
86
104
122
(1)在平面直角坐标系中描出相应的点.
(2)观察这些点发现,这些点是否在一条直线上,如果在一条直线上,求这条直线所对应的函数表达式.
(3)求华氏0度时所对应的摄氏温度.
(4)华氏温度的值与所对应的摄氏温度的值有相等的可能吗?如果有;请求出此时的摄氏温度;如果没有,请说明理由.
【解析】解:(1)如图,
(2)这些点在一条直线上.
设这条直线所对应的的函数表达式为.
将、代入,
得,解得,
这条直线所对应的函数表达式为:;
(3)令,得.解得,
华氏0度时所对应的摄氏温度为;
(4)有相等的可能,
令.解得,
所以华氏温度的值与所对应的摄氏温度的值相等时,摄氏温度为.
一十五.反比例函数与一次函数的交点问题(共3小题)
25.(2022•南通模拟)如图,在平面直角坐标系中,直线与双曲线交于,两点,已知点的横坐标为2.
(1)求的值;
(2)求的面积;
(3)直接写出关于的不等式的解集.
【解析】解:(1)在中,令,得,
,
,
;
(2)设直线交轴于,如图:
由得或,
,
在中令得,
,
;
(3)由图象可知:不等式的解集是或.
26.(2022•增城区一模)已知.
(1)化简;
(2)若点是直线与反比例函数的图象的交点,求的值.
【解析】解:(1)
.
(2)点是直线与反比例函数的图象的交点,
将点分别代入得,,
,
.
27.(2022•吉林模拟)如图,直线与双曲线相交于,两点,点在第一象限,过点作轴,垂足为点,若,的面积是1,解答下列问题:
(1)求,的值;
(2)求直线的解析式.
【解析】解:(1),两点是直线与双曲线的交点,
,两点关于原点对称,
,的面积是1,轴,
,
,
坐标为,坐标为
把代入和线,
得,;
(2),两点是直线与双曲线的交点,坐标为,
坐标为,
设直线解析式为,
则
解得
直线解析式为.
一十六.抛物线与x轴的交点(共1小题)
28.(2021•城阳区一模)计算:
(1)解不等式组;
(2)二次函数与轴有交点,求的取值范围.
【解析】(1)解:,
解不等式①得:,
解不等式②得,
所以不等式组无解;
(2)解:二次函数与轴有交点,
,,
且,
答:且时,二次函数与轴有交点.
一十七.二次函数的应用(共4小题)
29.(2022•淮阴区模拟)行驶中的汽车,在刹车后由于惯性的作用,还要继续向前滑行一段距离才停止,这段距离称为“刹车距离”,为了测定某种型号汽车的刹车性能(车速不超过,对这种汽车进行测试,测得数据如下表:
刹车时车速
0
10
20
30
40
50
60
刹车距离
0
1.1
2.4
3.9
5.6
7.5
9.6
(1)以车速为轴,以刹车距离为轴,在坐标系中描出这些数据所表示的点,并用平滑的曲线连接这些点,得到函数的大致图象;
(2)观察图象,估计函数的类型,并确定一个满足这些数据的函数解析式;
(3)该型号汽车在国道上发生了一次交通事故,现场测得刹车距离为,请推测刹车时的速度是多少?请问在事故发生时,汽车是超速行驶还是正常行驶?
【解析】解:(1)描点、连线为:
(2)设抛物线的解析式为,由题意,得
,
解得:.
故函数的解析式为:;
(3)当时,
;
解得:(舍去),.
,
推测刹车时的速度是,汽车是正常行驶.
30.(2021秋•鹿城区校级期中)某餐饮店每天限量供应某一爆款菜品大份袋,小份袋合计100份,且当天全部销售完毕,其成本和售价如下表所示.
份量
小份装
大份装
成本(元份)
40
60
售价(元份)
60
100
从该店店长处获悉:该餐饮店平均每天实出的小份装比大份装多40份.
(1)求该店每天销售这款爆品菜品获得的总利润.
(2)店长为了增加利润,准备提高小份装的售价,同时降低大份装的售价,售卖时发现:小份装售价每升1元,每天会少销售4份;大份装售价每降1元,每天可多销售2份.设小份装的售价提高了元为整数).每售出一份小份装可获利 元,此时大份装每天可售出 份.
(3)当取何值时,每天获利最多?最大利润为多少元?
【解析】解:(1)设该店每天大份菜品卖份,小份菜品卖份,
由题意得:,
解得:,
则,
该店总利润为(元,
该店每天销售这款爆品菜品获得的总利润为2600元;
(2)①小份菜售价提高元之后,售价为元,
利润为元
小份菜售价增加元后,销量减少了份,
则目前每天销售小份菜份,
因为该菜品每天限量100份,小份菜减少了份,则大份菜会增加份,
则大份菜销量为份.
每售出一份小份菜可获利元,大份菜可售出份,
故答案为:,;
(3)由(2)可知,大份装多售出份,
大份装降价元,
假设利润为,则
,
该二次函数开口向下,对称轴为,
是整数,
当时,有最大值,最大值为(元,
当元时,每天获利最多,最大利润为2768元.
31.(2022•东营模拟)某店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件,市场调查反映:调整价格时,售价每涨1元每月要少卖10件,售价每下降1元每月要多卖20件,为了获得更大的利润,现将商品售价调整为(元件)即售价上涨,即售价下降),每月商品销量为(件,月利润为(元.
(1)直接写出与之间的函数关系式;
(2)当销售价格是多少时才能使月利润最大?求最大月利润?
(3)为了使每月利润不少于6000元应如何控制销售价格?
【解析】解:(1)由题意可得:;
(2)由题意可得:,
化简得:,
即,
当时,,
当时,,
故当销售价格为65元时,利润最大,最大利润为6250元;
(3)由题意,如图,
令,
将代入时对应的抛物线方程,即,
解得:,
将代入时对应的抛物线方程,即,
解得,,
综上可得,,
故将销售价格控制在55元到70元之间(含55元和70元)才能使每月利润不少于6000元.
32.(2022•武安市一模)如图(1),足球场上守门员李伟在处抛出一高球,球从离地面处的点飞出,其飞行的最大高度是,最高处距离飞出点的水平距离是,且飞行的路线是抛物线一部分.以点为坐标原点,竖直向上的方向为轴的正方向,球飞行的水平方向为轴的正方向建立坐标系,并把球看成一个点.(参考数据:,
(1)求足球的飞行高度与飞行水平距离之间的函数关系式;
(2)在没有队员干扰的情况下,球飞行的最远水平距离是多少?
(3)若对方一名的队员在距落点的点处,跃起进行拦截,则这名队员能拦到球吗?
(4)如图(2),在(2)的情况下,若球落地后又一次弹起,据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半,那么足球弹起后,会弹出多远?
【解析】解:(1)①当时,,又
,
,
;
(2)令,则,解得:,(舍去)
球飞行的最远水平距离是13米;
(3)当时,,
这名队员不能拦到球;
(4)如图,足球第二次弹出后的距离为,
根据题意知(即相当于将抛物线向下平移了2个单位),
,
解得:,,
,
答:足球弹起后,会弹出10米.
一十八.二次函数综合题(共3小题)
33.(2022•红河州一模)如图,在平面直角坐标系中,已知抛物线与轴相交于、两点,与轴交于点.
(1)求、两点的坐标;
(2)点为直线上方抛物线上的任意一点,过点作轴交直线于点,求线段的最大值及此时点坐标;
(3)将该抛物线向右平移个单位得到新抛物线,是新抛物线对称轴上一点,在平面直角坐标系中是否存在点,使以点、、、为顶点的四边形为菱形,若存在,请直接写出点的坐标;若不存在,请说明理由.
【解析】解:(1)令,则,
解得或,
,,
令,则,
;
(2)设直线的解析式为,
,
,
,
设,则,
,
点为直线上方抛物线上一点,
,
当时,有最大值2,
此时;
(3)存在点,使以点、、为顶点的四边形为菱形,理由如下:
,
平移后的抛物线为,
抛物线的对称轴为直线,
设,,
①当为菱形对角线时,,
,
解得,
,,此时、重合;
②当为菱形对角线时,,
,
解得或,
或;
③当为菱形对角线时,,
,
解得或,
或;
综上所述:点坐标为或或或.
34.(2022•锡山区校级一模)如图,在平面直角坐标系中,抛物线与轴交于点,与轴交于、两点,直线恰好经过、两点.
(1)求二次函数的表达式;
(2)点是抛物线上一动点,连接、.若的面积为6,求点的坐标;
(3)设是抛物线上的一个动点,连结,若,求点的坐标.
【解析】解:(1)令,则,
,
令,则,
,
将点,代入,
,
,
;
(2)过点作轴交于点,
设,则,
,
的面积为6,
,
或,
或;
(3)设,
过点作交于点,在上截取,
,,
,,
,
时,或,
,
,
在中,,
,
,
,
在中,,
,
解得,
,
,
,
,
,
解得(舍或或,
点坐标为,或,.
35.(2022•昆明模拟)如图所示,已知抛物线的对称轴为,且经过点,,与轴交于另一点.
(1)求抛物线的解析式;
(2)如图所示,若点是直线上方抛物线上的一动点,连接,,设所得的面积为,请结合图象求的取值范围;
(3)在(2)的条件下,将抛物线向右平移4个单位长度得到新抛物线,点是轴上方抛物线上一点,当的面积最大时,在轴是否存在一点,使得以点,,,为顶点的四边形是平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.
【解析】解:(1)的对称轴为,,
抛物线经过三点,,
,
解得,
即,,,
抛物线的表达式为;
(2)设直线的解析式为,该直线过点,,
则,
解得,
故直线为的表达式为:;
过点作轴交于点,
设点的坐标为,则点,
则,
,
故面积存在最大值,
当时,面积最大值为,
;
(3)存在,或或,;
将原抛物线向右平移4个单位长度得到新抛物线,
则新抛物线的表达式为,
设点的坐标为,点,
而点、的坐标分别为、,;
①当、是对角线时,如图:
的中点即是的中点,
而的中点为,,即,,的中点为,,
,
解得或,
点的坐标为或;
②当、为对角线时,如图:
此时点都在轴下方,故舍去;
③当、为对角线时,如图:
此时,点的纵坐标与点相同,且,
即,或,,
此时的,,
综上,点的坐标为或或,.
一十九.全等三角形的判定与性质(共1小题)
36.(2013•北京)已知:如图,是上一点,,,.求证:.
【解析】证明:,
,
在和中,
,
,
.
二十.正方形的性质(共1小题)
37.(2022•渭滨区一模)如图,在正方形中,点为上一点,连接,过点作于点,并延长交于点,过点作,交于点.
求证:.
【解析】证明:四边形是正方形,
,,
,
,,
,
,
,
在和中,
,
,
.
二十一.圆周角定理(共1小题)
38.(2022•泗阳县一模)如图,在中,,,求的度数.
【解析】解:,
,
,
,
.
二十二.三角形的外接圆与外心(共1小题)
39.(2022•鼓楼区一模)如图,四边形是平行四边形,,经过点,,的圆与相交于点,连接.
(1)求证:是等边三角形.
(2)是上一点,且,连接.求证:.
【解析】证明:(1)四边形是平行四边形,,
,
四边形是圆内接四边形,
,
,
,
,
,
是等边三角形;
(2)是等边三角形,
,
,,
是等边三角形,
,
,
,
,
,
.
二十三.切线的判定与性质(共1小题)
40.(2022•泗阳县一模)如图,是的直径,射线交于点,是劣弧上一点,且,过点作于点,延长和的延长线交与点.
(1)证明:是的切线;
(2)若,,求的面积.
【解析】解:(1)如图,连接,
,
,
,
,
,
,
,
是的切线;
(2)设,
在中,,,
由可得,
解得:,
即,
则.
安徽省九年级2022中考数学冲刺复习-20解答题基础必刷60题②: 这是一份安徽省九年级2022中考数学冲刺复习-20解答题基础必刷60题②,共28页。试卷主要包含了两点,与x轴交于点C,的性质时,,且对称轴为直线x=1等内容,欢迎下载使用。
江苏省2022中考数学冲刺复习-02选择题基础必刷60题②: 这是一份江苏省2022中考数学冲刺复习-02选择题基础必刷60题②,共12页。试卷主要包含了方程的解是,已知函数,则自变量的取值范围是,函数中, 自变量的取值范围是,函数的自变量的取值范围是,函数中自变量的取值范围是,下列函数中是二次函数的是,抛物线与轴交点的个数是等内容,欢迎下载使用。
江苏省2022中考数学冲刺复习-22解答题提升必刷60题①: 这是一份江苏省2022中考数学冲刺复习-22解答题提升必刷60题①,共21页。试卷主要包含了计算,0+2﹣1;,计算或化简,,其中a=+1,分解因式,解方程等内容,欢迎下载使用。












