2022年山东省济南市初中学业水平考试数学模拟卷一

这是一份2022年山东省济南市初中学业水平考试数学模拟卷一，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

注意事项：
本试卷共三大题，共27小题，满分120分，考试时间为150分钟
全卷包括“试题卷”和“答题卡”两部分
请将答案正确填写在答题卡上，在“试题卷”上答题无效
考试结束后，请将“试题卷”和“答题卡”一并交回
一、选择题（每小题4分，有12小题，共48分）
1．下列说法中，错误的是（ ）.
A．4的算术平方根是2B．81的平方根是±3
C．8的立方根是±2D．立方根等于－1的实数是－1
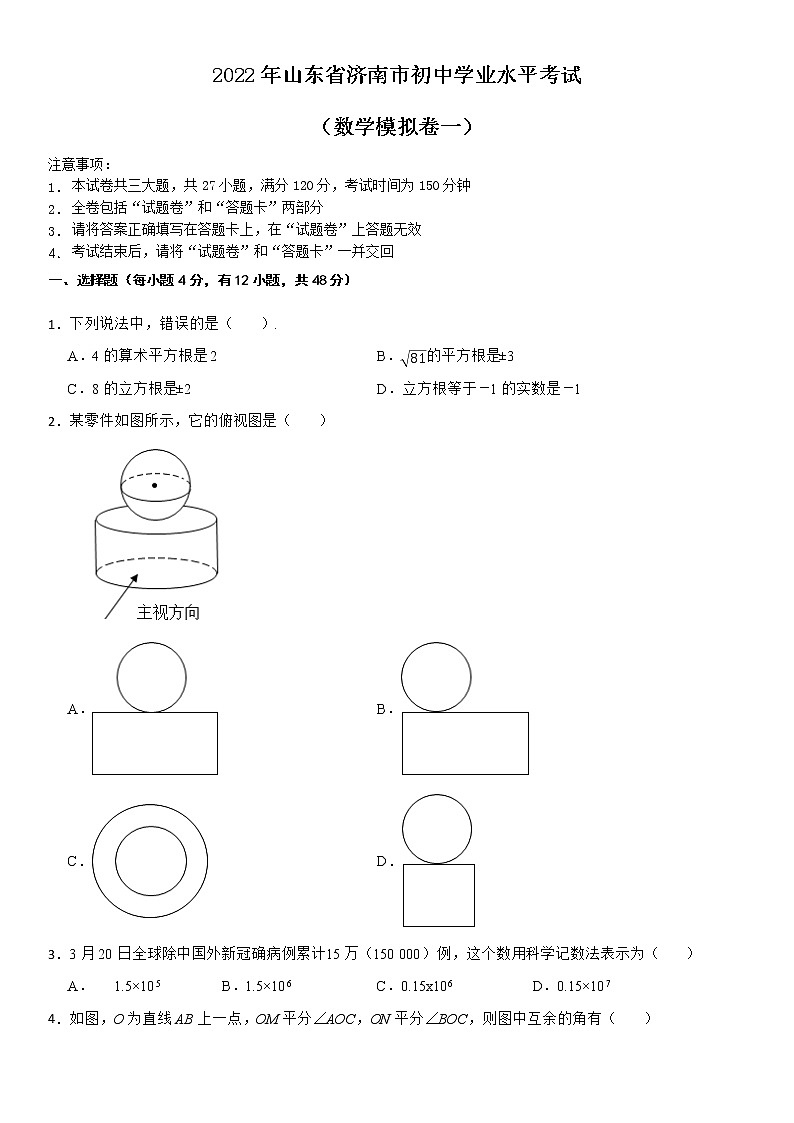
2．某零件如图所示，它的俯视图是（ ）
A．B．
C．D．
3．3月20日全球除中国外新冠确病例累计15万（150 000）例，这个数用科学记数法表示为（ ）
A． 1.5×105B．1.5×106C．0.15x106D．0.15×107
4．如图，O为直线AB上一点，OM平分∠AOC，ON平分∠BOC，则图中互余的角有（ ）
A．4对B．3对C．2对D．1对
5．下列图案中不是轴对称图形的是（ ）
A．B．
C．D．
6．实数a，b在数轴上对应点的位置如图所示，且|a|＞|b|，则化简 a2 ＋|a＋b|的结果为（ ）
A．2a＋bB．﹣2a﹣bC．bD．2a﹣b
7．计算 3x+2-1x-2+2xx2-4 ，结果正确的是（ ）
A．2x-2B．4x-2 C．2x+2 D．4x+2
8．一个仅装有球的不透明布袋里共有3个球（只有颜色不同），其中2个是红球，1个是黄球，从中任意摸出一个球，记下颜色后放回，搅匀，再摸出一个球，记下颜色，则摸出的2个球颜色相同的概率是（ ）
A．29B．13C．49D．59
9．下列函数的图象，一定经过原点的是（ ）
A．y=x2－1B．y=3x2－2xC．y=2x+1D．y=2x
10．3月中旬某中学校园内的樱花树正值盛花期，供全校师生驻足观赏. 如图，有一棵樱花树AB垂直于水平平台BC，通往平台有一斜坡CD，D，E在同一水平地面上，A，B，C，D，E均在同一平面内，已知BC＝3米，CD＝5米，DE＝1米，斜坡CD的坡度是 34 ，李同学在水平地面E处测得树冠顶端A的仰角为62°，则樱花树的高度AB约为（ ）（参考数据：sin62°≈0.88，cs62°≈0.47，tan62°≈1.88）
A． 9.16米B．12.04米C．13.16米D．15.04米
11．如图，菱形ABCD的四个顶点均在坐标轴上，对角线AC、BD交于原点O，DF⊥AB交AC于点G，反比例函数y＝ 3x （x＞0）经过线段DC的中点E，若BD＝4，则AG的长为（ ）
A．433B．3 +2C．2 3 +1D．332 +1
12．如图， Rt△ABC 中， ∠ACB=90° ， ∠ABC=30° ， AC=6 ，D是线段AB上一个动点，以BD为边在 △ABC 外作等边 △BDE .若F是DE的中点，则CF的最小值为（ ）
A．6 B．8C．9 D．10
二、填空题（每小题4分，共6小题，共24分）
13．因式分解：m3n﹣4m2n2+4mn3＝ .
14．如图，在△ABC中，∠ACB=90°，AB=10，AC=8，P是AB边上的动点（不与点B重合），点B关于直线CP的对称点是B′，连接B′A，则B′A长度的最小值是 ．
15．如图，以正六边形ADHGFE的一边AD为边向外作正方形ABCD，则∠BED＝ ．
16．若关于x的一元二次方程 x2-bx+2=0 有一个根为1，则方程另一个根为 .
17．如图，反比例函数y=kx（k≠0）与正比例函数y＝mx（m≠0）的图像交于点A，点B．AC⊥x轴于点C，BD⊥x轴于点D，S△ACO+S△BDO=2，则k＝__．
18．如图，AC = BC = BF = FG，∠ACB = ∠BFG = 90°，C，B，G三点共线，AG，CF相交于点K，CF交AB于点M，AG交BF于点N，则下列结论正确的是 （填序号）.
①△CBF∽△ABG：②CK = 12 AG；③BC2 = GC·BK；④∠AGC = ∠KBN = 22.5°
三、解答题（共9小题，共78分）
19．计算： 2sin60°-|1-3|-(-1)2021-2-2.
20．解不等式组 x+3>52x-321．如图：△ABC与△DEF中，边BC，EF在同一条直线上，AB∥DE，AC∥DF，且BF＝CE，求证：AC＝DF．
22．现有甲、乙、丙三名学生参加学校演讲比赛，并通过抽签确定三人演讲的先后顺序．
（1）求甲第一个演讲的概率；
（2）画树状图或表格，求丙比甲先演讲的概率．
23．如图，将△ABC绕点A按顺时针方向旋转90°，得到△ADE，点B的对应点为点D，点C的对应点E落在BC边上，连接BD.
（1）求证：DE⊥BC；
（2）若AC＝3 2 ，BC＝7，求线段BD的长.
24．新冠肺炎疫情期间，某口罩厂为生产更多的口罩满足疫情防控需求，决定拨款456万元购进A，B两种型号的口罩机共30台.两种型号口罩机的单价和工作效率分别如下表：
（1）求购进A，B两种型号的口罩生产线各多少台.
（2）现有200万只口罩的生产任务，计划安排新购进的口罩机共15台同时进行生产.若工厂的工人每天工作8h，则至少租用A种型号的口罩机多少台才能在5天内完成任务？
25．如图，已知在 △ABP 中， C 是 BP 边上一点， ∠PAC=∠PBA ， ⊙O 是 △ABC 的外接圆， AD 是 ⊙O 的直径，且交 BP 于点 E .
（1）求证： PA 是 ⊙O 的切线；
（2）过点 C 作 CF⊥AD ，垂足为点 F ，延长 CF 交 AB 于点 G ，若 AG·AB=48 ，求 AC 的长；
（3）在满足（2）的条件下，若 AF:FD=1:2 ， GF=2 ，求 ⊙O 的半径及 sin∠ACE 的值.
26．如图，在平面直角坐标系中，抛物线y=-2x2+bx+c与x轴交于点A(-3,0)、B，与y轴正半轴交于点C，OC=2OA，在直线AC上方的抛物线上有一动点E.
（1）求抛物线的解析式；
（2）连接BE，与直线AC相交于点F，当EF=12BF时，求点E的坐标；
（3）连接AE、CE、BC，四边形AECB的面积是否存在最大值？若存在，求出此时点E的坐标和四边形AECB的面积；若不存在，请说明理由.
27．如图，在平面直角坐标系xOy中，AB在x轴上，以AB为直径的半圆⊙O′与y轴正半轴交于点C，连接BC，AC.CD是半圆⊙O′的切线，AD⊥CD于点D.
（1）求证：∠CAD＝∠CAB.
（2）已知抛物线y＝ax2＋bx＋c过A、B、C三点，AB＝10，AO＝2CO.
①求抛物线的表达式；
②判断抛物线的顶点E是否在直线CD上，并说明理由.
参考答案
1．【答案】C
2．【答案】C
3．【答案】A
4．【答案】A
5．【答案】B
6．【答案】B
7．【答案】D
8．【答案】D
9．【答案】B
10．【答案】B
11．【答案】A
12．【答案】C
13．【答案】mn（m﹣2n）2
14．【答案】2
15．【答案】45°
16．【答案】2
17．【答案】-2
18．【答案】①②④
19．【答案】解：2sin60°-|1-3|-(-1)2021-2-2
=2×32-(3-1)-(-1)-14
=3-3+1+1-14
=74.
20．【答案】解： x+3>①2x-3解不等式①得： x>2
解不等式②得： x<5
所以，解不等式组的解集为： 2在数轴上表示为
21．【答案】证明：∵AB∥DE，
∴∠B＝∠E，
∵AC∥DF
∴∠ACB＝∠EFD，
∵BF＝CE
∴BC＝EF，且∠B＝∠E，∠ACB＝∠EFD，
∴△ABC≌△DEF（ASA）
∴AC＝DF
22．【答案】（1）解：甲第一个演讲的概率是 13
（2）解：树状图如下：
共有6种等可能情况，其中丙比甲先演讲的有3种，
∴P（丙比甲先演讲）= 36=12 .
23．【答案】（1）解：∵将△ABC绕点A按顺时针方向旋转90°，
∴AC＝AE，∠CAE＝90°，∠AED＝∠ACE，
∴∠ACE＝∠AEC＝45°＝∠AED，
∴∠DEC＝90°，
∴DE⊥BC
（2）解：∵AE＝AC＝3 2 ，∠EAC＝90°，
∴EC＝6，
∴BE＝BC﹣EC＝1，
∵将△ABC绕点A按顺时针方向旋转90°，
∴DE＝BC＝7，
∴DB＝ BE2+DE2 ＝ 492+12 ＝5 2 .
24．【答案】（1）解：设购进 A 种型号的生产线为 x 台，则购进 B 种型号的生产线为 (30-x) 台，
则： 16x+14.8(30-x)=456
解得： x=10 ，
所以： 30-x=20,
即购进A，B两种型号的口罩生产线分别为10台，20台.
（2）解：设至少租用A种型号的口罩机 m 台才能在5天内完成任务，则
5×8×0.4x+5×8×0.3(15-x)≥200
∴4x≥20,
解得： x≥5.
至少租用A种型号的口罩机5台才能在5天内完成任务.
25．【答案】（1）证明：连接CD，
∵AD是⊙O的直径，
∴∠ACD＝90°，
∴∠CAD＋∠ADC＝90°，
又∵∠PAC＝∠PBA，∠ADC＝∠PBA，
∴∠PAC＝∠ADC，
∴∠CAD＋∠PAC＝90°，即∠PAD=90°，
∴PA⊥OA.
又∵AD是⊙O的直径，
∴PA是⊙O的切线；
（2）解：由（1）知，PA⊥AD，
又∵CF⊥AD，
∴CF∥PA，
∴∠GCA＝∠PAC，
又∵∠PAC＝∠PBA，
∴∠GCA＝∠PBA，
又∵∠CAG＝∠BAC，
∴△CAG∽△BAC，
∴ACAB=AGAC ，即AC2＝AG•AB，
∵AG•AB＝48，
∴AC2＝48.
∴AC＝ 43 .
（3）解：设AF＝x，
∵AF：FD＝1：2，
∴FD＝2x.
∴AD＝AF＋FD＝3x.
在Rt△ACD中，
∵CF⊥AD，
由射影定理得：AC2＝AF•AD，
即3x2＝48.
解得；x＝4.
∴AF＝4，AD＝12.
∴⊙O半径为6.
在Rt△AFG中，∵AF＝4，GF＝2，
∴根据勾股定理得：AG＝ AF2+GF2=42+22=25 ，
由（2）知，AG•AB＝48，
∴AB＝ 48AG=2455 ，
连接BD，∵AD是⊙O的直径，
∴∠ABD＝90°.
在Rt△ABD中，
∵sin∠ADB＝ ABAD ，AD＝12，AB＝ 2455 ，
∴sin∠ADB＝ 255 .
∵∠ACE＝∠ACB＝∠ADB，
∴sin∠ACE＝ 255 .
26．【答案】（1）解：∵A(-3,0)，OC=2OA，
∴OA=3，OC=6，
∴C(0,6)，
把A(-3,0)，C(0,6)代入y=-2x2+bx+c，
得：-18-3b+c=0c=6，
解得：b=-4c=6，
∴抛物线的解析式为y=-2x2-4x+6；
（2）解：在y=-2x2-4x+6中，令y=0，
得：-2x2-4x+6=0，
解得：x1=-3，x2=1，
∴B(1,0)，
如图1，过点E作EH⊥AB于点H，过点F作FG⊥AB于点G，
则FG//EH，
∴ΔBFG∽ΔBEH，
∴BFBE=BGBH=FGEH，
∵EF=12BF，
∴BF=23BE，即BFBE=23，
∴BFBE=BGBH=FGEH=23，
设直线AC的解析式为y=kx+n(k≠0)，把A(-3,0)，C(0,6)代入得：
-3k+n=0n=6
解得： k=2n=6
∴直线AC的解析式为y=2x+6，
设E(t,-2t2-4t+6)，则BH=1-t，BG=23BH=23(1-t)，
∴OG=23(1-t)-1=-23t-13，
∴G(23t+13,0)，点F的横坐标为23t+13，
∵点F在直线AC：y=2x+6上，
∴点F的纵坐标为2(23t+13)+6=43t+203，
∴F(23t+13，43t+203)，
∴FG=43t+203，EH=-2t2-4t+6，
∵FGEH=23，
∴3FG=2EH，
∴3(43t+203)=2(-2t2-4t+6)，
解得：t1=-2，t2=-1，
当t=-2时，-2t2-4t+6=-2×(-2)2-4×(-2)+6=6，
∴E(-2,6)，
当t=-1时，-2t2-4t+6=-2×(-1)2-4×(-1)+6=8，
∴E(-1,8)，
综上所述，点E的坐标为(-2,6)或(-1,8)；
（3）解：四边形AECB的面积存在最大值.
∵S四边形AECB=SΔABC+SΔACE，
SΔABC=12AB⋅OC=12×4×6=12，
∴当SΔACE最大时，四边形AECB的面积最大，
设E(t,-2t2-4t+6)，作EH⊥AB于点H，交AC于点M，
∴M(t,2t+6)，
∴EM=-2t2-4t+6-(2t+6)=-2t2-6t，
∴SΔACE=SΔAME+SΔCEM=12×(-2t2-6t)×3=-3t2-9t=-3(t+32)2+274，
∴当t=-32时，SΔACE有最大值为274，
当t=-32时，-2t2-4t+6=-2×(-32)2-4×(-32)+6=152，
∴当点E的坐标为(-32，152)时，四边形AECB的面积有最大值为274+12=754.
27．【答案】（1）证明：连接O'C，
∵O'是圆心，
∴AO'＝CO'，
∴∠CAO＝∠CO'A，
∵CD是⊙O'的切线，
∴O'C⊥CD，
∵AD⊥CD，
∴O'C∥AD，
∴∠DAC＝∠ACO'，
∴∠CAD＝∠CAB；
（2）解：①∵∠ACB＝90°，∠AOC＝90°，
∴∠ACO＝∠CBA，
∴△ACO∽△CBO，
∴AOCO＝COBO，
∵AO＝2CO，
∴12CO＝BO，
∵AB＝10，
∴2CO＋12CO＝10，
∴CO＝4，
∴AO＝8，BO＝2，
∴A（﹣8，0），B（2，0），C（0，4），
设抛物线的解析式y＝a（x＋8）（x﹣2），将点C（0，2）代入，
∴4＝﹣16a，
∴a＝﹣14，
∴y＝﹣14x2﹣32x＋4；
②E点在直线CD上，理由如下：
y＝﹣14x2﹣32x＋4的顶点E（﹣3，254），
∵∠CO'G＋∠CGO'＝90°，∠CO'G＋∠O'CO＝90°，
∴∠CGO'＝∠OCO'，
∵OO'＝3，
∴tan∠CGO'＝tan∠OCO'，即OCOG＝OO'CO，
∴4OG＝34，
∴OG＝163，
∴G（163，0），
设直线CD的解析式为y＝kx＋b，
则有b=4163k+b=0，
∴k=-34b=4，
∴y＝﹣34x＋4，
当x＝3时，y＝254，
∴E点在直线CD上.

单价/万元
工作效率/（只/h）
A种型号
16
4000
B种型号
14.8
3000