2022年广东省揭阳市揭东区中考一模数学卷及答案（文字版）

这是一份2022年广东省揭阳市揭东区中考一模数学卷及答案（文字版），共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022年广东省揭阳市揭东区中考数学一模试卷
一、选择题（本大题共10小题，每小题3分，共30分）
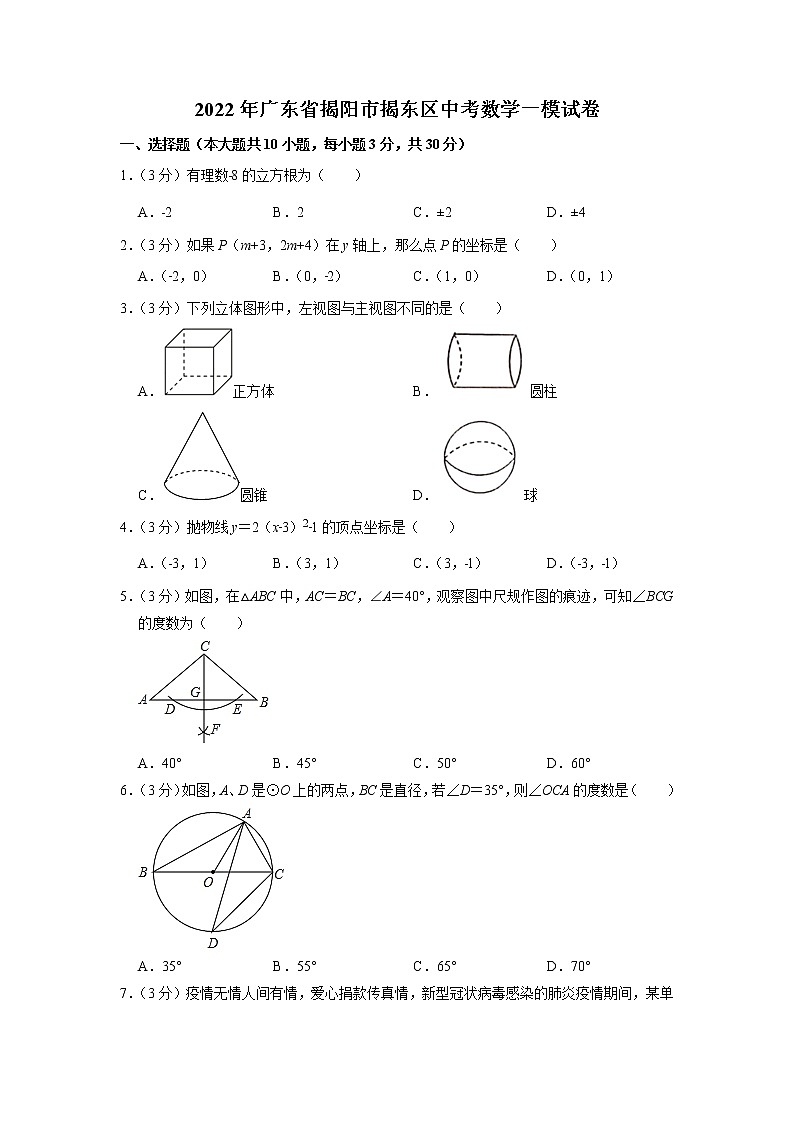
1．（3分）有理数﹣8的立方根为（　　）
A．﹣2 B．2 C．±2 D．±4
2．（3分）如果P（m+3，2m+4）在y轴上，那么点P的坐标是（　　）
A．（﹣2，0） B．（0，﹣2） C．（1，0） D．（0，1）
3．（3分）下列立体图形中，左视图与主视图不同的是（　　）
A．正方体 B．圆柱
C．圆锥 D．球
4．（3分）抛物线y＝2（x﹣3）2﹣1的顶点坐标是（　　）
A．（﹣3，1） B．（3，1） C．（3，﹣1） D．（﹣3，﹣1）
5．（3分）如图，在△ABC中，AC＝BC，∠A＝40°，观察图中尺规作图的痕迹，可知∠BCG的度数为（　　）

A．40° B．45° C．50° D．60°
6．（3分）如图，A、D是⊙O上的两点，BC是直径，若∠D＝35°，则∠OCA的度数是（　　）

A．35° B．55° C．65° D．70°
7．（3分）疫情无情人间有情，爱心捐款传真情，新型冠状病毒感染的肺炎疫情期间，某单位职工积极参加献爱心活动，该单位50名职工的捐款统计情况如下表：则他们捐款金额的众数和中位数分别是（　　）
金额
50
100
200
500
1000
人数
13
14
15
5
3
A．100，100 B．100，200 C．200，100 D．200，200
8．（3分）某公司今年4月的营业额为2500万元，按计划第二季度的总营业额要达到9100万元，设该公司5、6两月的营业额的月平均增长率为x．根据题意列方程，则下列方程正确的是（　　）
A．2500（1+x）2＝9100
B．2500（1+x%）2＝9100
C．2500（1+x）+2500（1+x）2＝9100
D．2500+2500（1+x）+2500（1+x）2＝9100
9．（3分）若关于x，y的方程组2x+y=4x+2y=−3m+2的解满足x﹣y＞−32，则m的最小整数解为（　　）
A．﹣3 B．﹣2 C．﹣1 D．0
10．（3分）二次函数y＝ax2+bx+c的部分图象如图所示，有以下结论：①3a﹣b＝0；②b2﹣4ac＞0；③5a﹣2b+c＞0；④4b+3c＞0，其中错误结论的个数是（　　）

A．1 B．2 C．3 D．4
二、填空题（本大题共7小题，每小题4分，共28分）
11．（4分）将数据1180000000用科学记数法表示为 　 　．
12．（4分）不等式3x+1＞2（x+4）的解为　 　．
13．（4分）已知等腰三角形的腰长、底边长分别是一元二次方程x2﹣7x+10＝0的两根，则该等腰三角形的周长是　 　．
14．（4分）如图，DE∥BC，EF∥AB，若AE：AC＝1：3，则DE：FC＝　 　．

15．（4分）如图，一艘轮船位于灯塔P的南偏东60°方向，距离灯塔50海里的A处，它沿正北方向航行一段时间后，到达位于灯塔P的北偏东45°方向上的B处，此时B处与灯塔P的距离为 　 　海里（结果保留根号）．

16．（4分）如图，将等边△AOB放在平面直角坐标系中，点A的坐标为（0，4），点B在第一象限，将等边△AOB绕点O顺时针旋转180°得到△A′OB′，则点B′的坐标是　 　．

17．（4分）如图，等边△ABC中，AB＝3，点D，点E分别是边BC，CA上的动点，且BD＝CE，连接AD、BE交于点F，当点D从点B运动到点C时，则点F的运动路径的长度为　 　．

三、解答题（一）（本大题共3小题，每小题6分，共18分）
18．（6分）解方程：2x−5x−2+3=3x−3x−2
19．（6分）先化简，再求值．
（5a+3ba2−b2+8bb2−a2）÷1a2b+ab2，其中a=2，b＝1．
20．（6分）将图中的A型（正方形）、B型（菱形）、C型（等腰直角三角形）纸片分别放在3个盒子中，盒子的形状、大小、质地都相同，再将这3个盒子装入一只不透明的袋子中．

（1）搅匀后从中摸出1个盒子，盒中的纸片既是轴对称图形又是中心对称图形的概率是　 　；
（2）搅匀后先从中摸出1个盒子（不放回），再从余下的2个盒子中摸出1个盒子，把摸出的2个盒中的纸片长度相等的边拼在一起，求拼成的图形是轴对称图形的概率．（不重叠无缝隙拼接）
四、解答题（二）（本大题共3小题，每小题8分，共24分）
21．（8分）如图，在平面直角坐标系xOy中，函数y＝﹣x+b的图象与函数y=kx（x＜0）的图象相交于点A（﹣1，6），并与x轴交于点C．点D是线段AC上一点，△ODC与△OAC的面积比为2：3．
（1）k＝　 　，b＝　 　；
（2）求点D的坐标．

22．（8分）为了提高农田利用效益，某地由每年种植双季稻改为先养殖小龙虾再种植一季水稻的“虾•稻”轮作模式．某农户有农田20亩，去年开始实施“虾•稻”轮作，去年出售小龙虾每千克获得的利润为32元（利润＝售价﹣成本）．由于开发成本下降和市场供求关系变化，今年每千克小龙虾的养殖成本下降25%，售价下降10%，出售小龙虾每千克获得利润为30元．
（1）求去年每千克小龙虾的养殖成本与售价；
（2）该农户今年每亩农田收获小龙虾100千克，若今年的水稻种植成本为600元/亩，稻谷售价为2.5元/千克，该农户估计今年可获得“虾•稻”轮作收入不少于8万元，则稻谷的亩产量至少会达到多少千克？
23．（8分）如图，在Rt△ABC中，∠A＝90°．AB＝8cm，AC＝6cm，若动点D从B出发，沿线段BA运动到点A为止（不考虑D与B，A重合的情况），运动速度为2cm/s，过点D作DE∥BC交AC于点E，连接BE，设动点D运动的时间为x（s），AE的长为y（cm）．
（1）求y关于x的函数表达式，并写出自变量x的取值范围；
（2）当x为何值时，△BDE的面积S有最大值？最大值为多少？

五、解答题（三）（本大题共2小题，每小题10分，共20分）
24．（10分）如图，⊙O是△ABC的外接圆，AB是直径，D是AC中点，直线OD与⊙O相交于E，F两点，P是⊙O外一点，P在直线OD上，连接PA，PC，AF，且满足∠PCA＝∠ABC．
（1）求证：PA是⊙O的切线；
（2）证明：EF2＝4OD•OP；
（3）若BC＝8，tan∠AFP=23，求DE的长．

25．（10分）已知抛物线y＝ax2+bx+3与x轴分别交于A（﹣3，0），B（1，0）两点，与y轴交于点C．点F是线段AD上一个动点．求：
（1）求抛物线的表达式及顶点D的坐标；
（2）如图1，设k=AFAD，当k为何值时，CF=12AD？
（3）如图2，以A，F，O为顶点的三角形是否与△ABC相似？若相似，求出点F的坐标；若不相似，请说明理由．


参考答案与解析
一、选择题（本大题共10小题，每小题3分，共30分）
1．（3分）有理数﹣8的立方根为（　　）
A．﹣2 B．2 C．±2 D．±4
【分析】利用立方根定义计算即可得到结果．
【解答】解：有理数﹣8的立方根为3−8=−2．
故选：A．
2．（3分）如果P（m+3，2m+4）在y轴上，那么点P的坐标是（　　）
A．（﹣2，0） B．（0，﹣2） C．（1，0） D．（0，1）
【分析】根据点在y轴上，可知P的横坐标为0，即可得m的值，再确定点P的坐标即可．
【解答】解：∵P（m+3，2m+4）在y轴上，
∴m+3＝0，
解得m＝﹣3，2m+4＝﹣2，
∴点P的坐标是（0，﹣2）．
故选：B．
3．（3分）下列立体图形中，左视图与主视图不同的是（　　）
A．正方体 B．圆柱
C．圆锥 D．球
【分析】从正面看所得到的图形是主视图，从左面看到的图形是左视图，进而分别判断得出答案．
【解答】解：A．左视图与主视图都是正方形，故选项A不合题意；
B．左视图是圆，主视图都是矩形，故选项B符合题意；
C．左视图与主视图都是三角形；故选项C不合题意；
D．左视图与主视图都是圆，故选项D不合题意；
故选：B．
4．（3分）抛物线y＝2（x﹣3）2﹣1的顶点坐标是（　　）
A．（﹣3，1） B．（3，1） C．（3，﹣1） D．（﹣3，﹣1）
【分析】直接根据二次函数的顶点式进行解答即可．
【解答】解：∵抛物线的解析式为：y＝2（x﹣3）2﹣1，
∴其顶点坐标为：（3，﹣1）．
故选：C．
5．（3分）如图，在△ABC中，AC＝BC，∠A＝40°，观察图中尺规作图的痕迹，可知∠BCG的度数为（　　）

A．40° B．45° C．50° D．60°
【分析】利用等腰三角形的性质和基本作图得到CG⊥AB，则CG平分∠ACB，利用∠A＝∠B和三角形内角和计算出∠ACB，从而得到∠BCG的度数．
【解答】解：由作法得CG⊥AB，
∵AC＝BC，
∴CG平分∠ACB，∠A＝∠B，
∵∠ACB＝180°﹣40°﹣40°＝100°，
∴∠BCG=12∠ACB＝50°．
故选：C．
6．（3分）如图，A、D是⊙O上的两点，BC是直径，若∠D＝35°，则∠OCA的度数是（　　）

A．35° B．55° C．65° D．70°
【分析】根据同弧所对的圆周角是圆心角的一半，可知∠AOC＝2∠D，求出∠AOC＝70°，由于OA＝OC，可知△AOC为等腰三角形，易求出∠OCA的度数．
【解答】解：∵∠AOC＝2∠D，∠D＝35°，
∴∠AOC＝2∠D＝2×35°＝70°，
在等腰△OAC中，∵OA＝OC，∠AOC＝70°，
∴∠OCA=180°−70°2=55°，
故选：B．
7．（3分）疫情无情人间有情，爱心捐款传真情，新型冠状病毒感染的肺炎疫情期间，某单位职工积极参加献爱心活动，该单位50名职工的捐款统计情况如下表：则他们捐款金额的众数和中位数分别是（　　）
金额
50
100
200
500
1000
人数
13
14
15
5
3
A．100，100 B．100，200 C．200，100 D．200，200
【分析】根据众数和中位数的定义求解即可．
【解答】解：捐款金额200出现的次数最多，故众数是200；
共有数据50个，第25个数和第26个数都是100，所以中位数是100．
故选：C．
8．（3分）某公司今年4月的营业额为2500万元，按计划第二季度的总营业额要达到9100万元，设该公司5、6两月的营业额的月平均增长率为x．根据题意列方程，则下列方程正确的是（　　）
A．2500（1+x）2＝9100
B．2500（1+x%）2＝9100
C．2500（1+x）+2500（1+x）2＝9100
D．2500+2500（1+x）+2500（1+x）2＝9100
【分析】分别表示出5月，6月的营业额进而得出等式即可．
【解答】解：设该公司5、6两月的营业额的月平均增长率为x．根据题意列方程得：
2500+2500（1+x）+2500（1+x）2＝9100．
故选：D．
9．（3分）若关于x，y的方程组2x+y=4x+2y=−3m+2的解满足x﹣y＞−32，则m的最小整数解为（　　）
A．﹣3 B．﹣2 C．﹣1 D．0
【分析】方程组中的两个方程相减得出x﹣y＝3m+2，根据已知得出不等式，求出不等式的解集即可．
【解答】解：2x+y=4①x+2y=−3m+2②，
①﹣②得：x﹣y＝3m+2，
∵关于x，y的方程组2x+y=4x+2y=−3m+2的解满足x﹣y＞−32，
∴3m+2＞−32，
解得：m＞−76，
∴m的最小整数解为﹣1，
故选：C．
10．（3分）二次函数y＝ax2+bx+c的部分图象如图所示，有以下结论：①3a﹣b＝0；②b2﹣4ac＞0；③5a﹣2b+c＞0；④4b+3c＞0，其中错误结论的个数是（　　）

A．1 B．2 C．3 D．4
【分析】①对称轴为x=−32，得b＝3a；
②函数图象与x轴有两个不同的交点，得Δ＝b2﹣4ac＞0；
③当x＝﹣1时，a﹣b+c＞0，当x＝﹣3时，9a﹣3b+c＞0，得5a﹣2b+c＞0；
④由对称性可知x＝1时对应的y值与x＝﹣4时对应的y值相等，当x＝1时a+b+c＜0，4b+3c＝3b+b+3c＝3b+3a+3c＝3（a+b+c）＜0；
【解答】解：由图象可知a＜0，c＞0，对称轴为x=−32，
∴x=−32=−b2a，
∴b＝3a，
①正确；
∵函数图象与x轴有两个不同的交点，
∴Δ＝b2﹣4ac＞0，
②正确；
当x＝﹣1时，a﹣b+c＞0，
当x＝﹣3时，9a﹣3b+c＞0，
∴10a﹣4b+2c＞0，
∴5a﹣2b+c＞0，
③正确；
由对称性可知x＝1时对应的y值与x＝﹣4时对应的y值相等，
∴当x＝1时a+b+c＜0，
∵b＝3a，
∴4b+3c＝3b+b+3c＝3b+3a+3c＝3（a+b+c）＜0，
∴4b+3c＜0，
④错误；
故选：A．
二、填空题（本大题共7小题，每小题4分，共28分）
11．（4分）将数据1180000000用科学记数法表示为 　1.18×109　．
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．
【解答】解：1 80000000＝1.18×109．
故答案是：1.18×109．
12．（4分）不等式3x+1＞2（x+4）的解为　x＞7　．
【分析】根据解一元一次不等式基本步骤：去括号、移项、合并同类项、系数化为1可得．
【解答】解：3x+1＞2（x+4），
3x+1＞2x+8，
x＞7．
故答案为：x＞7．
13．（4分）已知等腰三角形的腰长、底边长分别是一元二次方程x2﹣7x+10＝0的两根，则该等腰三角形的周长是　12　．
【分析】用因式分解法求出方程的两个根分别是2和5，有三角形的三边关系，2为底，5为腰，可以求出三角形的周长．
【解答】解：（x﹣2）（x﹣5）＝0
∴x1＝2，x2＝5．
因为三角形是等腰三角形，必须满足三角形三边的关系，
所以腰长是5，底边是2，周长为：
5+5+2＝12．
故答案是：12．
14．（4分）如图，DE∥BC，EF∥AB，若AE：AC＝1：3，则DE：FC＝　1：2　．

【分析】由DE∥BC，EF∥AB，易证得△ADE∽△EFC，又由AE：AC＝1：3，根据相似三角形的对应边成比例，即可求得答案．
【解答】解：∵DE∥BC，EF∥AB，
∴∠ADE＝∠B，∠AEC＝∠C，∠EFC＝∠B，
∴∠ADE＝∠EFC，
∴△ADE∽△EFC，
∵AE：AC＝1：3，
∴AE：EC＝1：2，
∴DE：FC＝AE：EC＝1：2．
故答案为：1：2．
15．（4分）如图，一艘轮船位于灯塔P的南偏东60°方向，距离灯塔50海里的A处，它沿正北方向航行一段时间后，到达位于灯塔P的北偏东45°方向上的B处，此时B处与灯塔P的距离为 　256　海里（结果保留根号）．

【分析】过点P作PC⊥AB，在Rt△APC中由锐角三角函数定义求出PC的长，再在Rt△BPC中由锐角三角函数定义求出PB的长即可．
【解答】解：过P作PC⊥AB于C，如图所示：
由题意得：∠APC＝30°，∠BPC＝45°，PA＝50海里，
在Rt△APC中，cos∠APC=PCPA，
∴PC＝PA•cos∠APC＝50×32=253（海里），
在Rt△PCB中，cos∠BPC=PCPB，
∴PB=PCcos∠BPC=25322=256（海里），
故答案为：256．

16．（4分）如图，将等边△AOB放在平面直角坐标系中，点A的坐标为（0，4），点B在第一象限，将等边△AOB绕点O顺时针旋转180°得到△A′OB′，则点B′的坐标是　（﹣23，﹣2）　．

【分析】作BH⊥y轴于H，如图，利用等边三角形的性质得到OH＝AH＝2，∠BOA＝60°，再计算出BH，从而得到B点坐标为（23，2），然后根据关于原点对称的点的坐标特征求出点B′的坐标．
【解答】解：作BH⊥y轴于H，如图，
∵△OAB为等边三角形，
∴OH＝AH＝2，∠BOA＝60°，
∴BH=3OH＝23，
∴B点坐标为（23，2），
∵等边△AOB绕点O顺时针旋转180°得到△A′OB′，
∴点B′的坐标是（﹣23，﹣2）．
故答案为（﹣23，﹣2）．

17．（4分）如图，等边△ABC中，AB＝3，点D，点E分别是边BC，CA上的动点，且BD＝CE，连接AD、BE交于点F，当点D从点B运动到点C时，则点F的运动路径的长度为　23π3．　．

【分析】根据已知条件证明△ABD≌△BCE，再得∠AFB＝120°，可得点F的运动轨迹是以点O为圆心，OA为半径的弧，此时∠AOB＝120°，OA=3，根据弧长公式即可得点F的运动路径的长度．
【解答】解：∵△ABC是等边三角形，
∴AB＝BC＝AC，∠ABC＝∠BAC＝∠BCE＝60°，
∴在△ABD和△BCE中，
AB=BC∠ABC=∠BCEBD=CE，
∴△ABD≌△BCE（SAS），
∴∠BAD＝∠CBE，
∵∠AFE＝∠BAD+∠FBA＝∠CBE+∠FBA＝∠ABC＝60°，
∴∠AFB＝120°，
∴点F的运动轨迹是以点O为圆心，OA为半径的弧，
如图，

此时∠AOB＝120°，OA=AHcos30°=3，
所以弧AB的长为：120π×3180=23π3．
则点F的运动路径的长度为23π3．
故答案为：23π3．
三、解答题（一）（本大题共3小题，每小题6分，共18分）
18．（6分）解方程：2x−5x−2+3=3x−3x−2
【分析】先把分式方程转化成整式方程，求出整式方程的解，再进行检验即可．
【解答】解：去分母，得：2x﹣5+3（x﹣2）＝3x﹣3，
去括号，得：2x﹣5+3x﹣6＝3x﹣3，
移项，合并，得：2x＝8，
系数化为1，得：x＝4，
经检验，当x＝4时，x﹣2≠0，即x＝4是原分式方程的解，
所以原方程的解是x＝4．
19．（6分）先化简，再求值．
（5a+3ba2−b2+8bb2−a2）÷1a2b+ab2，其中a=2，b＝1．
【分析】根据分式的运算法则即可求出答案．
【解答】解：原式=5a+3b−8ba2−b2÷1ab(a+b)
=5(a−b)(a+b)(a−b)•ab（a+b）
＝5ab，
当a=2，b＝1时，
原式＝52．
20．（6分）将图中的A型（正方形）、B型（菱形）、C型（等腰直角三角形）纸片分别放在3个盒子中，盒子的形状、大小、质地都相同，再将这3个盒子装入一只不透明的袋子中．

（1）搅匀后从中摸出1个盒子，盒中的纸片既是轴对称图形又是中心对称图形的概率是　23　；
（2）搅匀后先从中摸出1个盒子（不放回），再从余下的2个盒子中摸出1个盒子，把摸出的2个盒中的纸片长度相等的边拼在一起，求拼成的图形是轴对称图形的概率．（不重叠无缝隙拼接）
【分析】（1）依据搅匀后从中摸出1个盒子，可能为A型（正方形）、B型（菱形）或C型（等腰直角三角形）这3种情况，其中既是轴对称图形又是中心对称图形的有2种，即可得到盒中的纸片既是轴对称图形又是中心对称图形的概率；
（2）依据共有6种等可能的情况，其中拼成的图形是轴对称图形的情况有2种：A和C，C和A，即可得到拼成的图形是轴对称图形的概率．
【解答】解：（1）搅匀后从中摸出1个盒子，可能为A型（正方形）、B型（菱形）或C型（等腰直角三角形）这3种情况，其中既是轴对称图形又是中心对称图形的有2种，
∴盒中的纸片既是轴对称图形又是中心对称图形的概率是23；
故答案为：23；
（2）画树状图为：

共有6种等可能的情况，其中拼成的图形是轴对称图形的情况有2种：A和C，C和A，
∴拼成的图形是轴对称图形的概率为26=13．
四、解答题（二）（本大题共3小题，每小题8分，共24分）
21．（8分）如图，在平面直角坐标系xOy中，函数y＝﹣x+b的图象与函数y=kx（x＜0）的图象相交于点A（﹣1，6），并与x轴交于点C．点D是线段AC上一点，△ODC与△OAC的面积比为2：3．
（1）k＝　﹣6　，b＝　5　；
（2）求点D的坐标．

【分析】（1）将点A分别代入一次函数和反比例函数求解可得：
（2）过点D作DM⊥x轴，垂足为M，过点A作AN⊥x轴，垂足为N，根据面积的比得到DM和AN的比，求出DM的长，即点D纵坐标，从而求解．
【解答】解：（1）将点A（﹣1，6）代入y＝﹣x+b，
得6＝1+b，
解得b＝5，
将点A（﹣1.6）代入y=kx得，6=k−1，
∴k＝﹣6，
故答案为：﹣6，5；
（2）如图，过点D作DM⊥x轴，垂足为M，过点A作AN⊥x轴，垂足为N，

∵S△ODCS△OAC=12OC⋅DM12OC⋅AN=23，
∴DMAN=23，
∵点A的坐标为（﹣1，6），
∴AN＝6，
∴DM＝4，即点D的纵坐标为4，
把y＝4代入y＝﹣x+5中，
得x＝1，
∴点D（1，4）．
22．（8分）为了提高农田利用效益，某地由每年种植双季稻改为先养殖小龙虾再种植一季水稻的“虾•稻”轮作模式．某农户有农田20亩，去年开始实施“虾•稻”轮作，去年出售小龙虾每千克获得的利润为32元（利润＝售价﹣成本）．由于开发成本下降和市场供求关系变化，今年每千克小龙虾的养殖成本下降25%，售价下降10%，出售小龙虾每千克获得利润为30元．
（1）求去年每千克小龙虾的养殖成本与售价；
（2）该农户今年每亩农田收获小龙虾100千克，若今年的水稻种植成本为600元/亩，稻谷售价为2.5元/千克，该农户估计今年可获得“虾•稻”轮作收入不少于8万元，则稻谷的亩产量至少会达到多少千克？
【分析】（1）设去年每千克小龙虾的养殖成本与售价分别为x元、y元，由题意列出方程组，解方程组即可；
（2）设今年稻谷的亩产量为z千克，由题意列出不等式，解不等式即可．
【解答】解：（1）设去年每千克小龙虾的养殖成本与售价分别为x元、y元，
由题意得：y−x=32(1−10%)y−(1−25%)x=30，
解得：x=8y=40；
答：去年每千克小龙虾的养殖成本与售价分别为8元、40元；
（2）设今年稻谷的亩产量为z千克，
由题意得：20×100×30+20×2.5z﹣20×600≥80000，
解得：z≥640；
答：稻谷的亩产量至少会达到640千克．
23．（8分）如图，在Rt△ABC中，∠A＝90°．AB＝8cm，AC＝6cm，若动点D从B出发，沿线段BA运动到点A为止（不考虑D与B，A重合的情况），运动速度为2cm/s，过点D作DE∥BC交AC于点E，连接BE，设动点D运动的时间为x（s），AE的长为y（cm）．
（1）求y关于x的函数表达式，并写出自变量x的取值范围；
（2）当x为何值时，△BDE的面积S有最大值？最大值为多少？

【分析】（1）由平行线得△ABC∽△ADE，根据相似形的性质得关系式；
（2）由S=12•BD•AE；得到函数解析式，然后运用函数性质求解．
【解答】解：（1）动点D运动x秒后，BD＝2x．
又∵AB＝8，∴AD＝8﹣2x．
∵DE∥BC，
∴ADAB=AEAC，
∴AE=6(8−2x)8=6−32x，
∴y关于x的函数关系式为y=−32x+6（0＜x＜4）．
（2）解：S△BDE=12⋅BD⋅AE=12×2x(−32x+6)=−32x2+6x（0＜x＜4）．
当x=−62×(−32)=2时，S△BDE最大，最大值为6cm2．
五、解答题（三）（本大题共2小题，每小题10分，共20分）
24．（10分）如图，⊙O是△ABC的外接圆，AB是直径，D是AC中点，直线OD与⊙O相交于E，F两点，P是⊙O外一点，P在直线OD上，连接PA，PC，AF，且满足∠PCA＝∠ABC．
（1）求证：PA是⊙O的切线；
（2）证明：EF2＝4OD•OP；
（3）若BC＝8，tan∠AFP=23，求DE的长．

【分析】（1）先判断出PA＝PC，得出∠PAC＝∠PCA，再判断出∠ACB＝90°，得出∠CAB+∠CBA＝90°，再判断出∠PCA+∠CAB＝90°，得出∠CAB+∠PAC＝90°，即可得出结论；
（2）先判断出Rt△AOD∽Rt△POA，得出OA2＝OP•OD，进而得出14EF2＝OP•OD，即可得出结论；
（3）在Rt△ADF中，设AD＝2a，得出DF＝3a．OD=12BC＝4，AO＝OF＝3a﹣4，最后用勾股定理得出OD2+AD2＝AO2，即可得出结论．
【解答】（1）证明∵D是弦AC中点，
∴OD⊥AC，
∴PD是AC的中垂线，
∴PA＝PC，
∴∠PAC＝∠PCA．
∵AB是⊙O的直径，
∴∠ACB＝90°，
∴∠CAB+∠CBA＝90°．
又∵∠PCA＝∠ABC，
∴∠PCA+∠CAB＝90°，
∴∠CAB+∠PAC＝90°，即AB⊥PA，
∴PA是⊙O的切线；

（2）证明：由（1）知∠ODA＝∠OAP＝90°，
∴Rt△AOD∽Rt△POA，
∴AOPO=DOAO，
∴OA2＝OP•OD．
又OA=12EF，
∴14EF2＝OP•OD，即EF2＝4OP•OD．

（3）解：在Rt△ADF中，设AD＝2a，则DF＝3a．
OD=12BC＝4，OE＝AO＝OF＝3a﹣4．
∵OD2+AD2＝AO2，即42+4a2＝（3a﹣4）2，解得a=245，
∴DE＝OE﹣OD＝3a﹣8=325．
25．（10分）已知抛物线y＝ax2+bx+3与x轴分别交于A（﹣3，0），B（1，0）两点，与y轴交于点C．点F是线段AD上一个动点．求：
（1）求抛物线的表达式及顶点D的坐标；
（2）如图1，设k=AFAD，当k为何值时，CF=12AD？
（3）如图2，以A，F，O为顶点的三角形是否与△ABC相似？若相似，求出点F的坐标；若不相似，请说明理由．

【分析】（1）将A、B两点的坐标代入二次函数解析式，用待定系数法即求出抛物线对应的函数表达式，可求得顶点D（﹣1，4）；
（2）由A、C、D三点的坐标求出AC2＝18，CD2＝2，AD2＝20，可得△ACD为直角三角形，若CF=12AD，则点F为AD的中点，可求出k的值；
（3）由条件可判断∠DAC＝∠OCB，则∠OAF＝∠ACB，若以A，F，O为顶点的三角形与△ABC相似，可分两种情况考虑：当∠AOF＝∠ABC或∠AOF＝∠CAB＝45°时，可分别求出点F的坐标．
【解答】解：（1）∵抛物线y＝ax2+bx+3过点A（﹣3，0），B（1，0），
∴9a−3b+3=0a+b+3=0，解得：a=−1b=−2，
∴抛物线解析式为y＝﹣x2﹣2x+3；
∵y＝﹣x2﹣2x+3＝﹣（x+1）2+4，
∴顶点D的坐标为（﹣1，4）；

（2）∵y＝﹣x2﹣2x+3，
∴C（0，3），
在Rt△AOC中，OA＝3，OC＝3，
∴AC2＝OA2+OC2＝18，
∵D（﹣1，4），C（0，3），A（﹣3，0），
∴CD2＝12+12＝2，
∴AD2＝22+42＝20，
∴AC2+CD2＝AD2，
∴△ACD为直角三角形，且∠ACD＝90°．
∵CF=12AD，
∴F为AD的中点，
∴k=AFAD=12，
∴当k=12时，CF=12AD；

（3）在Rt△ACD中，tan∠CAD=DCAC=232=13，
在Rt△OBC中，tan∠OCB=OBOC=13，
∴∠CAD＝∠OCB，
∵OA＝OC，
∴∠OAC＝∠OCA＝45°，
∴∠FAO＝∠ACB，
若以A，F，O为顶点的三角形与△ABC相似，则可分两种情况考虑：
当∠AOF＝∠ABC时，△AOF∽△CBA，

∴OF∥BC，
设直线BC的解析式为y＝kx+b，
∴k+b=0b=3，解得：k=−3b=3，
∴直线BC的解析式为y＝﹣3x+3，
∴直线OF的解析式为y＝﹣3x，
设直线AD的解析式为y＝mx+n，
∴−k+b=4−3k+b=0，解得：k=2b=6，
∴直线AD的解析式为y＝2x+6，
∴y=2x+6y=−3x，解得：x=−65y=185，
∴F（−65，185）；
当∠AOF＝∠CAB＝45°时，△AOF∽△CAB，

∵∠CAB＝45°，
∴OF⊥AC，
∴直线OF的解析式为y＝﹣x，
∴y=−xy=2x+6，解得：x=−2y=2，
∴F（﹣2，2）．
综合以上可得F点的坐标为（−65，185）或（﹣2，2）．