2022年湖南省怀化市中考数学考前模拟冲刺卷(word版含答案)

这是一份2022年湖南省怀化市中考数学考前模拟冲刺卷(word版含答案)，共20页。
2022年湖南省怀化市中考数学考前模拟冲刺卷
一．选择题（共10小题，满分40分，每小题4分）
1．（4分）下列说法正确的是（　　）
A．数轴上表示2的点与表示8的点之间的距离是10
B．数轴上表示﹣2的点与表示﹣8的点之间的距离是﹣10
C．数轴上表示﹣8的点与表示2的点之间的距离是10
D．数轴上表示﹣8的点与原点之间的距离是﹣8
2．（4分）在国内疫情持续好转、旅游产业复工复产的当下，迎来了2020中秋国庆黄金周．据统计，本次黄金周全国出游人数约为637000000人次．把数据637000000用科学记数法表示为（　　）
A．6.37×107 B．6.37×108 C．0.637×109 D．63.7×106
3．（4分）下列图形中，不是中心对称图形的是（　　）
A．平行四边形 B．长方形 C．菱形 D．五角星
4．（4分）关于x的方程（x﹣3）（x+2）＝p2（p为常数）的根的情况，下列结论中正确的是（　　）
A．两个正根 B．两个负根
C．一个正根，一个负根 D．无实数根
5．（4分）如图，正方体纸盒的三个侧面分别印有文字“铜”、“陵”、“市”，现在沿着它的棱剪开，展开成一个平面图形，这个正方体的平面展开图可以是（　　）

A． B．
C． D．
6．（4分）对于非零的两个有理数a，b，规定a⊕b=1b-1a，若2⊕（2x﹣1）＝0，则x的值为（　　）
A．56 B．54 C．32 D．-16
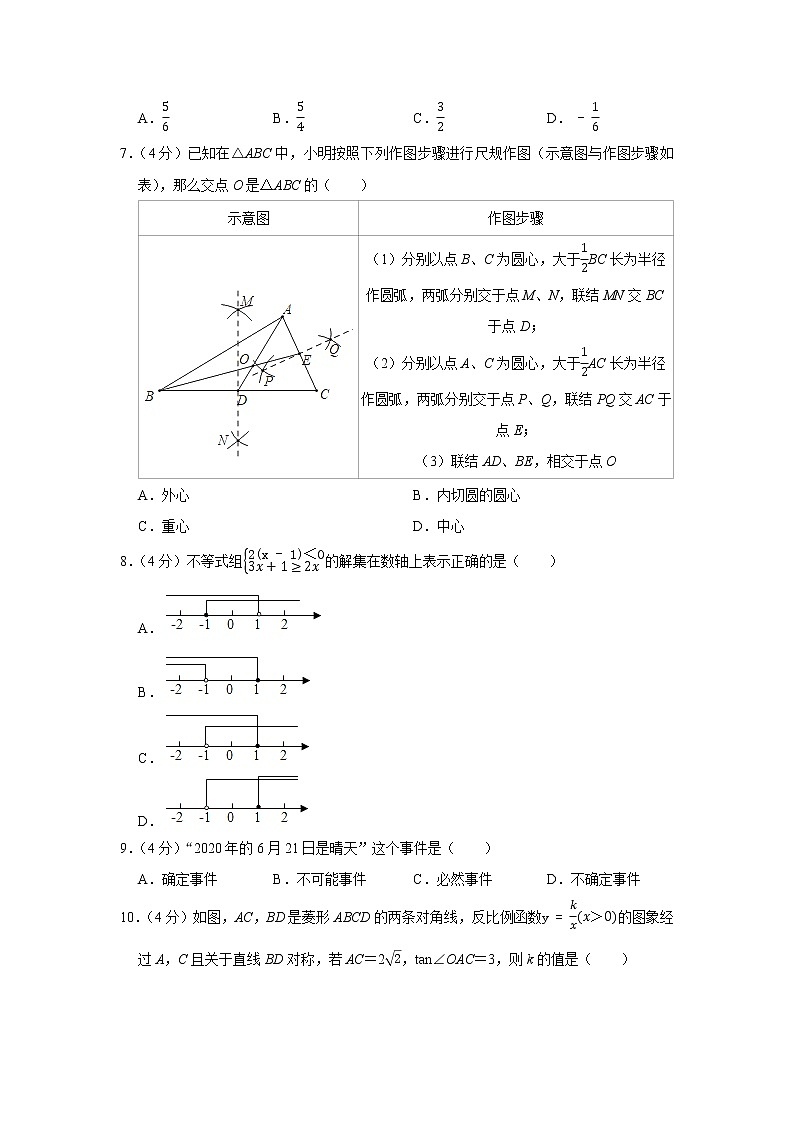
7．（4分）已知在△ABC中，小明按照下列作图步骤进行尺规作图（示意图与作图步骤如表），那么交点O是△ABC的（　　）
示意图
作图步骤


（1）分别以点B、C为圆心，大于12BC长为半径作圆弧，两弧分别交于点M、N，联结MN交BC于点D；
（2）分别以点A、C为圆心，大于12AC长为半径作圆弧，两弧分别交于点P、Q，联结PQ交AC于点E；
（3）联结AD、BE，相交于点O
A．外心 B．内切圆的圆心
C．重心 D．中心
8．（4分）不等式组2(x-1)＜03x+1≥2x的解集在数轴上表示正确的是（　　）
A．
B．
C．
D．
9．（4分）“2020年的6月21日是晴天”这个事件是（　　）
A．确定事件 B．不可能事件 C．必然事件 D．不确定事件
10．（4分）如图，AC，BD是菱形ABCD的两条对角线，反比例函数y=kx(x＞0)的图象经过A，C且关于直线BD对称，若AC＝22，tan∠OAC＝3，则k的值是（　　）

A．6 B．7 C．8 D．62
二．填空题（共6小题，满分24分，每小题4分）
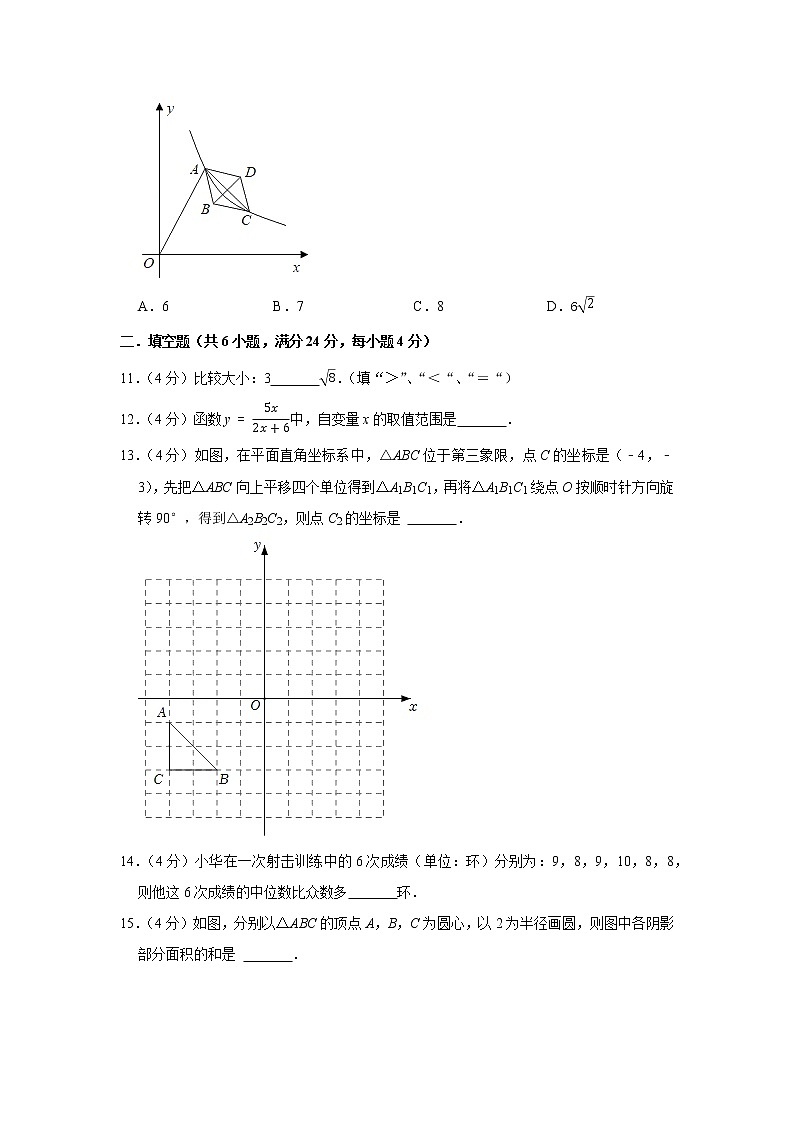
11．（4分）比较大小：3　 　8．（填“＞”、“＜“、“＝“）
12．（4分）函数y=5x2x+6中，自变量x的取值范围是　 　．
13．（4分）如图，在平面直角坐标系中，△ABC位于第三象限，点C的坐标是（﹣4，﹣3），先把△ABC向上平移四个单位得到△A1B1C1，再将△A1B1C1绕点O按顺时针方向旋转90°，得到△A2B2C2，则点C2的坐标是 　 　．

14．（4分）小华在一次射击训练中的6次成绩（单位：环）分别为：9，8，9，10，8，8，则他这6次成绩的中位数比众数多　 　环．
15．（4分）如图，分别以△ABC的顶点A，B，C为圆心，以2为半径画圆，则图中各阴影部分面积的和是 　 　．

16．（4分）寻找规律填空
（1）1×3+1＝22
（2）2×4+1＝32
（3）3×5+1＝42
…
请用含字母n的代数式描述上述规律：　 　．
三．解答题（共8小题，满分86分）
17．（8分）计算：﹣12021+（12021）0+2﹣1+3•tan30°．
18．（8分）计算：
（1）（48+418）﹣（313-20.5）；
（2）（3+2）2﹣（3-2）2；
（3）先化简，再求值：x+2x2-2x+1÷（3x+4x2-1-2x-1），其中x=2+1．
19．（10分）某中学数学实践小组利用节假日时间到现场测量一古建筑的牌匾悬挂的高度，如图1，大门上悬挂着巨大的匾额，图2中的线段BC就是悬挂在墙壁AM上的匾额的截面示意图．已知BC＝2米，∠MBC＝37°．他们在该古建筑底部所在的平地上，选取两个不同测量点D、E，分别测量了该牌匾端点的仰角以及这两个测量点之间的距离．为了减小测量误差，小组在测量仰角的度数以及两个测量点之间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如下表（不完整）．

测量数据
测量项目
第一次
第二次
平均值
∠ADC
43°
47°
45°
∠AEB
54.2°
51.8°
53°
D、E之间的距离
4.3m
4.5m

……
……
……
……
……
（1）D、E之间距离的平均值是 　 　．
（2）求匾额悬挂的高度AB的长．（参考数据：sin37°≈35，cos37°≈45，tan37°≈34）
20．（10分）如图，在平行四边形ABCD中，AC⊥BC，点E是CD的中点，连接AE，作AF⊥AE，交BC于点F．
（1）若AC＝6，BC＝8，求AE的长；
（2）若G为BC延长线上一点，且AG+CG＝BC，求证：AF＝2EG．

21．（12分）钟南山院士谈到防护新型冠状病毒肺炎时说：“我们需要重视防护，但也不必恐慌，尽量少去人员密集的场所，出门戴口罩，在室内注意通风，勤洗手，多运动，少熬夜．”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解，通过微信群宣传新型冠状病毒肺炎的防护知识，并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试（全国卷）》试卷（满分100分），社区管理员随机从有400人的某小区抽取40名人员的答卷成绩，并对他们的成绩（单位：分）统计如下：
85 80 95 100 90 95 85 65 75 85
90 90 70 90 100 80 80 90 95 75
80 60 80 95 85 100 90 85 85 80
95 75 80 90 70 80 95 75 100 90
根据数据绘制了如图的表格和统计图：
等级
成绩（x）
频数
频率
A
90＜x≤100
10
0.25
B
80＜x≤90
a
c
C
70＜x≤80
12
0.3
D
60≤x≤70
d
b
合计
40
1
根据上面提供的信息，回答下列问题：
（1）统计表中的a＝　 　，b＝　 　；c＝　 　，d＝　 　；
（2）请补全条形统计图；
（3）根据抽样调查结果，请估计该小区答题成绩为“C级”的有多少人？
（4）该社区有2名男管理员和2名女管理员，现从中随机挑选2名管理员参加“社区防控”宣传活动，请用树状图法或列表法求出恰好选中“1男1女”的概率．

22．（12分）如图，四边形ABCD内接于⊙O，AC是⊙O的直径，DE⊥BC交BC延长线于点E，CD平分∠ACE．
（1）求证DE是⊙O的切线；
（2）若AD＝6，DE＝4，求AC的长．

23．（12分）鹤峰县某茶叶加工企业，在助力精准扶贫行动中，推出惠农政策，连续用10天时间对清明前的毛尖鲜茶叶进行了收购，加工和销售．（当天收购的鲜茶叶，当天全部加工并销售完）经调查，整理出该茶叶经销商第x天（0＜x≤10，且x为整数）收购，加工和销售茶叶的相关信息如表：
鲜茶叶收购单价（元/kg）
200﹣10x
鲜茶叶收购量（kg）
110﹣10x
鲜茶叶加工后的成品茶重（kg）
33﹣3x
成品茶的销售单价元/kg）
900
（1）若经销商连续两天共收购鲜茶叶110kg，则这两天分别是第几天？
（2）该茶叶经销商在第几天的毛利润最大，最大值是多少？（当天毛利润＝成品茶销售金额﹣鲜茶叶收购金额）
（3）当该公司在获得日最大毛利润后，将该天的全部毛利润返还给的签约农户，用于生产发展资金，共返还三次，已知第三次返还给农户的金额为11664元，若每两次间返还金额的增长率a相同，求a的值．
24．（14分）如图，在平面直角坐标系中，一次函数y＝2x+4与x轴、y轴分别交于点D、E，二次函数y＝mx2﹣3mx﹣4m（m＜0）与x轴交于A、B两点．
（1）A点坐标　 　，B点坐标　 　；
（2）在x轴上方的抛物线上是否存在P点，使得以点A、B、P为顶点的三角形与△DEO相似？若存在，求m的值；若不存在，请说明理由；
（3）点Q为（2）中抛物线上的动点，当Q到直线DE距离最小时，求Q点坐标及最小值．


参考答案与试题解析
一．选择题（共10小题，满分40分，每小题4分）
1．【解答】解：选项A：8﹣2＝6，数轴上表示2的点与表示8的点之间的距离是6，而不是10，A不正确；
选项B：﹣2﹣（﹣8）＝﹣2+8＝6，数轴上表示﹣2的点与表示﹣8的点之间的距离是6，且距离不为负数，B不正确；
选项C：2﹣（﹣8）＝2+8＝10，数轴上表示﹣8的点与表示2的点之间的距离是10，是正确的；
选项D，0﹣（﹣8）＝8，数轴上表示﹣8的点与原点之间的距离是8，而不是﹣8，D不正确．
综上，只有C正确．
故选：C．
2．【解答】解：637000000＝6.37×108，
故选：B．
3．【解答】解：A．绕平行四边形的对角线的交点旋转180°后与原来的图形重合，所以平行四边形是中心对称图形，故本选项不合题意；
B．绕长方形的对角线的交点旋转180°后与原来的图形重合，所以长方形是中心对称图形，故本选项不合题意；
C．绕菱形的对角线的交点旋转180°后与原来的图形重合，所以菱形是中心对称图形，故本选项不合题意；
D．五角星不能找到这样的一个点，使五角星绕某一点旋转180°后与原来的图形重合，所以不是中心对称图形，故本选项符合题意．
故选：D．
4．【解答】解：∵（x﹣3）（x+2）＝p2（p为常数），
∴x2﹣x﹣6﹣p2＝0，
∴Δ＝b2﹣4ac＝1+24+4p2＝25+4p2＞0，
∴方程有两个不相等的实数根，
根据根与系数的关系，方程的两个根的积为﹣6﹣p2＜0，
∴一个正根，一个负根．
故选：C．
5．【解答】解：把四个选项的展开图折叠，能复原的是A．
故选：A．
6．【解答】解：根据题中的新定义化简2⊕（2x﹣1）＝0得：12x-1-12=0，
去分母得：2﹣2x+1＝0，
解得：x=32，
检验：把x=32代入得：2x﹣1≠0，
∴分式方程的解为x=32．
故选：C．
7．【解答】解：由尺规作图可知，MN、PQ分别是线段BC、AC的垂直平分线，
∴点D、E分别是BC、AC的中点，
∴AD、BE是△ABC的中线，
∴点O是△ABC的重心，
故选：C．
8．【解答】解：解不等式2（x﹣1）＜0，得：x＜1，
解不等式3x+1≥2x，得：x≥﹣1，
则不等式组的解集为﹣1≤x＜1，
故选：A．
9．【解答】解：“2020年的6月21日是晴天”这个事件是随机事件，属于不确定事件，
故选：D．
10．【解答】解：延长AC交x轴于点F，延长CA交y轴于点G，连接OC，过C作CH⊥OF于H，
设AC，BD交于点E，如图，

∵AC，BD是菱形ABCD的两条对角线，
∴BD⊥AC，AE＝EC=2．
∵反比例函数y=kx(x＞0)的图象关于直线BD对称，
∴直线BD经过原点O，且BD垂直平分线段GF．
∴OA＝OC，OG＝OF，∠OGF＝∠OFG＝45°．
∵tan∠OAC＝3，
∴OEAE=3．
∴OE＝3AE＝32．
∴EF＝EG＝OE＝32．
∴CF＝EF﹣EC＝22．
∵CH⊥HF，∠CFH＝45°，
∴CH=22CF＝2．
∵OC＝OA=OE2+AE2=25．
∴OH=OC2-CH2=4．
∴C（4，2）．
∵C在反比例函数y=kx(x＞0)的图象上，
∴k＝2×4＝8．
故选：C．
二．填空题（共6小题，满分24分，每小题4分）
11．【解答】解：∵4＜8＜9，
∴2＜8＜3，
∴3＞8．
故答案是：＞．
12．【解答】解：由题意，得2x+6≠0，
解得x≠﹣3．
故答案为：x≠﹣3．
13．【解答】解：如图，△A1B1C1，△A2B2C2即为所求．C2（1，4）．
故答案为：（1，4）．

14．【解答】解：这组数的众数为8环，中位数为8+92=8.5（环），
所以他这6次成绩的中位数比众数多0.5环，
故答案为：0.5．
15．【解答】解：∵⊙A、⊙B、⊙C的半径都是2，扇形的三个圆心角正好构成三角形的三个内角，
∴阴影部分扇形的圆心角度数为180°，
∴S绿色=180π×22360=2π．
故答案为：2π．
16．【解答】解：∵1×3+1＝22，2×4+1＝32，3×5+1＝42，
…
∴用含字母n的代数式描述上述规律：n×（n+2）+1＝（n+1）2．
故答案为：n×（n+2）+1＝（n+1）2．
三．解答题（共8小题，满分86分）
17．【解答】解：原式＝﹣1+1+12+3×33
＝﹣1+1+12+1
=32．
18．【解答】解：（1）（48+418）﹣（313-20.5）
＝（43+2）﹣（3-2）
＝43+2-3+2
＝33+22；
（2）（3+2）2﹣（3-2）2
＝3+26+2﹣（3﹣26+2）
＝3+26+2﹣3+26-2
＝46；
（3）x+2x2-2x+1÷（3x+4x2-1-2x-1）
=x+2(x-1)2÷3x+4-2(x+1)(x+1)(x-1)
=x+2(x-1)2⋅(x+1)(x-1)3x+4-2x-2
=x+2x-1⋅x+1x+2
=x+1x-1，
当x=2+1时，原式=2+1+12+1-1=1+2．
19．【解答】解：（1）D、E之间距离的平均值是12（4.3+4.5）＝4.4（m），
故答案为：4.4m；
（2）过点C作CN⊥AB，CF⊥AD，垂足分别为N、F，如图所示：
在Rt△BCN中，∠MBC＝37°，
CN＝BC•sin∠MBC≈2×35=1.2（米），
BN＝BC×cos37°≈2×45=1.6（米），
在Rt△ABE中，∠ABE＝90°﹣∠AEB＝90°﹣53°＝37°，
AE＝AB•tan∠ABE＝AB×tan37°＝AB×tan37°≈34AB，
∵∠ADC＝45°，
∴△CDF是等腰直角三角形，
∴CF＝DF，
∴BN+AB＝AD﹣AF＝AD﹣CN，
即：1.6+AB≈34AB+4.4﹣1.2，
解得：AB＝6.4（米），
答：匾额悬挂的高度AB的长约为6.4米．

20．【解答】（1）解：∵AC⊥BC，
∴∠ACB＝90°，
∵AC＝6，BC＝8，
∴AB=AC2+BC2=10，
∵四边形ABCD是平行四边形，
∴CD＝AB＝10，AD∥BC
∴CA⊥AD，
∴∠CAD＝90°，
∵CE＝ED，
∴AE=12CD＝5．
（2）证明：延长AE交BC的延长线于M，在CB上取一点N，使得CN＝CG，连接AN．

∵AD∥CM，
∴∠DAE＝∠M，
在△DAE和△MCE中，∠DAE=∠M∠AED=∠MECDE=CE，
∴△DAE≌△MCE（AAS），
∴AE＝EM，
∵AE＝ED＝EC，
∴AM＝CD＝AB，
∵AC⊥BM，
∴BC＝CM，
∵AC⊥NG，CN＝CG，
∴AG＝AN，
∵AG+CG＝BC，
∴BN＝AG＝AN，
∵CB＝CM，CN＝CG，
∴BN＝GM，
∴GA＝GM，
∵AE＝EM，
∴EG⊥AM，
∵FA⊥AM，
∴EG∥AF，
∵AE＝EM，
∴FG＝GM，
∴EG=12AF，
即AF＝2EG．
21．【解答】解：（1）由题意可知：B等级的频数a＝14，
∴B等级的频率：c＝14÷40＝0.35，
D等级的频数d＝40﹣10﹣14﹣12＝4，b＝1﹣0.25﹣0.35﹣0.3＝0.1．
故答案为：14，0.1，0.35，4；
（2）如图即为补全的条形统计图：

（3）0.3×400＝120（人），
答：估计该小区答题成绩为“C级”的有120人；
（4）画树状图如图：

根据树状图可知：所有等可能的结果共有12种，其中恰好选中“1男1女”的有8种，
∴恰好选中“1男1女”的概率为812=23．
22．【解答】（1）证明：连接OD，

∵DE⊥BC，
∴∠DEC＝90°，
∵OD＝OC，
∴∠OCD＝∠ODC，
∵CD平分∠ACE，
∴∠ACD＝∠DCE，
∴∠ODC＝∠DCE，
∴OD∥CE，
∴∠ODE+∠DEC＝180°，
∴∠ODE＝180°﹣∠DEC＝90°，
∵OD是⊙O的半径，
∴DE是⊙O的切线；
（2）解：∵AC是⊙O的直径，
∴∠ADC＝90°，
∵∠ADC＝∠DEC＝90°，∠ACD＝∠DCE，
∴△ADC∽△DEC，
∴ADDE=ACDC=64=32，
∴设AC＝3x，DC＝2x，
∵AD2+CD2＝AC2，
∴36+（2x）2＝（3x）2，
∴x=655或x=-655（舍去），
∴AC=1855．
23．【解答】解：（1）连续两天用x、x+1表示，则有：
（110﹣10x）+[110﹣10（x+1）]＝110，
解得x＝5，
∴这两天分别是第5天和第6天；
（2）设该经销商每日毛利润表示为y，
则y＝（33﹣3x）×900﹣（110﹣10x）（200﹣10x）
＝﹣100x2+400x+7700
＝﹣100（x﹣2）2+8100，
∵﹣100＜0，
∴当x＝2时，y有最大值，最大值为8100，
∴该茶叶经销商在第2天的毛利润最大，最大值是8100元；
（3）由题意可得
8100（1+a）2＝11664，
解得：a1＝20%，a2＝﹣2.2（舍去），
∴a 为20%．
24．【解答】解：（1）令y＝mx2﹣3mx﹣4m＝0，
解得x＝﹣1或4，
故点A、B的坐标分别为（﹣1，0）、（4，0），
故答案为（﹣1，0）、（4，0）；

（2）存在，理由：
对于一次函数y＝2x+4，令y＝2x+4＝0，则x＝﹣2，令x＝0，则y＝4，故点D、E的坐标分别为（﹣2，0）、（0，4），
在Rt△ODE中，tan∠EDO＝2，则sin∠EDO=25，
当以点A、B、P为顶点的三角形与△DEO相似时，只能是∠APB为直角，如图1，设点P的为（a，b），
∵OE：OD＝2，故以点A、B、P为顶点的三角形与△DEO相似时，两个三角形的相似比为2或12，
过点P作x轴的平行线，交过点A与y轴的平行线于点M，交过点B与y轴的平行线于点N，

∵∠MPA+∠BPN＝90°，∠BPN+∠PBN＝90°，
∴∠MPA＝∠PBN，
∵∠PMA＝∠BNP＝90°，
∴△PMA∽△BNP，且相似比为2或12，
即PMBN=AMPN=2或12，即ba+1=4-ab=2或12，
解得a=3b=2，则点P（3，2），
将点P的坐标代入y＝mx2﹣3mx﹣4m得：2＝9m﹣9m﹣4m，
解得m=-12；

（3）由（2）知，抛物线的表达式为y=-12x2+32x+2，
如图2，过点Q作x轴的平行线交DE于点N，则∠HNQ＝∠EDO，则sin∠HNQ＝sin∠EDO=25，
设点Q的坐标为（t，-12t2+32t+2），点N（x，2x+4），
∵y＝2x+4=-12t2+32t+2，则x=-14t2+34t﹣1，
过点Q作QH⊥DE于点H，则HQ为Q到直线DE距离，

HQ＝NQsin∠HNQ=25[t﹣（-14t2+34t﹣1）]=255（14t2+14t+1），
∵255×(14)＞0，故HQ有最小值，
当t=-12时，HQ有最小值为358，此时点Q（-12，98）．