第27讲-椭圆及其性质-【高考培优直通车】2022年高三数学大一轮复习精品讲义（上海专用）

这是一份第27讲-椭圆及其性质-【高考培优直通车】2022年高三数学大一轮复习精品讲义（上海专用），文件包含第27讲-椭圆及其性质解析版-高考培优直通车-2022年高三数学大一轮复习教案上海专用docx、第27讲-椭圆及其性质原卷版-高考培优直通车-2022年高三数学大一轮复习教案上海专用docx等2份试卷配套教学资源，其中试卷共55页， 欢迎下载使用。

第27讲-椭圆及其性质（解析版）
学习目标：


1．正确理解椭圆的定义，能运用定义解题，能根据条件，求出椭圆的标准方程
2．掌握椭圆的几何性质，明确从椭圆的范围、顶点坐标、对称性等方面.
3.了解椭圆的几何性质,并且应用相关性质解题, 培养学生数形结合的重要数学思想方法

教学内容


1．已知椭圆上一点到椭圆的一焦点的距离为，则到另一焦点的距离是（ ）
A． B． C． D．
【答案】C
【详解】椭圆上的点到两焦点的距离之和为，所以到另一焦点的距离为.
2．已知椭圆的焦点在轴上，若椭圆的短轴长为4，则的取值范围是( )
A． B． C． D．
【答案】A
【详解】依题意得，且，故选A.
3．如果表示焦点在轴上的椭圆，那么实数的取值范围是（ ）
A． B． C． D．
【答案】A
【详解】转化为椭圆的标准方程，得，因为表示焦点在轴上的椭圆，所以，解得.所以实数的取值范围是.选A.



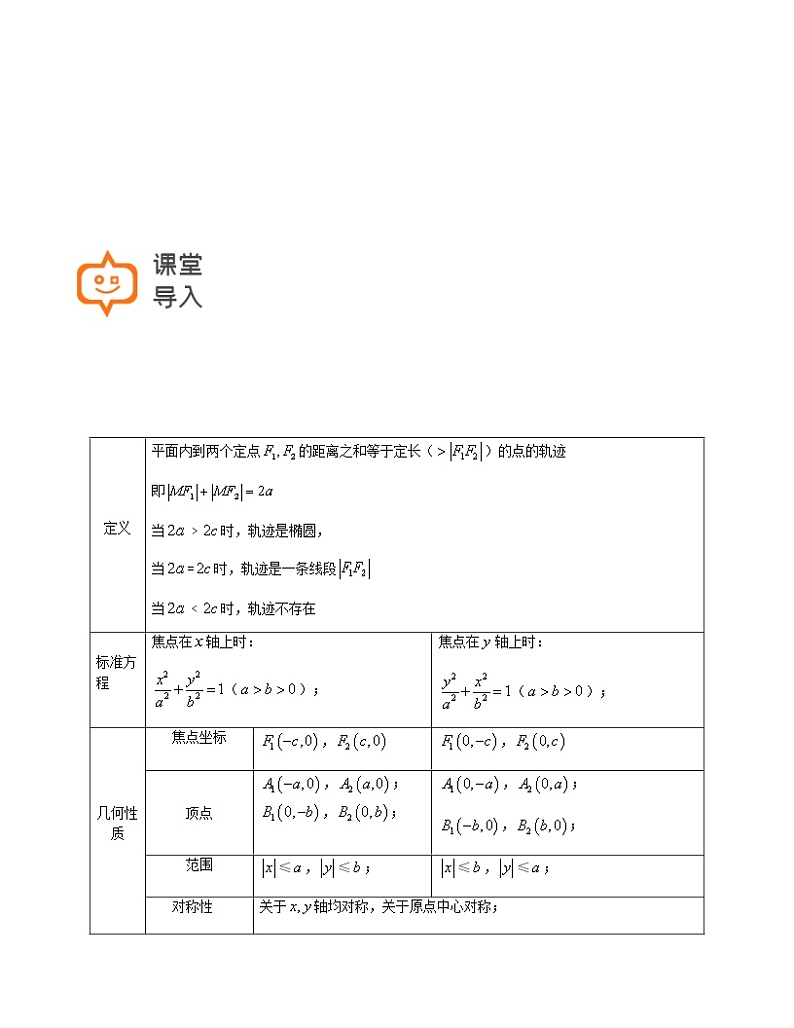
定义
平面内到两个定点的距离之和等于定长（）的点的轨迹
即
当﹥时，轨迹是椭圆，
当=时，轨迹是一条线段
当﹤时，轨迹不存在
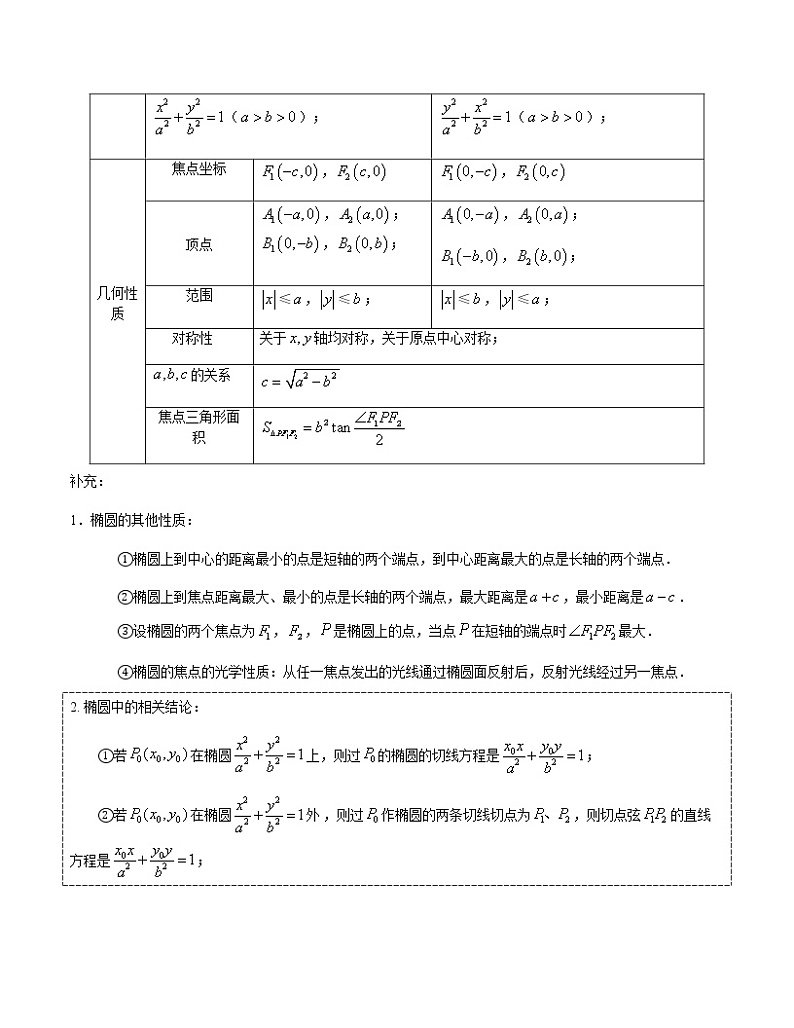
标准方 程
焦点在轴上时：
（）；
焦点在轴上时：
（）；
几何性质
焦点坐标
，
，

顶点
，； ，；
，；
，；
范围
≤，≤；
≤，≤；
对称性
关于轴均对称，关于原点中心对称；
的关系

焦点三角形面积

补充：
1．椭圆的其他性质：
①椭圆上到中心的距离最小的点是短轴的两个端点，到中心距离最大的点是长轴的两个端点．
②椭圆上到焦点距离最大、最小的点是长轴的两个端点，最大距离是，最小距离是．
③设椭圆的两个焦点为，，是椭圆上的点，当点在短轴的端点时最大．
④椭圆的焦点的光学性质：从任一焦点发出的光线通过椭圆面反射后，反射光线经过另一焦点．
2. 椭圆中的相关结论：
①若在椭圆上，则过的椭圆的切线方程是；
②若在椭圆外 ，则过作椭圆的两条切线切点为，则切点弦的直线方程是；
③椭圆 ()的左右焦点分别为，点为椭圆上任意一点，则椭圆的焦点角形的面积为；
④是椭圆的不平行于对称轴的弦，为的中点，则，即；
⑤已知椭圆，直线交椭圆于，两点，点是椭圆上异于，的任一点，且，均存在，则．
⑥过椭圆的右焦点作直线交轴于点，交椭圆于点和，若，，则．




知识点一：椭圆的方程及性质
知识梳理
椭圆定义：平面内到两个定点，（）的距离的和等于常数的点的轨迹叫做椭圆．这两个定点，叫做椭圆的焦点，两个焦点的距离叫做焦距．
注意：若设动点为，则
（1）当时，动点的轨迹是椭圆．
（2）当时，动点的轨迹是线段．
（3）当时，动点的轨迹不存在．




例题精讲
例1．（1）椭圆的短轴长为（ ）
A. B. C. D.
【答案】B
【详解】，短轴长为4
例2. （1）若方程表示焦点在轴上的椭圆，则实数的取值范围是（ ）
A． B． C． D．
【答案】C
【详解】 焦点在轴， ， .
例3.已知的顶点、，顶点在直线上移动，求重心的轨迹．
【答案】
【解析】设，两点的坐标分别为，则．由重心坐标公式，得由上式可得所以．化简得．
例4.已知、是两个定点，且，动点到定点的距离是4，线段的垂直平分线交线段于点，求动点的轨迹方程．

【答案】
【解析】过，两点的直线为轴，，两点的中点为坐标原点，建立直角坐标系
∵，∴，两点坐标分别为，．
连结．∵垂直平分线段，
∴，．
由椭圆的方程可得：，即为所求点轨迹方程．
例5.已知椭圆E：＋＝1（a＞b＞0）的右焦点为F（3,0），过点F的直线交E于A，B两点．若AB的中点坐标为（1，－1），则E的方程为（ ）
A． B．＝1 C．＝1 D．＝1
【答案】D
【详解】因为直线AB过点F（3,0）和点（1，－1），所以直线AB的方程为y＝（x－3），代入椭圆方程＋＝1消去y，得x2－a2x＋a2－a2b2＝0，所以AB的中点的横坐标为＝1，即a2＝2b2，又a2＝b2＋c2，所以b＝c＝3，a＝3，椭圆方程为．

例6.已知⊙Q：(x-1)2+y2=16,动⊙M过定点P(-1,0)且与⊙Q相切，则M点的轨迹方程是 。
【答案】

【解析】P(-1,0)在⊙Q内，故⊙M与⊙Q内切，记：M(x,y)，⊙M的半径是为r，则：
|MQ|=4-r，又⊙M过点P，∴|MP|=r，于是有：|MQ|=4-|MP|，即|MQ|+|MP|=4，可见M点的轨迹是以P、Q为焦点（c=1）的椭圆，a=2。

例7.已知焦点在轴上的椭圆F1,F2是它的两个焦点，若椭圆上存在点P，使得，则的取值范围是 。
【答案】(0,
【解析】
思路一：先证一个结论：若B为椭圆短轴端点，则∠F1PF2≤∠F1BF2。记∠F1PF2=,
|PF1|=r1, |PF2|=r2,cos===
又≤()2=,∴cos≥=cos∠F1BF2,当且仅当r1=r2时等号成立，[来源:Z.xx.k.Com]
即∠F1PF2≤∠F1BF2。题中椭圆上存在点P，使得∠F1PF2=900，当且仅当∠F1BF2≥900，即
cos∠F1BO≤b≤a=,∴b∈(0, .
思路二：用勾股定理：r1+r2=2a ①
r12+r22=4c2 ②,由①②得：2r1r2=4b2,又2r1r2≤r12+r22 ∴b2≤c2=4-b2 即b∈(0, .
思路三：用向量的坐标运算：记P(x0,y0),=(-c-x0,-y0), =(c-x0,-y0),
=c2-x02+y02=0(b2+4)x02=4(c2-b2),注意到：0≤x02≤4，∴0≤4(c2-b2)≤4(b2+4)
即0≤4-2b2≤b2+4，得b∈(0, .
巩固练习
1.点在椭圆上运动，、分别在两圆和上运动，则的最大值为 ，最小值为 ．
【答案】6，2
【解析】，，，
把点想成定点，，

又，∴；
类似，．
2.点到定点的距离和它到定直线的距离之比为，则的轨迹方程是（ ）
A． B． C． D．
【答案】C
【详解】设点为,由题意得,,即,,整理得到,故选：C

3.椭圆的右焦点为，点是椭圆上一动点，点是圆上一动点，
求的最大值及此时点的坐标．
【答案】，
【解析】利用椭圆定义进行转化

此时，
4.已知椭圆C：＋＝1，点M与C的焦点不重合．若M关于C的焦点的对称点分别为A，B，线段MN的中点在C上，则|AN|＋|BN|＝________．
【答案】12
【解析】椭圆＋＝1中，a＝3.
如图，设MN的中点为D，则|DF1|＋|DF2|＝2a＝6.
∵D，F1，F2分别为MN，AM，BM的中点，
∴|BN|＝2|DF2|，|AN|＝2|DF1|，∴|AN|＋|BN|＝2(|DF1|＋|DF2|)＝12.
5.若动点（）在曲线上变化，则的最大值为 （ ）
A． B．
C． D．2
【答案】A
【解析】本题可以直接借助于椭圆方程把x2用y表示，从而得到一个关于y 的二次函数，再配方求最值；这里用椭圆的参数方程求解：x=2cos,y=bsin,=4cos2+2bsin=f()，
f()=-4sin2+2bsin+4=-4(sin-)2+, sin∈[-1,1]
若0<≤101b>4,则当sin=1时f()取得最大值2，故选A




知识点二：直线与椭圆
知识梳理
1、直线与圆锥曲线的位置关系的判断：
（1）相交：直线与椭圆相交；
（2）相切：直线与椭圆相切；
（3）相离：直线与椭圆相离；

2、弦长公式：
若直线与圆锥曲线相交于两点A、B，且分别为A、B的横坐标，则＝，
若分别为A、B的纵坐标，则＝，
若弦AB所在直线方程设为，则＝。

例题精讲
1.点差法
例10.过椭圆内一点M（2，1）引一条弦，使弦被点M平分，求这条弦所在的直线
方程。

【答案】
【解析】设直线与椭圆的交点为A()，B（），M（2，1）为AB的中点，
所以，，
又A、B两点在椭圆上，则，，
两式相减得，
所以，即，
故所求直线方程为。
例11. 过椭圆上一点P（-8，0）作直线交椭圆于Q点，求PQ中点的轨迹方程。
【答案】
【解析】设弦PQ中点M（），弦端点P（），Q（），
则有，
两式相减得，
又因为，，所以，
所以，
而，故。
化简可得 （）。
2.弦长公式
例12. 已知椭圆及直线．
（1）当为何值时，直线与椭圆有公共点？
（2）若直线被椭圆截得的弦长为，求直线的方程．
分析：直线与椭圆有公共点，等价于它们的方程组成的方程组有解．因此，只须考虑方程组消元后所得的一元二次方程的根的判别式．已知弦长，由弦长公式就可求出．

【答案】(1)． (2)
【解析】（1）把直线方程代入椭圆方程得
，即．
， 解得．
（2）设直线与椭圆的两个交点的横坐标为，，由（1）得 ，．
根据弦长公式得 ． 解得．
因此，所求直线的方程为．


例13. 已知长轴为12，短轴长为6，焦点在轴上的椭圆，过它对的左焦点作倾斜解为的直线交椭圆于，两点，求弦的长．
分析：此类题目是求弦长问题，这种题目方法很多，可以利用弦长公式求得，也可以利用椭圆定义及余弦定理，还可以利用焦点半径来求．
【答案】
【解析】(法1)利用直线与椭圆相交的弦长公式求解．

．
因为，，所以．
又因为焦点在轴上，所以椭圆方程为，左焦点，从而直线方程为．
由直线方程与椭圆方程联立得 ．
设，为方程两根， 所以，，，
从而．
(法2)利用椭圆的定义及余弦定理求解．
由题意可知椭圆方程为，设，，则，．
在中，，即；
所以．同理在中，用余弦定理得，所以．
例14.已知椭圆，、是椭圆上的两点，线段的垂直
平分线与轴相交于点.证明：
【答案】设，则中点，得
得
即，的垂直平分线的斜率
的垂直平分线方程为
当时，
而，
例15.已知椭圆，试确定的值，使得在此椭圆上存在不同两点关于直线对称。
【答案】
【解析】设，的中点，
而相减得
即，
而在椭圆内部，则即。
巩固练习
1. 求椭圆斜率为3的弦的中点轨迹方程。
【答案】
【解析】设弦中点M（），弦端点P（），Q（），
则有，
两式相减得，
又因为，，所以，
所以，
而，故。 化简可得 。
2.已知中心在原点，左焦点为的椭圆的左顶点为，上顶点为，到直线的距离为.
(1) 求椭圆的方程；
(2) 过的直线交椭圆于、两点，交直线于点，若是、的等比中项，求直线的方程；
(3) 圆以椭圆的两焦点为直径，圆的任意一条切线交椭圆于两点、，试求弦长的取值范围.
【答案】(1) (2) (3)
【解析】(1)设椭圆方程为：（）所以直线方程为：
∴到直线距离为
又，解得：，故：椭圆方程为：.
(2) 当直线与轴重合时，，而，所以
故可设直线方程为：，代人椭圆的方程，得：，
即： ∴
记，， ∴，
∵，即，∴
∴，解得：，符合，所以
故直线的方程为，即：
(3) 椭圆的两焦点为、，所以圆的方程为：
①若切线垂直于轴，则其方程为：，易求得
②若切线不垂直于轴，可设其方程为： 所以
将代人椭圆方程，得：
∴（*）
记、两点的坐标分别为、
此时：，
∴
令，所以，
∴

综合①②,得：弦长的取值范围为。
知识点三：最值问题

例题精讲
例16.设，，……，≥是二次曲线上的点，且，，……构成了一个公差为的等差数列，其中心是坐标原点，证，若，当公差d变化时，求的最小值为 ．
【答案】
【解析】原点O到二次曲线上各点的最小距离为b，最大距离为a
且

在上递增的最小值为








例17.已知椭圆的中心在坐标原点，焦点在坐标轴上，且经过、、三点．（Ⅰ）求椭圆的方程：
（Ⅱ）若点D为椭圆上不同于、的任意一点，，当Δ内切圆的面积最大时，求Δ内心的坐标；
【答案】（Ⅰ）（Ⅱ）
【解析】（Ⅰ）设椭圆方程为，将、、代入椭圆E的方程，得
解得.∴椭圆的方程 ．
（Ⅱ），设Δ边上的高为
当点在椭圆的上顶点时，最大为，所以的最大值为．
设Δ的内切圆的半径为，因为Δ的周长为定值6．所以，
所以的最大值为．所以内切圆圆心的坐标为.
知识要点：









例18.已知椭圆的焦点F1(―3,0)、F2(3,0)且与直线x―y+9=0有公共点，求其中长轴最短的椭圆方程.
【答案】
【解析】解法1：设椭圆为=1与直线方程x―y+9=0联立并消去y得：
(2 a2― 9) x2 + 18 a2 x + 90 a2―a4= 0，
由题设△=(18 a2)2―4(2 a2―9) (90 a2―a4) ≥0
a4―54 a2 + 405 ≥0a2≥45或a2≤9.∵a2－9> 0, ∴a2≥45, 故amin=3，
得（2a）min=6,此时椭圆方程为.
解法2：设椭圆=1与直线x―y+9=0的公共点为M(acosα,)，
则acosα―+9=0有解.
∵=―9cos(α+)=，∴||1≥9a2≥45,
M
F2
x
F1 1
O
y

F
∴amin=3，得（2a）min=6,此时椭圆的方程.
解法3：先求得F1(―3，0)关于直线x―y+9=0的对称点F(―9,6)，设直线F1F2与椭圆的交点为M，则2a=|MF1|+|MF2| =|MF| +|MF2|≥|FF2|=6，于是(2a)min=6,易得a2=45,b2=36，
此时椭圆的方程为.
巩固练习
1.椭圆=上一点到两焦点的距离之积为m，求m取最大值时的P点的坐标．
【答案】m最大值为25，P点坐标为（0，±3）．
【解析】设椭圆的左右焦点为F1、F2，根据椭圆的定义，可得|PF1|+|PF2|=2a=10，
∵|PF1|•|PF2|≤[（|PF1|+|PF2|）]2=25，当且仅当|PF1|=|PF2|=5时，P到两焦点距离之积为m有最大值为25，∴当m取最大值时，P点位于短轴的顶点，其坐标为（0，±3）．

知识点四：综合应用

例题精讲
例19.已知椭圆的方程为，其焦点在轴上，点为椭圆上一点．
（1）求该椭圆的标准方程；
（2）设动点满足，其中、是椭圆上的点，直线与的斜率之积为，求证：为定值；
（3）在（2）的条件下探究：是否存在两个定点，使得为定值？
若存在，给出证明；若不存在，请说明理由．
【答案】（1）因为点为椭圆上一点，所以，
得， 椭圆方程为
（2）设，又，化简得
则，，
，所以
（定值）
（3）因为动点满足，即，
所以点的轨迹为焦点的椭圆．
　　存在点)、，使得（定值）

例20.已知椭圆：的两个焦点为，，若椭圆上存在点使得为钝角，则该椭圆的离心率的取值范围是（ ）
A. B. C. D.
【答案】B
【详解】如图，当动点在椭圆长轴端点处沿椭圆弧向短轴端点移动时，对两个焦点的张角逐渐增大，当且仅当点位于短轴端点时，张角达到最大.所以要使椭圆上存在点使得为钝角，根据椭圆的对称性可知，即，，即，所以又，所以选B.


例21.椭圆上一点关于原点的对称点为为其右焦点，若，设，且，则该椭圆离心率的最大值为（ ）
A.1 B. C. D.
【答案】B
【详解】因为关于原点对称，所以也在椭圆上，设左焦点为，则，又因为，所以，是直角三角形斜边的中点，所以,，所以，所以，，所以，故e的最大值为．

例22.若椭圆内有圆，该圆的切线与椭圆交于两点，
且满足（其中为坐标原点），则的最小值是 ．
【解析】【设圆的切线方程为，、
代入椭圆方程得到关于的一元二次方程：
由韦达定理，得因为，所以
所以所以 ①
因为是圆的切线，所以，即
代入①式，得，所以


.巩固练习
1．已知椭圆C:()的左右焦点分别为,如果C上存在一点Q,使,则椭圆的离心率的取值范围为( )
A． B． C． D．
【答案】D
【详解】当Q是椭圆上下顶点时最大，∴,∴，
∴，∵，∴，∴所求取值范围为.
2．已知椭圆E：＋＝1（a＞b＞0）的右焦点为F（3,0），过点F的直线交E于A，B两点．若AB的中点坐标为（1，－1），则E的方程为（ ）
A． B．＝1 C．＝1 D．＝1
【答案】D
【详解】因为直线AB过点F（3,0）和点（1，－1），所以直线AB的方程为y＝（x－3），代入椭圆方程＋＝1消去y，得x2－a2x＋a2－a2b2＝0，所以AB的中点的横坐标为＝1，即a2＝2b2，又a2＝b2＋c2，所以b＝c＝3，a＝3，椭圆方程为．
3．设点在椭圆的长轴上，点是椭圆上任意一点．当的模最小时，点恰好落在椭圆的右顶点，求实数的取值范围．
【答案】
【解析】设为椭圆上的动点，由于椭圆方程为，故．
因为，所以
推出．
依题意可知，当时，取得最小值．而，故有，解得．
又点在椭圆的长轴上，即． 故实数的取值范围是．
4．已知椭圆，（1）过椭圆的左焦点引椭圆的割线，求截得的弦的中点的轨迹方程；（2）求斜率为2的平行弦中点的轨迹方程．
【答案】（1）（椭圆内部分）； （2）（椭圆内部分）．







1.“”是“椭圆的焦距为4”的（ ）
A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件
【答案】A
【详解】由题意，椭圆可化为，当时，，解得，当时，，解得，
即当或时，椭圆的焦距为4，所以“”是“椭圆的焦距为4”的充分不必要条件.故选：A.

2.椭圆的四个顶点为、、、，若四边形的内切圆恰好过椭圆的焦点，则椭圆的离心率是（ ）
A． B． C． D．
【答案】C
【详解】设四边形的内切圆的半径为，又该圆经过焦点所以，且在直角三角形中， 所以故，化简可得 由 所以 则 由 所以 .



3.过点，且与椭圆有相同的焦点的椭圆方程是（ ）
A. B. C. D.
【答案】A
【详解】由题椭圆方程为，设与已知椭圆共焦点的椭圆方程为，将点代入有：，整理有，由于，所以，则所求椭圆标准方程为.

4.如图，把椭圆的长轴分成等份，过每个分点作轴的垂线交椭圆的上半部分于七个点，是椭圆的一个焦点，
则____________.
【答案】35.
由椭圆的方程知
∴故填35.
5.如图，设椭圆的左右焦点分别为F1、F2，过焦点F1的直线交椭圆于A、B两点，
若△ABF2的内切圆的面积为π，设A、B两点的坐标分别为A（x1，y1）、B（x2，y2），
则|y1﹣y2|值为　．
【答案】38
∵椭圆中，a2=16且b2=4，∴a=4，，
可得椭圆的焦点分别为F1（﹣3，0）、F2（ 3，0），
设△ABF2的内切圆半径为r，∵△ABF2的内切圆面积为S=πr2=π，∴r=4，
根据椭圆的定义，得|AB|+|AF2|+|BF2|=（|AF1|+|AF2|）+（|BF1|+|BF2|）=4a=16．
∴△ABF2的面积 又∵△ABF2的面积
（A、B在x轴的两侧）∴，解之得．
6.在平面直角坐标系中，点为椭圆：的下顶点，，在椭圆上，若四边形为平行四边形，为直线的倾斜角，若，则椭圆的离心率的取值范围为（ ）
A． B． C． D．
【答案】A
【详解】因为是平行四边形，因此且，故，代入椭圆方程可得，所以．因，所以即，
所以即，解得，故选A．

7.在△ABC中，已知A(2，0)，B(－2，0)，G，M为平面上的两点且满足GA+GB+GC=0,MA=MB=MC，GM//AB，则顶点C的轨迹为( )
A．焦点在x轴上的椭圆(长轴端点除外) B．焦点在y轴上的椭圆(短轴端点除外)
C．焦点在x轴上的双曲线(实轴端点除外) D．焦点在x轴上的抛物线(顶点除外)
【答案】B
【详解】设C(x，y)(y≠0)，因为GA+GB+GC=0，所以G为△ABC的重心，G(-2+2+x3,y3)，即G(x3,y3).又MA=MB=MC，即M为△ABC的外心，所以点M在y轴上，又GM//AB，则有M(0,y3).
又因为MB=MC，所以x2+(y-y3)2=4+y29，化简得x24+y212=1，y≠0.所以顶点C的轨迹为焦点在y轴上的椭圆(除去短轴端点)．故选B.

8. 已知椭圆，试确定的值，使得在此椭圆上存在不同两点关于直线对称。
【答案】.
设，的中点，
而相减得
即，
而在椭圆内部，则即。






9.已知点在以坐标轴为对称轴的椭圆上，点到两焦点的距离分别为和，过点作焦点所在轴的垂线，它恰好过椭圆的一个焦点，求椭圆方程．
分析：讨论椭圆方程的类型，根据题设求出和（或和）的值．从而求得椭圆方程．
【答案】设两焦点为、，且，．
从椭圆定义知．即．从知垂直焦点所在的对称轴，所以在中，，可求出，，从而．
∴所求椭圆方程为或．
10.在平面直角坐标系中，已知动点，点点与点关于直线对称，且．直线是过点的任意一条直线．
（1）求动点所在曲线的轨迹方程；
（2）设直线与曲线交于两点，且，求直线的方程；
（3）若直线与曲线交于两点，与线段交于点(点不同于点)，直线与直线交于点，求证：是定值．
【答案】（1）依据题意，可得点. ．　　　　　　　　　
又，. 所求动点的轨迹方程为.
（2）若直线轴，则可求得，这与已知矛盾，因此满足题意的直线不平行于轴．
设直线的斜率为，则．由 得．

设点，有 且恒成立（因点在椭圆内部）．
　又，于是，，即，解得．所以，所求直线． 　
证明（3）直线与线段交于点，且与点不重合，直线的斜率满足：．
由（2）可得点，可算得．
　 又直线．
　 设点，则由得（此等式右边为正数）.
，且=．
，解得. 为定值.



笔耕不辍

求椭圆方程的方法：除了根据定义外，常用待定系数法（先定形，后定式，再定量）.
当椭圆的焦点位置不明确而无法确定是哪种标准方程时，可设方程为（）
可以避免讨论和繁杂的计算，也可以设为（,）.
椭圆有“六点”（两个焦点，四个顶点），“两形”（中心，焦点以及短轴端点构成的三角形、椭圆上一点和两焦点构成的三角形）.要注意它们之间的位置关系（如焦点在长轴上等）及相互间的距离（如焦点到相应顶点的距离为）.
要重视椭圆定义解题的重要作用，要注意归纳提炼，优化解题过程，简化解题过程.

4．有关圆锥曲线弦的中点和斜率问题可利用“点差法”及结论：
设椭圆：上弦AB的中点为M(x0,y0),则斜率kAB=,
对椭圆：, 则kAB=．
5.用待定系数法求椭圆标准方程的一般步骤：
(1)作判断：根据条件判断焦点的位置．
(2)设方程：焦点不确定时，要注意分类讨论，或设方程为mx2＋ny2＝1(m>0，n>0，m≠n)．
(3)找关系：根据已知条件，建立关于a、b、c或m、n的方程组．
(4)求解，得方程．
(5)与椭圆＋＝1(a>b>0)共焦点的椭圆系方程为＋＝1(a>b>0，k＋b2>0)恰当运用椭圆系方程，可使运算简便．