第36讲-排列组合、概率-【高考培优直通车】2022年高三数学大一轮复习精品讲义（上海专用）

这是一份第36讲-排列组合、概率-【高考培优直通车】2022年高三数学大一轮复习精品讲义（上海专用），文件包含第36讲-排列组合概率解析版-高考培优直通车-2022年高三数学大一轮复习教案上海专用docx、第36讲-排列组合概率原卷版-高考培优直通车-2022年高三数学大一轮复习教案上海专用docx等2份试卷配套教学资源，其中试卷共36页， 欢迎下载使用。

第36讲-排列组合、概率（解析版）
学习目标：
1. 掌握排列组合的概念和公式；
2. 能够运用排列组合解决一些实际问题；
3. 熟练掌握概率的相关概念和计算方法.

教学内容

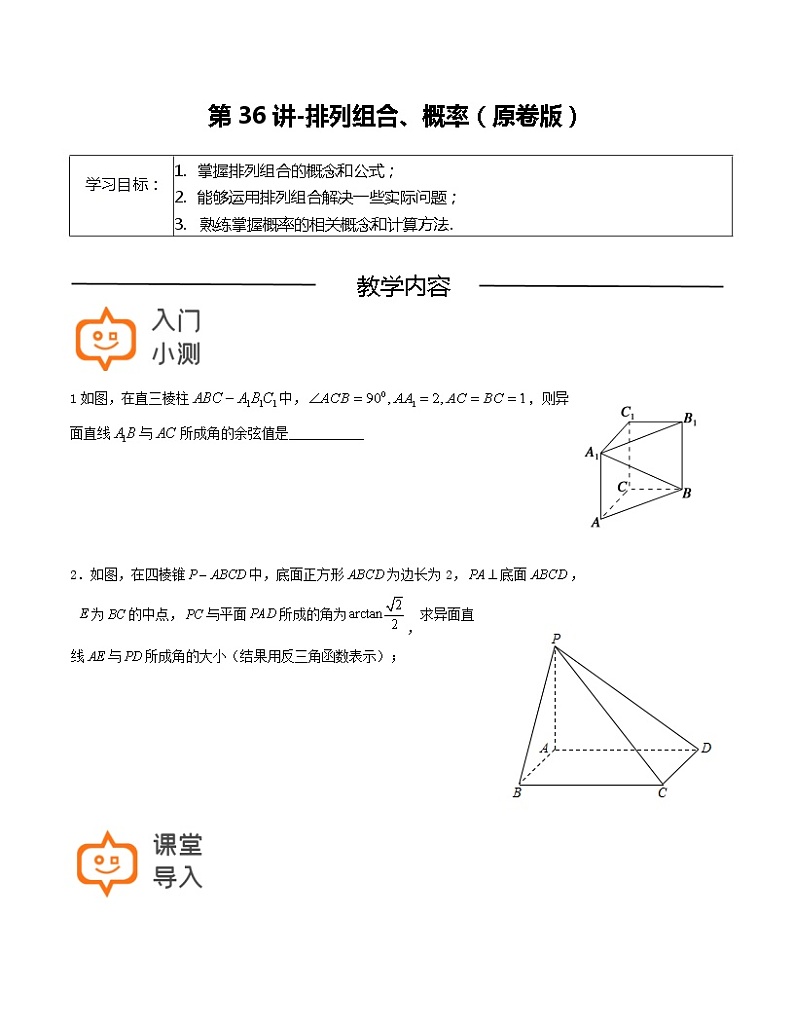
1如图，在直三棱柱中，，则异面直线与所成角的余弦值是___________
【答案】
【解析】

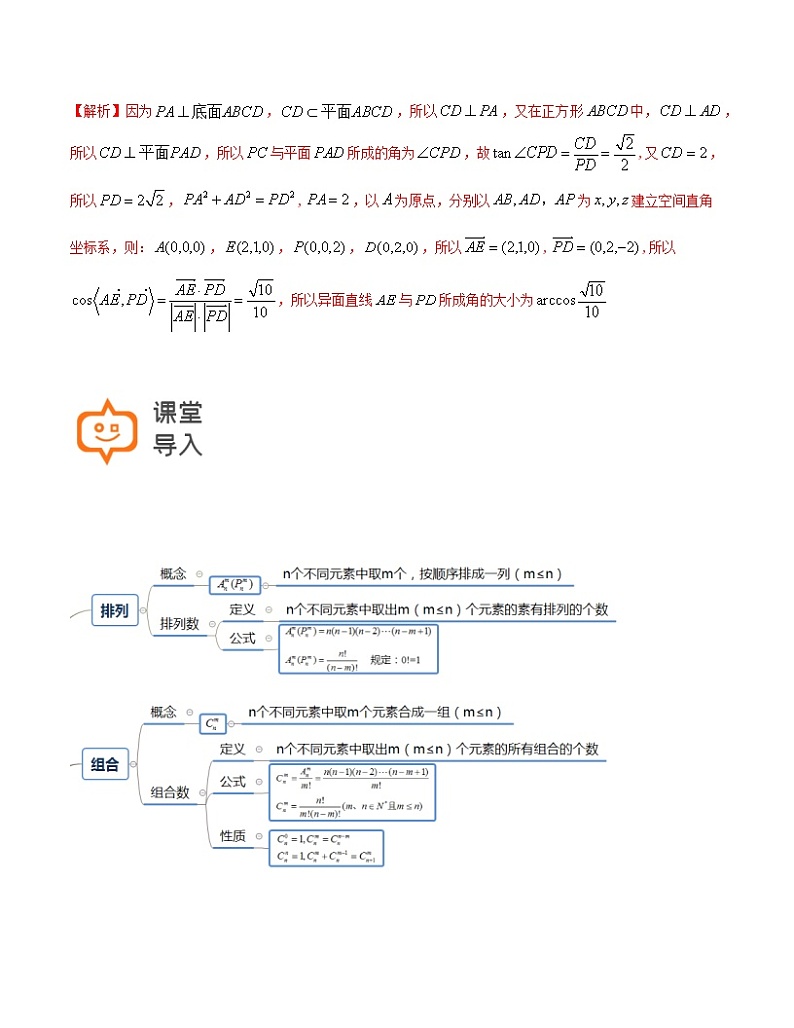
2．如图，在四棱锥中，底面正方形为边长为2，底面，
为的中点，与平面所成的角为，求异面直线与所成角的大小（结果用反三角函数表示）；


【答案】
【解析】因为，，所以，又在正方形中，，所以，所以与平面所成的角为，故,又，所以，,，以为原点，分别以为建立空间直角坐标系，则：，，，，所以,,所以，所以异面直线与所成角的大小为







知识点一（ 排列组合公式与性质 ）
（1） 排列数组合数

或（）

（2）全排列数：（叫做n的阶乘）规定．

（3）排列数的另一个计算公式：=

（4）组合数的性质1：


（5）组合数的性质2：＝+

【例题精讲】
例1 解方程或不等式：
（1）
【答案】
【解析】


（2） ；
【答案】
【解析】由题意得：，解得：且N*.
原方程化为，
即，
因为，所以，因此，即。
因为且，所以原方程的解为。

（3）
【答案】或或或
【解析】由题意得：且
原不等式化为，化简得：，即。
因为且，所以原不等式的解为或或或。
【巩固练习】
1 .解方程：．
【答案】
【解析】，
，
，
，或（负舍）。
2.满足的____．
【答案】
【解析】得，又，故

知识点二（区分排列组合重点掌握捆绑与插空法）
【知识梳理】
1、排列的定义：从个不同的元素中，任取个元素，按照一定的顺序排成一列，叫做从个不同元素中取出个元素的一个排列.
2、排列数：从个不同的元素中取出个元素的所有排列的个数，用符号表示
3、组合的定义：从个不同元素中，任取个元素，并成一组，叫做从个不同元素中取出个元素的一个组合.
4、组合数：从个不同的元素中取出个元素的所有组合的个数，用符号表示.

【例题精讲】
例1图书馆的书架上有种不同的报纸和种不同的杂志。
（1） 小明从该书架上任取一种刊物阅读，有多少种取法？

【答案】
【解析】分类计数原理：
（2）小明从该书架上各取一种刊物阅读，有多少种取法？
【答案】
【解析】分部计数原理：
例2 将封不同的信投入个不同的信箱，不同的投法共有（ ）
（A）种 （B）种 （C）种 （D）种
【答案】
【解析】每封信都有3个信箱来投
例3 的不同正约数共有多少个？
【答案】
【解析】将进行素因数分解，得：，
所以的不同正约数共有（个）。
例4 用组成正整数：
（1） 能组成多少个三位数；
【答案】
【解析】
（2） 能组成多少个无重复数字的三位数；
【答案】
【解析】或
（3） 能组成多少个三位奇数；
【答案】
【解析】
例5 现有 个女生和个男生排成一排，
（1） 如果女生必须排在一起，有多少种不同的排法？
【答案】
【解析】
（2） 如果女生必须排在一起，男生也必须排在一起，有多少种不同的排法？
【答案】
【解析】
（3） 如果女生必须分开，有多少种不同的排法？
【答案】
【解析】

（4） 如果女生必须分开，男生也必须分开，有多少种不同的排法？
【答案】
【解析】
（5） 如果两端都不能排女生，有多少种不同的排法？
【答案】
【解析】位置分析法：；元素分析法：
（6） 如果两端不能都排女生，有多少种不同的排法？
【答案】
【解析】 位置分析法：；元素分析法：
（7） 如果甲必须站在乙的左边（可以不相邻），有多少种不同的排法？
【答案】
【解析】定序问题用除法：
例6 现有个人站成一排：
1）甲不能站在排头，有多少种站法？
2）甲既不能站在排头，也不能站在排尾，有多少种站法？
3）甲不能站在排头，乙不能站在排尾，有多少种站法？
4）甲乙两人要站在相邻位置，有多少种站法？
5）甲乙两人不能相邻而站，有多少种站法？
【解析】
题号
从特殊元素入手考虑
从特殊位置入手考虑
间接法
1
甲有种选择：
排头从其余个人中选：


2
甲有种选择：
排头排尾从其余个人中选人排列：

3
甲站排尾有种；甲站中间位之一，乙除末位还有种选择：
甲不站排头的所有种数排除乙站排尾的情况：


4
甲紧邻乙左面的排法中先考虑甲，有种选法，且乙紧靠
甲，剩下位有种，再注意甲右乙左，故总数为
（捆绑法）将甲乙并为一个元素：

5
（插空法）除甲乙外人排好后，在这人的个间隙，排甲乙两人：
甲排排头，乙有种选择；甲排第位，乙有种选择；甲排第位，乙有种选择。由对称性得：



例7 从6名男医生和3名女医生中选出5人组成一个医疗小组。
（1）如果这个小组中男女医生都不能少于2人，共有多少种不同的建组方案？
（2）如果这个小组中必须男女医生都有，共有多少种不同的建组方案？

【答案】
【解析】（1）或；
思考典型错误：（错在哪里？）；
（2）或。
例8 有人去某地铁站参加志愿者活动，该地铁站有个出入口，要求每个出入口都要有志愿者服务，不同的安排方法有多少种？
【答案】
【解析】
例9某班位同学参加周一到周五的值日，每天安排一名学生，其中学生甲只能安排到周一或周二，学生乙不能安排在周五，则他们不同的值日安排有（ ）
A．种 B．种 C．种 D．种
【答案】D
【解析】甲有种安排，甲排好后，乙有种，然后剩下的人有种，共种
例10 现有位男生和位女生共位同学站成一排．若男生甲不站两端，位女生中有且只有两位女生相邻，则不同排法的种数为 （ ）
A． B． C．   D．
【答案】C
【解析】不妨将个位置从左到右编号为于是甲只能位于号位．
（1）当甲位于号位时，位女生必须分别位于位或者位．
于是相应的排法总数为；
（2）当甲位于号位时，位女生必须分别位于位或者位或者或者位．
于是相应的排法
（3）当甲位于号位时，情形与（1）相同．排法总数为．
综上，知本题所有的排法数为．
例11 马路上有盏灯，为了节约用电，可以熄灭其中盏灯，但两端的灯不能熄灭，
也不能熄灭相邻的两盏灯，那么熄灯方法共有______种．
【答案】
【解析】去掉两段的灯，中间有盏灯，在盏亮着的灯中有个空位，插入盏熄灭的灯即
例12某人连续射击次有四次命中，其中有三次连续命中，按“中”与“不中”报告结果，不同的结果有多少种．
【答案】
【解析】把问题转化为四个相同的黑球与四个相同白球，
其中只有三个黑球相邻的排列问题，将三黑球“捆绑”在一起看成一个“黑球”，与另一个黑球插入四个白球的空档中，共有种不同的结果．

【巩固练习】
1．下列等式中正确的是( )
(1)； (2)；
(3)； (4)．
A．(1)(2) B．(1)(2)(3)
C．(1)(3) D．(2)(3)(4)
【答案】B
【解析】根据组合公式进行化简

2.要将个不同的小球放入个不同的盒子，恰有个盒子空着，共有多少种不同的放置方式？
【答案】
【解析】
3.把名男生和名女生排成一排，女生要排在一起，不同的排法种数为____．
【答案】
【解析】捆绑法；

4．有本不同的书，其中数学书本，外文书本，其他书本，若将这些书连排成一列放在书架上，则数学书恰好排在一起，外文书也恰好排成一起的排法有 种排法。
【答案】
【解析】捆绑法；
5. 不同的五种商品在货架上排成一排，其中，两种商品必须排在一起，而，两种商品不排在一起, 则不同的排法共有多少种？
【答案】
【解析】，捆在一起与进行排列有；此时留下三个空，将,两种商品排进去一共有；最后将，“松绑”有．所以一共有＝种方法．

6.有五张卡片，它的正反面分别写，将它们任意三张并排放在一起组成三位数，共可组成多少个不同的三位数？
【答案】
【解析】此例正面求解需考虑卡片用与不用，且用此卡片又分使用与使用，
类别较复杂，因而可使用间接计算：任取三张卡片可以组成不同的三位数个，
其中0在百位的有个，这是不合题意的．
故共可组成不同的三位数-=432（个）

7．用这六个数字，可以组成无重复数字的四位偶数____个．
【答案】
【解析】主要采用特殊元素或特殊位置优先考虑的原则进行分类；当各位数字为0的时候共有个偶数，当各位数字不是0，个位数有2种选择，千位数有4种选择，故一共有个偶数，故共有个偶数满足条件。

8.用这七个数字组成没有重复数字的七位数中，
⑴若偶数次序一定，有多少个？
⑵若偶数次序一定，奇数的次序也一定的有多少个？
【答案】（1）；（2）
【解析】⑴；⑵

9.一个口袋内装有大小相同的个白球和个黑球．
⑴从口袋内取出个球，共有多少种取法？
⑵从口袋内取出个球，使其中含有个黑球，有多少种取法？
⑶从口袋内取出个球，使其中不含黑球，有多少种取法？
【答案】（1）；（2）；（3）
【解析】⑴从口袋内的个球中取出个球，取法种数是；
⑵从口袋内取出个球有个是黑球，于是还要从个白球中再取出个，
取法种数是；
⑶由于所取出的个球中不含黑球，也就是要从个白球中取出个球，
取法种数是．
知识点三（ 概率问题 ）
【知识梳理】
1.随机事件的概率
①试验
观察一定条件下发生的现象，通常叫做试验．事件的条件实现一次，称为一次试验．一个试验如果可以在相同的条件下重复进行，而且每次试验的结果可以不同，有偶然性，我们就称它为随机试验，简称试验．
②事件
基本事件：一次试验连同其中可能出现的每一具体结果称为一个基本事件，通常试验的某一事件A由几个基本事件组成．
随机事件：在一定条件下可能发生也可能不发生的事件．
必然事件：在一定条件下必然要发生的事件，记作．
不可能事件：在一定条件下不可能发生的事件，记作．
互斥事件：在同一次试验中，不可能同时发生的两个事件叫做互斥事件，也叫做互不相容事件．
对立事件：在一次试验中，如果两个互斥事件必然有一个发生，那么这两个事件叫做对立事件的一个事件．即设E和F是两个随机事件，满足（1）；（2）．
在任何一次试验中，如果把事件不出现记作事件，那么事件A与事件互为对立事件．
独立事件：如果事件出现和事件出现，互相之间没有影响，即其中一个事件的发生对另一事件发生的概率没有影响，那么就称事件和事件互相独立．
如果与是独立的，则与、与、与也是互相独立的．
【古典概率模型】
（1）一次试所有的基本事件只有有限个；
（2）每个基本事件出现的可能性相等，这样两个特点的概率模型叫做古典概率型．


2.古典概率模型

3.和事件
（1）和事件：设与为两个随机事件，把“事件与事件至少有一个出现”叫做事件与事件的和．
（2）和事件的概率（概率加法公式）：．



（3）互斥事件和的概率：如果事件与互斥，那么．
4.积事件
（1）积事件：设与为两个随机事件，把“与同时
出现”叫做与的积．
（2） 独立事件积的概率：如果事件与互相独立，那么．

总结：
关系
事件概率
含义
A、B互斥
A、B相互独立

与中至少有一个发生的概率



与都发生的概率
0


与都不发生的概率



与恰有一个发生的概率



与至多有一个发生的概率
1

【例题精讲】
1、 基本事件数的探求

例1做抛掷两颗骰子的试验：用表示结果，其中表示第一颗骰子出现的点数，表示第二颗骰子出现的点数，写出：
(1) 试验的基本事件；(2)事件“出现点数之和大于8”；
【答案】　(1)这个试验的基本事件为：
(1,1)，(1,2)，(1,3)，(1,4)，(1,5)，(1,6)
(2,1)，(2,2)，(2,3)，(2,4)，(2,5)，(2,6)
(3,1)，(3,2)，(3,3)，(3,4)，(3,5)，(3,6)
(4,1)，(4,2)，(4,3)，(4,4)，(4,5)，(4,6)
(5,1)，(5,2)，(5,3)，(5,4)，(5,5)，(5,6)
(6,1)，(6,2)，(6,3)，(6,4)，(6,5)，(6,6)
(2)事件“出现点数之和大于8”包含以下10个基本事件(3,6)，(4,5)，(4,6)(5,4)，(5,5)，(5,6)，(6,3)，(6,4)，(6,5)，(6,6)．

例2（1）向一个圆面内随机地投射一个点，如果该点落在圆内任意一点都是等可能的， 你认为这是古典概率吗?为什么？
（2）某同学随机地向一靶心进行射击，这一试验的结果只有有限个：命中10环. 命中9环……命中5环和不中环.你认为这是古典概率吗？为什么？
【答案】（1）不是古典概型，因为试验的所有可能结果是圆面内所有的点，试验的所有可能结果数是无限的，虽然每一个试验结果出现的“可能性相同”，但这个试验不满足古典概率的第一个条件.
（2）不是古典概率，因为试验的所有可能结果只有7个，而命中10环、命中9环……命中5环和不中环的出现不是等可能的，即不满足古典概率的第二个条件.

【巩固训练】
1.给出下列四个命题：
①“当时，”是必然事件；②“当时，”是不可能事件；③“当时，”是随机事件；④“当时，”是必然事件；其中正确的命题个数是：
A.0 B.1 C. 2 D.3
【答案】B

2.已知非空集合满足，给出以下四个命题：
①若任取，则是必然事件 ②若，则是不可能事件
③若任取，则是随机事件 ④若，则是必然事件
其中正确的个数是( )
A.1 B.2 C.3 D.4
【答案】C
【解析】①③④正确，②错误.

2、随机事件的概率
例3一个罐子里有同样大小、同样重量的20个玻璃球，其中4个是红色的，6个是黑色的，10个是无色的，经过充分混合后，从罐子中任意取出一球，求下列事件的概率：
（1）取到有色玻璃球；（2）取到红色玻璃球；（3）取到无色玻璃球；
【答案】（1）；（2）；（3）
【解析】（1）设某一个球被取到是一个基本事件.根据已知条件知，共有20个基本事件，每个基本事件的概率相等（为），20个玻璃球中有色玻璃球10个.如果把“取到有色玻璃球”的事件记作，那么
（2）20个玻璃球中有4个是红色的.如果把“取到红色玻璃球”的事件记作，那么
（3）如果把“取到无色玻璃球”的事件记作，那么 .

例4 某人有5把钥匙，但忘记了开房门的是哪一把，于是，他逐把不重复地试开，问：
（1）恰好第三次打开房门所的概率是多少？
（2）三次内打开的概率是多少？
（3）如果5把内有2把房门钥匙，那么三次内打开的概率是多少？
【答案】（1）；（2）；（3）。
【解析】 5把钥匙，逐把试开有种结果，由于该人忘记了开房间的是哪一把，因此这些结果是等可能的。
(1)第三次打开房门的结果有种，故第三次打开房门锁的概率；
(2)三次内打开房门的结果有种，因此所求概率；
(3)方法1 因5把内有2把房门钥匙，故三次内打不开的结果有种，从而三次内打开的结果有种，所求概率.
方法2 三次内打开的结果包括：三次内恰有一次打开的结果种；三次内恰有两次打开的结果种.因此，三次内打开的结果有（）种，所求概率.
【巩固训练】

1.从4名男生和2名女生中任选3人参加演讲比赛．
(1) 求所选3人都是男生的概率；
(2) 求所选3人中恰有1名女生的概率；
(3) 求所选3人中至少有1名女生的概率，
【答案】(1) (2) (3)
【解析】（1）所选3人都是男生的概率为；
（2）所选3人中恰有1名女生的概率为；
（3）所选3人中至少有1名女生的概率为.

3、 互斥事件、对立事件的概率
例5 现有8名2012年伦敦奥运会志愿者，其中志愿者通晓日语，通晓俄语，通晓韩语．从中选出通晓日语、俄语和韩语的志愿者各1名，组成一个小组．
（1）求被选中的概率；
（2）求和不全被选中的概率．
【答案】（1）；（2）
【解析】（1）从8人中选出日语、俄语和韩语志愿者各1名，其一切可能的结果组成的基本事件共有个．由于每一个基本事件被抽取的机会均等，因此这些基本事件的发生是等可能的．
用表示“恰被选中”这一事件，事件由，因而.
（2）用表示“不全被选中”这一事件，则其对立事件表示“全被选中”这一事件，由于包含3个结果，事件有3个基本事件组成，所以，由对立事件的概率公式得.

例6有三种产品，合格率分别是0.90，0.95和0.95，各抽取一件进行检验.
（1）求恰有一件不合格的概率；（2）求至少有两件不合格的概率.（精确到0.001）
【答案】（1）0.176；（2）0.012
【解析】本题要主考查相互独立事件概率的计算，运用数学知识解决问题的能力,正确利用相互独立事件、互斥事件、独立事件重复发生概率的计算公式解决此类问题.
设三种产品各抽取一件，抽到合格产品的事件分别为A、B和C.
（1），
因为事件A，B，C相互独立，恰有一件不合格的概率为

答：恰有一件不合格的概率为0.176.
(2)方法1 至少有两件不合格的概率为

方法2 三件产品都合格的概率为
由（1）知，恰有一件不合格的概率为0.176，所以至有两件不合格的概率为

答：至少有两件不合的概率为0.012.

【巩固训练】
1.甲、乙、丙三位同学上课后独立完成5道自我检测题，甲及格概率为，乙及格概率为，丙及格概率为，则三人中至少有一人及格的概率为（ ）
　A．　　　　B．　　　　　 C．　　　　　　D．
【答案】B
【解析】先求出甲乙丙三位同学不及格的概率，三人中至少有一人及格的对立事件为三个人都不及格。
设甲及格为时间A，乙及格为事件B，丙及格为事件C,

2.一台机床有的时间加工零件A, 其余时间加工零件B, 加工A时,停机的概率是,加工B时,停机的概率是, 则这台机床停机的概率为（ ）
A. B. C. D.
【答案】A
【解析】机床停机的概率就是两种零件都不能加工的概率，即.

3.盒中有6只灯泡，其中2只次品，4只正品，有放回地从中任取两次，每次取一只，试求下列事件的概率：
（1）取到的2只都是次品；
（2）取到的2只中正品、次品各一只；
（3）取到的2只中至少有一只正品。
【答案】（1）；（2）；（3）
【解析】从6只灯泡中有放回地任取两只，共有,种不同取法，
（1）取到的2只都是次品情况为种，因而所求概率为；　　　　　
（2）由于取到的2只中正品、次品各一只有两种可能：第一次取到正品，第二次取到次品；及第一次取到次品，第二次取到正品。因而所求概率为；
（3）由于“取到的两只中至少有一只正品”是事件“取到的两只都是次品”的对立事件，因而所求概率为.

4.有朋自远方来，已知他乘火车、轮船、汽车、飞机来的概率分别是0.3，0.2，0.1，0.4．
（1）求他乘火车或飞机来的概率；
（2）求他不乘轮船来的概率；
（3）如果他来的概率为0.4，请问他有可能是乘何种交通工具来的？
【答案】（1）0.7；（2）0.8；（3）可能是乘飞机来，也可能是乘火车或汽车来的
【解析】设“朋友乘火车、轮船、汽车、飞机来”分别为事件，则，且事件之间是互斥的．
（1）他乘火车或飞机来的概率为.
（2）他乘轮船来的概率是，所以他不乘轮船来的概率为．
（3）由于，所以他可能是乘飞机来，也可能是乘火车或汽车来的．







1解方程（1）
（2）
【答案】（1）4；（2）14
【解析】（1），
，
，
，或（舍）。
（2）两边同时乘以可得
解得（舍）

2．从集合{0，1，2，3，5，7，11}中任取3个元素分别作为直线方程中的，所得的经过坐标原点的直线有______条．(结果用数值表示)
【答案】30
【解析】任取的3个元素应不同，并且
只能从非零元素选取，所以
3.从5位同学中选派4位同学在周五、周六、周日参加公益活动，每人一天，要求周五有2人参加，周六、周日各1人参加，则不同的选派方法种数为（用数字作答） .
【答案】60
【解析】

4.某个停车场有12个停车位，今有8辆不同牌照的汽车需要停放，要使4个空位连在一起，则有_________种不同的停放方法.
【答案】362880
【解析】先排8辆汽车，共有种，而8辆汽车之间共有9个位置，插入4个空汽车位，故共有种。

5．已知，那么 （ ）
A． B． C． D．
【答案】C
【解析】根据概率的积的公式

6.某电脑用户计划用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘，根据需要，软件至少买3片，磁盘至少买2盒，则不同的选购方式有 ( )
A．5种 B．6种 C．7种 D．8种
【答案】C
【解析】由于本题种数不多，软件至少买3片，磁盘至少买2盒 分类加法共7种

7.有两排座位，前排11个座位，后排12个座位，现安排2人就座，规定前排中间的3个座位不能坐，并且这2人不左右相邻，那么不同排法的种数是 ( )
A．234种 B．346种 C．350种 D．363种
【答案】B
【解析】(1)前排中间的3个座位不能坐，并且这2个人不左右相邻，前排一个，后排一个共有(2)后排坐两个（不相邻）（3）前排左两个44个

8.三个女生和五个男生排成一排
⑴ 如果女生必须全排在一起，可有多少种不同的排法？
⑵ 如果女生必须全分开，可有多少种不同的排法？
⑶ 如果两端都不能排女生，可有多少种不同的排法？
【答案】（1）4320（2）14400（3）14400
【解析】⑴ （捆绑法）因为三个女生必须排在一起，所以可以先把她们看成一个整体，
这样同五个男生合一起共有六个元素，然成一排有种不同排法．对于其中的每一种排法，三个女生之间又都有种不同的排法，因此共有种不同的排法．
⑵ （插空法）要保证女生全分开，可先把五个男生排好，每两个相邻的男生之间留出一个空档．这样共有个空档，加上两边两个男生外侧的两个位置，共有六个位置，再把三个女生插入这六个位置中，只要保证每个位置至多插入一个女生，就能保证任间两个女生都不相邻．由于五个男生排成一排有种不同排法，对于其中任意一种排法，从上述六个位置中选出三个来让三个女生插入都有种方法，因此共有种不同的排法．
⑶ （间接法）个女生和个男生排成一排共有种不同的排法，从中扣除女生排在首位的种排法和女生排在末位的种排法，但这样两端都是女生的排法在扣除女生排在首位的情况时被扣去一次，在扣除女生排末位的情况时又被扣去一次，所以还需加一次回来，由于两端都是女生有种不同的排法，所以共有种不同的排法．

9．口袋中有质地、大小完全相同的5个球，编号分别为1，2，3，4，5，甲、乙两人玩一种游戏：甲先摸出一个球，记下编号，放回后乙再摸一个球，记下编号，如果两个编号的和为偶数算甲赢，否则算乙赢．
（1）甲、乙按以上规则各摸一个球，求事件“甲赢且编号的和为6”发生的概率；
（2）这种游戏规则公平吗?试说明理由．
【答案】（1）；（2）不公平
【解析】（1）设“甲胜且两数字之和为6”为事件，事件包含的基本事件为（1，5）,（2，4）（3，3）,（4，2）,（5，1），共5个．又甲、乙二人取出的数字共有5×5＝25（个）等可能的结果，所以．
（2） 这种游戏规则不公平． 设“甲胜”为事件，“乙胜”为事件，则甲胜即两数字之和为偶数所包含的基本事件数为13个：（1，1），（1，3），（1，5），（2，2），（2，4），（3，1），（3，3），（3，5），（4，2） ，（4，4），（5，1） ，（5，3），（5，5）．所以甲胜的概率，从而乙胜的概率,由于，所以这种游戏规则不公平．