第11讲 函数的图象-【高考艺术生专用】2022年高考数学一轮复习特训特练（基础版，全国通用版）

这是一份第11讲 函数的图象-【高考艺术生专用】2022年高考数学一轮复习特训特练（基础版，全国通用版），文件包含第11讲函数的图象-高考艺术生专用2022年高考数学一轮复习特训特练解析版基础版全国通用版docx、第11讲函数的图象-高考艺术生专用2022年高考数学一轮复习特训特练原卷版基础版全国通用版docx等2份试卷配套教学资源，其中试卷共15页， 欢迎下载使用。
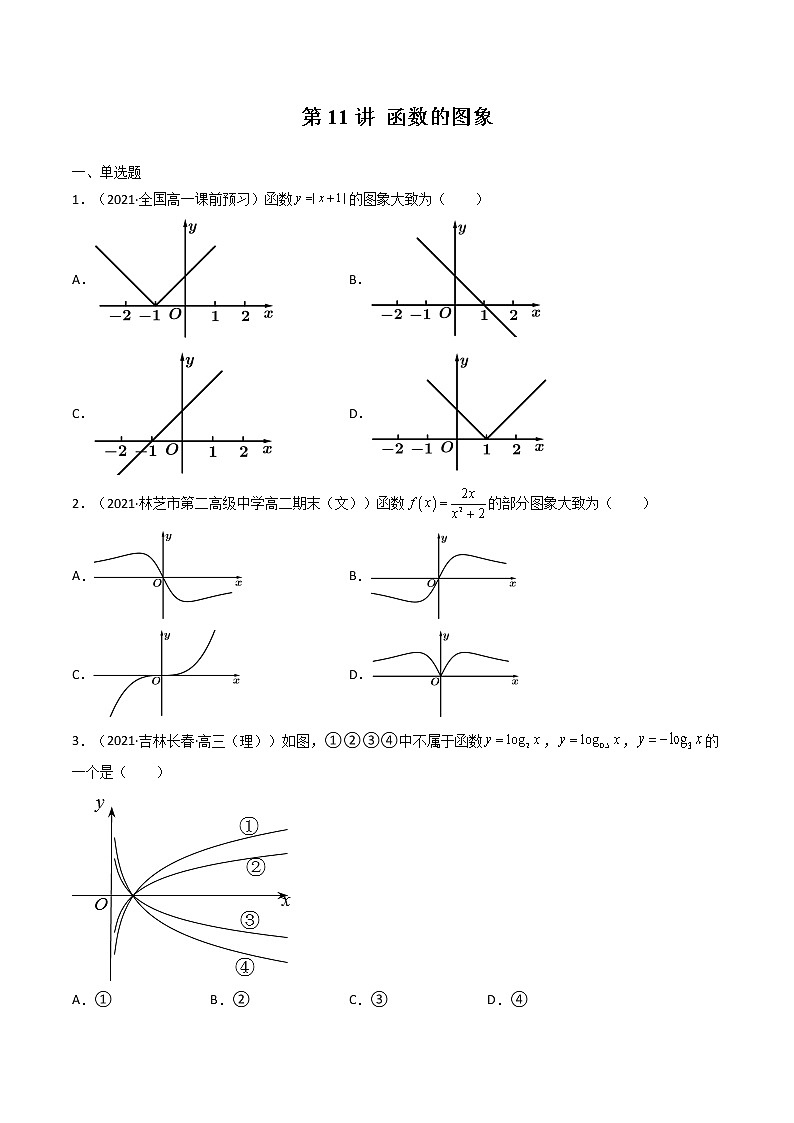
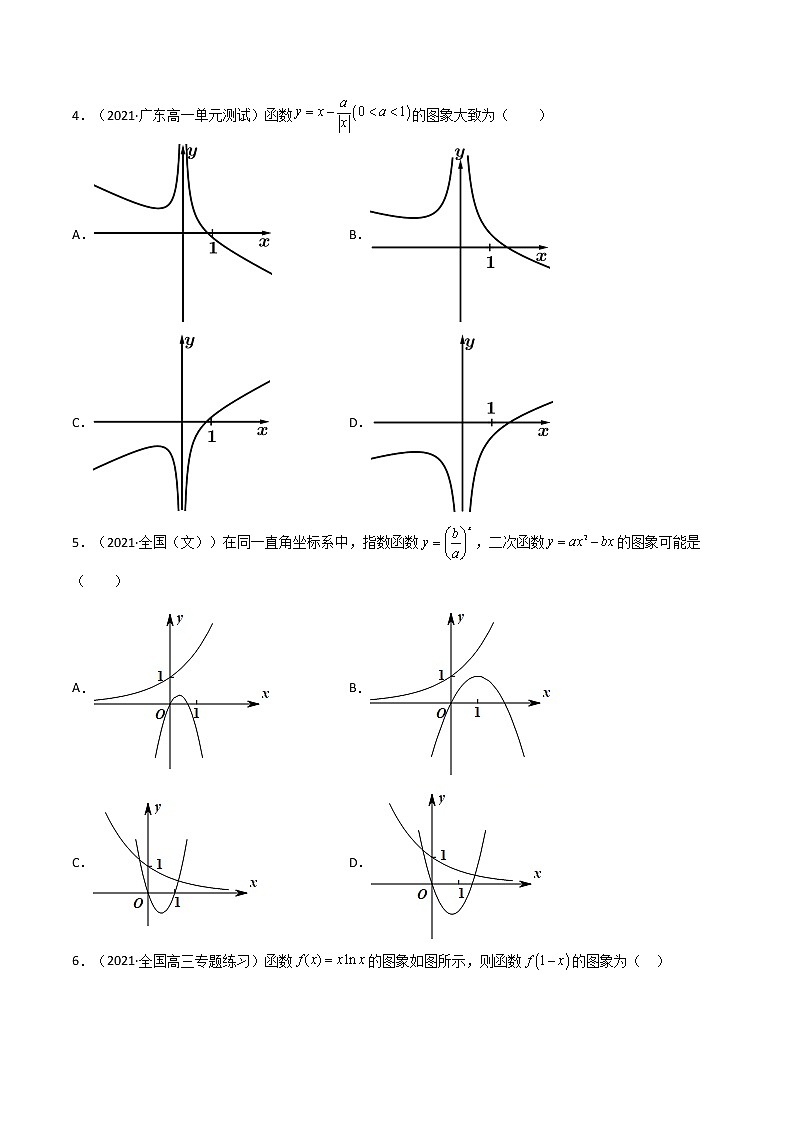
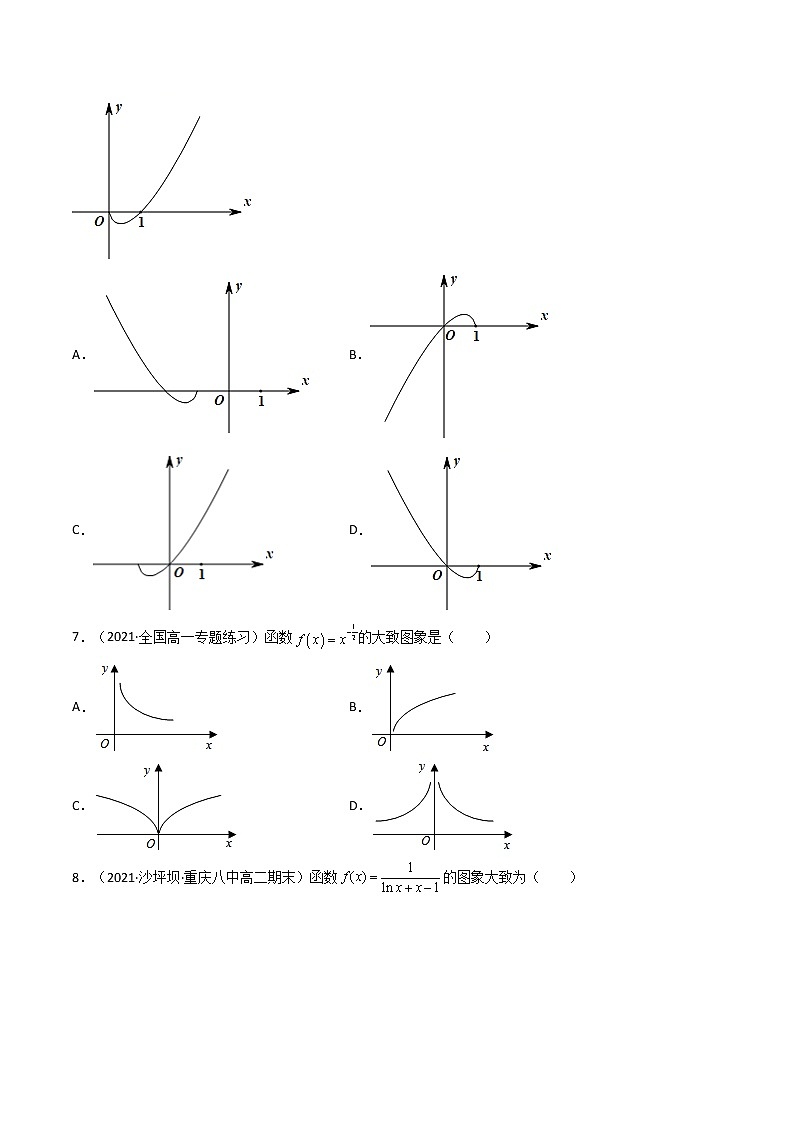
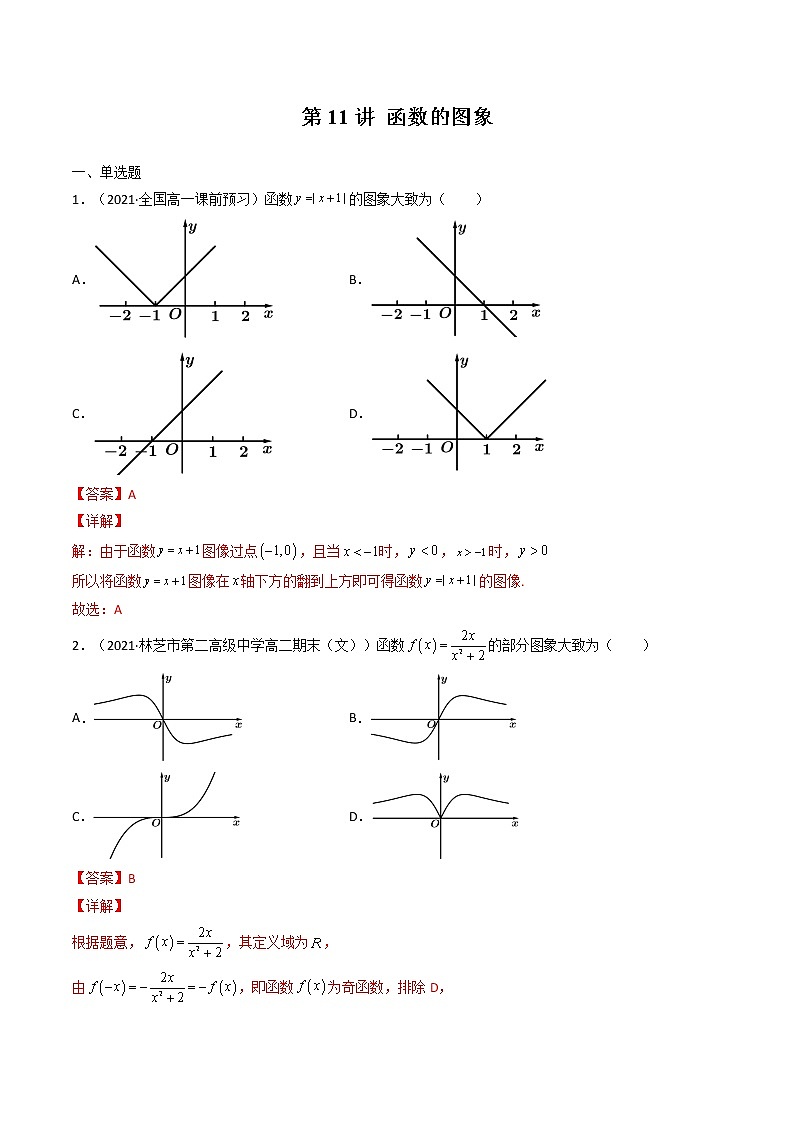
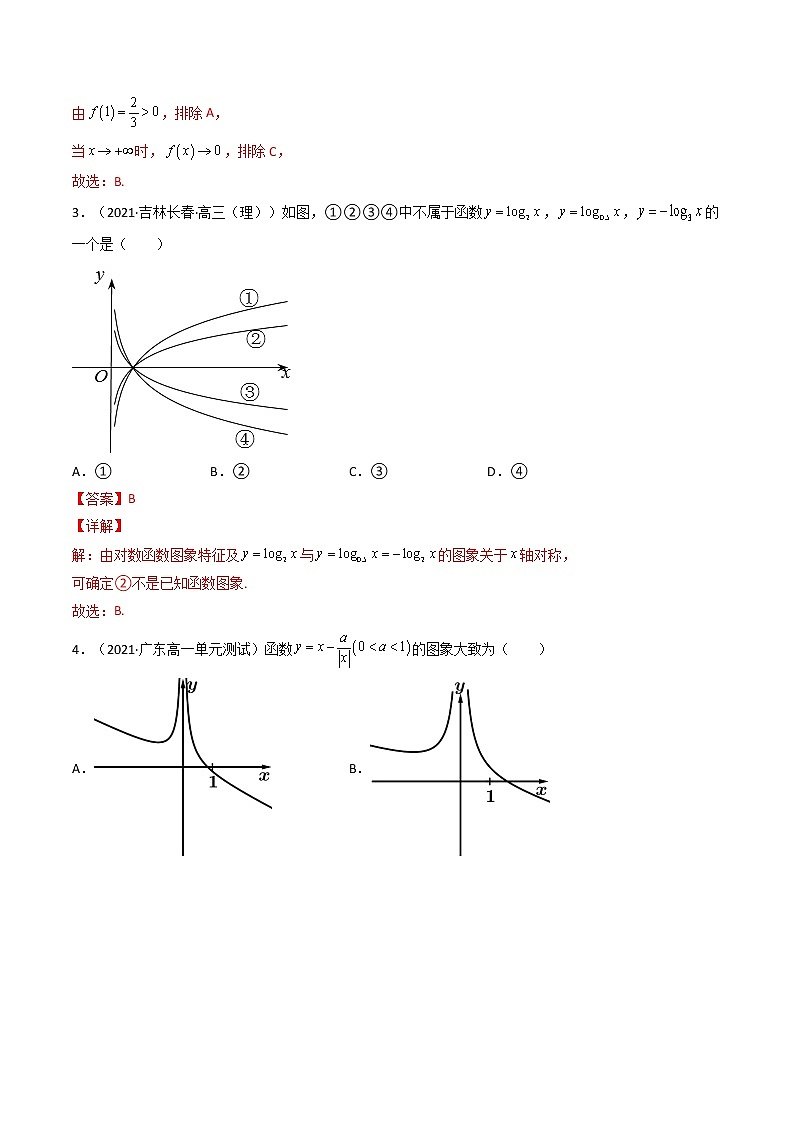
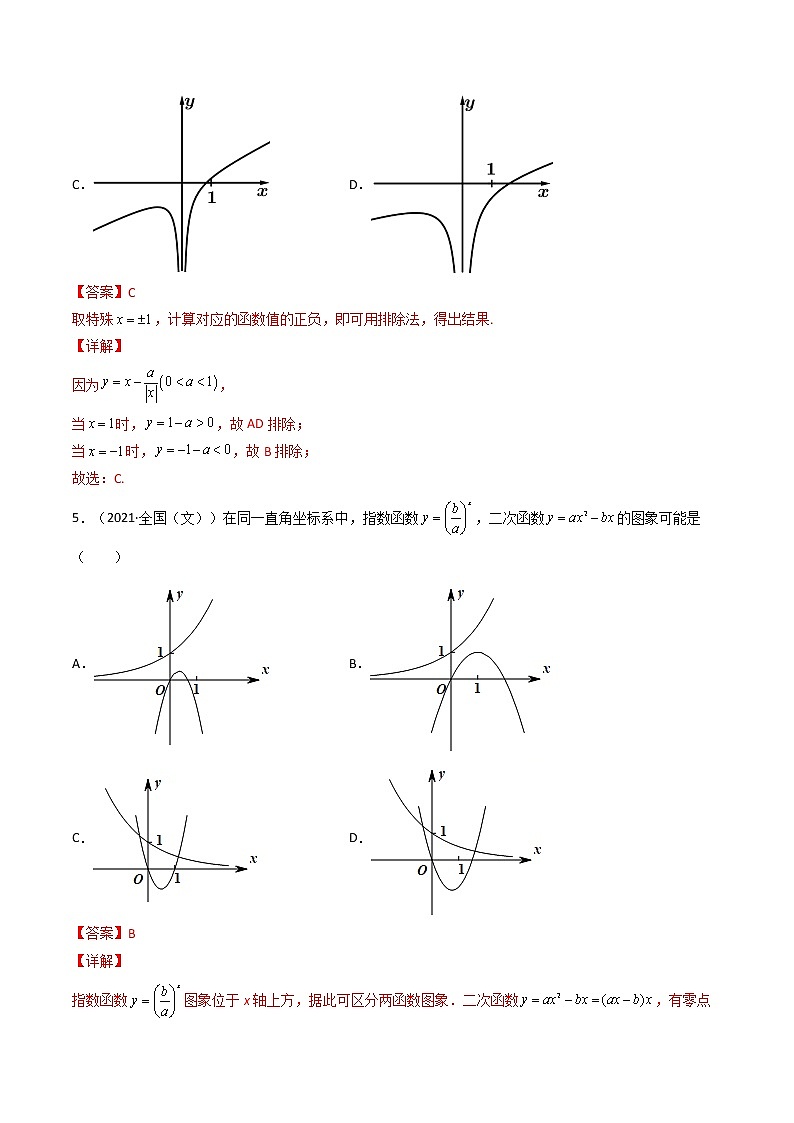
第11讲 函数的图象 一、单选题1．（2021·全国高一课前预习）函数的图象大致为（    ）A． B．C． D．【答案】A【详解】解：由于函数图像过点，且当时，，时，所以将函数图像在轴下方的翻到上方即可得函数的图像.故选：A2．（2021·林芝市第二高级中学高二期末（文））函数的部分图象大致为（    ）A． B． C． D．【答案】B【详解】根据题意，，其定义域为，由，即函数为奇函数，排除D，由，排除A，当时，，排除C，故选：B.3．（2021·吉林长春·高三（理））如图，①②③④中不属于函数，，的一个是（    ）A．① B．② C．③ D．④【答案】B【详解】解：由对数函数图象特征及与的图象关于轴对称，可确定②不是已知函数图象.故选：B.4．（2021·广东高一单元测试）函数的图象大致为（    ）A． B．C． D．【答案】C取特殊，计算对应的函数值的正负，即可用排除法，得出结果.【详解】因为，当时，，故AD排除；当时，，故B排除；故选：C.5．（2021·全国（文））在同一直角坐标系中，指数函数，二次函数的图象可能是（    ）A． B．C． D．【答案】B【详解】指数函数图象位于x轴上方，据此可区分两函数图象．二次函数，有零点．A，B选项中，指数函数在R上单调递增，故，故A错误、B正确．C，D选项中，指数函数在R上单调递减，故，故C，D错误．故选：B6．（2021·全国高三专题练习）函数的图象如图所示，则函数的图象为（  ）A． B．C． D．【答案】D【详解】将函数的图象作以轴为对称轴的翻折变换，得到函数的图象，再将图象向右平移一个单位，即可得到函数的图象．故选：D．7．（2021·全国高一专题练习）函数的大致图象是（    ）A． B．C． D．【答案】A【详解】由题意得，，所以函数的定义域为，因为，根据幂函数的性质，可知函数在第一象限为单调递减函数，故选：A．8．（2021·沙坪坝·重庆八中高二期末）函数的图象大致为（    ）A． B．C． D．【答案】B【详解】时，，可排除D；时，，可排除AC.故选：B.9．（2021·广东惠州·）已知的图象经过点，则的图象大致为（    ）．A． B．C． D．【答案】B【详解】因为经过，所以，所以，所以幂函数为，显然为奇函数，排除A、C：又因为在时，增长趋势比快速，所以排除D.故选：B．10．（2021·镇雄县第四中学）我国著名数学家华罗庚先生曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休”在数学的学习和研究中，常用函数的图象来研究函数的性质，也常用函数的解析式来琢函数的图象的特征，如函数的图象的是（    ）A． B．C． D．【答案】B【详解】，因此，函数的图象如B选项中的图象.故选：B.11．（2021·全国高一课时练习）函数与在同一坐标系中的图象大致是图中的（    ）A． B．C． D．【答案】A【详解】当时，在x，y轴上截距分别是，而开口向上，顶点为原点且对称轴为y轴，排除B；当时，在x，y轴上截距分别是，而开口向下，顶点为原点且对称轴为y轴，排除C、D；故选：A12．（2021·寿县第一中学）已知函数对任意的有，且当时，，则函数的图象大致为（    ）A． B．C． D．【答案】D【详解】由得，则函数是奇函数，排除A、C当时，，对应的图象为D，故选：D.二、填空题13．（2019·江苏南京市·）函数的图象向左平移个单位后所得新函数的图象恒过定点________.【答案】【详解】解：因为函数的图像向左平移个单位后所得新函数，又过定点，故答案为.14．（2019·瓦房店市实验高级中学高一月考）已知函数的图象如图所示，则不等式的解集为______．【答案】【详解】解：不等式等价为或，
则，或，
故不等式的解集是．
故答案为．15．（2018·全国）函数y＝3x2－x＋2的图象向左平移1个单位长度，再向下平移2个单位长度，所得图象对应的函数解析式是________________．【答案】y＝3x2＋5x＋2【详解】将函数y＝3x2－x＋2的图像向左平移1个单位长度，得y=3（x+1）-（x+1）+2=3x+5x+4，再向下平移2个单位长度，得y=3x+5x+2.故答案为y=3x+5x+216．（2015·四川眉山市·高一期中）函数的图象恒过点_______．【答案】【解析】试题分析：根据，当时，，所以函数恒过点