2020-2021学年江西省上饶四中七年级（下）期中数学试卷

这是一份2020-2021学年江西省上饶四中七年级（下）期中数学试卷，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2020-2021学年江西省上饶四中七年级（下）期中数学试卷
一、选择题（每小题3分，共18分）
1．（3分）在平面直角坐标系中，点P（﹣3，2）在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
2．（3分）如图，给出下列条件，①∠1＝∠3；②∠2＝∠4；③∠B＝∠DCE；④∠D＝∠DCE．其中能推出AD∥BC的条件为（　　）

A．②③④ B．②④ C．②③ D．①④
3．（3分）在实数，，，0.1010010001，，中，无理数有（　　）个．
A．1 B．2 C．3 D．4
4．（3分）由方程组可得出x与y的关系是（　　）
A．2x+y＝4 B．2x﹣y＝4 C．2x+y＝﹣4 D．2x﹣y＝﹣4
5．（3分）下列说法正确的是（　　）
A．一个数的算术平方根一定是正数
B．在同一平面内，过一点有且只有一条直线与已知直线垂直
C． 的立方根是4
D．在同一平面内，过一点有且只有一条直线与已知直线平行
6．（3分）已知点E（x0，y0），F（x2，y2），点M（x1，y1）是线段EF的中点，则x1，y1．在平面直角坐标系中有三个点A（1，﹣1），B（﹣1，﹣1），C（0，1），点P（0，2）关于A的对称点为P1（即P，A，P1三点共线，且PA＝P1A），P1关于B的对称点为P2，P2关于C的对称点为P3，按此规律继续以A，B，C为对称点重复前面的操作，依次得到P4，P5，P6，…，则点P2019的坐标是（　　）
A．（4，0） B．（﹣2，2） C．（2，﹣4） D．（﹣4，2）
二、填空题（每空3分，共18分）
7．（6分）若3，则a＝　 　．
8．（3分）命题“对顶角相等”的题设是　 　．
9．（3分）10.1，则±　 　．
10．（6分）如图三角形ABC平移后得到三角形DEF，若AE＝11，DB＝5，则平移的距离是 　 　．

11．（3分）如图，围棋盘放在某平面直角坐标系内，已知黑棋（甲）的坐标为（﹣2，1），黑棋（乙）的坐标为（﹣1，﹣2），则白棋（甲）的坐标是　 　．

12．（3分）一副直角三角尺叠放如图1所示，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动（旋转角不超过180度），使两块三角尺至少有一组边互相平行．如图2：当∠BAD＝15°时，BC∥DE．则∠BAD（0°＜∠BAD＜180°）其它所有可能符合条件的度数为 　 　．

三、解答题（共84分）
13．（6分）计算：
（1）﹣22|﹣5|；
（2）．
14．（6分）解方程或方程组
（1）4x2﹣16＝0；
（2）．
15．（6分）已知是m+3的算术平方根，，求的值．
16．（6分）如图，已知：AD⊥BC于D，EG⊥BC于G，∠E＝∠1．求证：AD平分∠BAC．

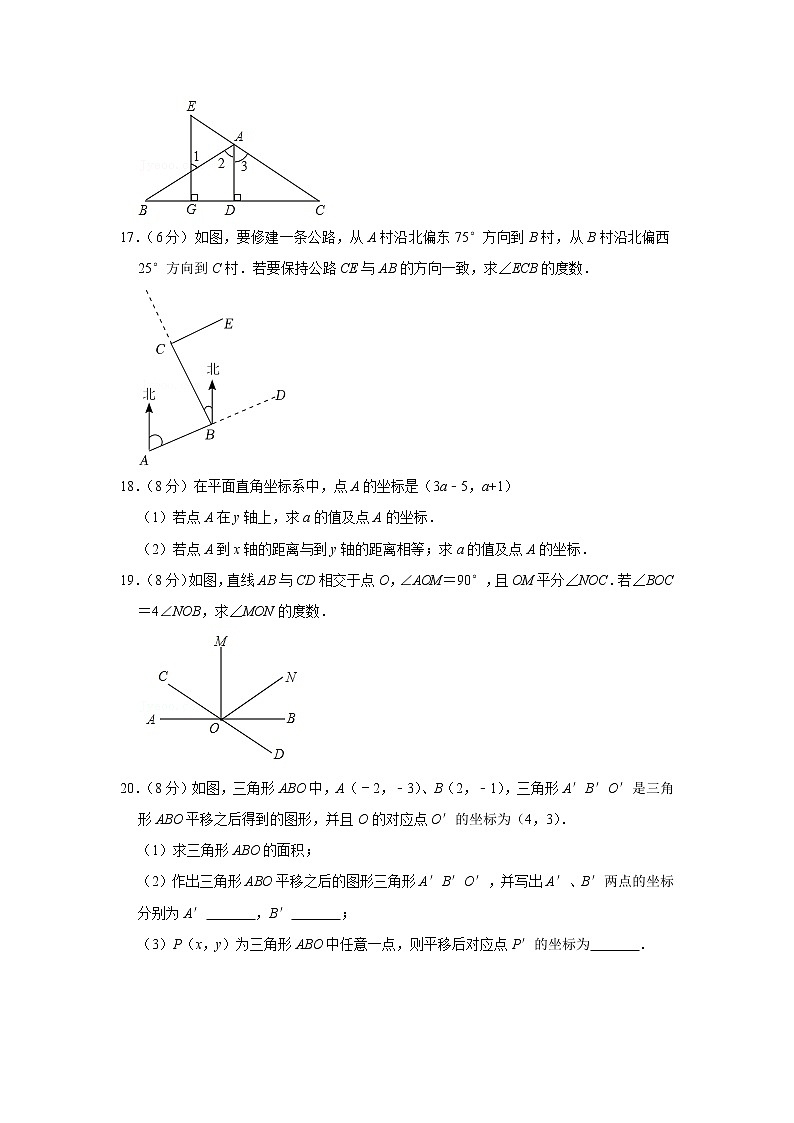
17．（6分）如图，要修建一条公路，从A村沿北偏东75°方向到B村，从B村沿北偏西25°方向到C村．若要保持公路CE与AB的方向一致，求∠ECB的度数．

18．（8分）在平面直角坐标系中，点A的坐标是（3a﹣5，a+1）
（1）若点A在y轴上，求a的值及点A的坐标．
（2）若点A到x轴的距离与到y轴的距离相等；求a的值及点A的坐标．
19．（8分）如图，直线AB与CD相交于点O，∠AOM＝90°，且OM平分∠NOC．若∠BOC＝4∠NOB，求∠MON的度数．

20．（8分）如图，三角形ABO中，A（﹣2，﹣3）、B（2，﹣1），三角形A′B′O′是三角形ABO平移之后得到的图形，并且O的对应点O′的坐标为（4，3）．
（1）求三角形ABO的面积；
（2）作出三角形ABO平移之后的图形三角形A′B′O′，并写出A′、B′两点的坐标分别为A′　 　，B′　 　；
（3）P（x，y）为三角形ABO中任意一点，则平移后对应点P′的坐标为　 　．

21．（8分）甲、乙两位同学在解方程组时，甲把字母a看错了得到方程组的解为；乙把字母b看错了得到方程组的解为．
（1）求a，b的正确值；
（2）求原方程组的解．
22．（10分）在平面直角坐标系xOy中，对于任意三点A，B，C的“矩面积”，给出如下定义：“水平底”d是任意两点横坐标差的最大值；“铅垂高”h是任意两点纵坐标差的最大值，则“矩面积”S＝dh．例如：A，B，C三点的坐标分别为（1，2），（﹣3，1），（2，﹣2），则“水平底”d＝5，“铅垂高”h＝4，“矩面积”S＝dh＝20．根据所给定义解决下面的问题：
（1）若点D，E，F的坐标分别为（﹣1，2），（2，﹣1），（0，6），求这三点的“矩面积”S；
（2）已知点D（﹣1，2），E（2，﹣2），在x轴上是否存在点F，使这三点的“矩面积”S为20？若存在，求出点F的坐标；若不存在，请说明理由．
23．（12分）材料1：反射定律
当入射光线MO照射到平面镜上时，将遵循平面镜反射定律，即反射角（∠NOH）的大小等于入射角（∠MOH）的大小，显然，这两个角的余角也相等，其中法线（OH）与平面镜（GF）垂直，并且满足入射光线（MO）、反射光线（ON）与法线在同一个平面．
材料2：平行逃逸角
对于某定角∠AOB＝α（0°＜α＜90°），点P为边OB上一点，从点P发出一光线PQ（射线），其角度为∠BPQ＝β（0°＜β＜90°），当光线PQ接触到边OA和OB时会遵循反射定律发生反射，当光线PQ经过n次反射后与边OA或OB平行时，称角β为定角α的n阶平行逃逸角，特别地，当光线PQ直接与OA平行时，称角β为定角α的零阶平行逃逸角．
（1）已知∠AOB＝α＝25°，
①如图1，若PQ∥OA，则∠BPQ＝　 　°，即该角为α的零阶平行逃逸角；
②如图2，经过一次反射后的光线P1Q∥OB，此时的∠BPP1为α的平行逃逸角，求∠BPP1的大小；
③若经过两次反射后的光线与OA平行，请补全图形，并求出α的二阶平行逃逸角；
（2）根据（1）的结论，归纳猜想对于任意角α（0°＜α＜90°），其n（n为自然数）阶平行逃逸角β＝　 　（用含n和α的代数式表示）．



2020-2021学年江西省上饶四中七年级（下）期中数学试卷
参考答案与试题解析
一、选择题（每小题3分，共18分）
1．（3分）在平面直角坐标系中，点P（﹣3，2）在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
【解答】解：点P（﹣3，2）在第二象限，
故选：B．
2．（3分）如图，给出下列条件，①∠1＝∠3；②∠2＝∠4；③∠B＝∠DCE；④∠D＝∠DCE．其中能推出AD∥BC的条件为（　　）

A．②③④ B．②④ C．②③ D．①④
【解答】解：①∵∠1＝∠3，
∴AB∥DC，本选项不符合题意；
②∵∠2＝∠4，∴AD∥CB，本选项符合题意；
③∵∠B＝∠DCE，
∴AB∥CD，本选项不符合题意；
④∵∠D＝∠DCE，
∴AD∥BC，本选项符合题意，
则符合题意的选项为②④．
故选：B．
3．（3分）在实数，，，0.1010010001，，中，无理数有（　　）个．
A．1 B．2 C．3 D．4
【解答】解：，0.1010010001是分数，属于有理数；
是整数，属于有理数；
无理数有，，，共3个．
故选：C．
4．（3分）由方程组可得出x与y的关系是（　　）
A．2x+y＝4 B．2x﹣y＝4 C．2x+y＝﹣4 D．2x﹣y＝﹣4
【解答】解：，
把②代入①得2x+y﹣3＝1，即2x+y＝4．
故选：A．
5．（3分）下列说法正确的是（　　）
A．一个数的算术平方根一定是正数
B．在同一平面内，过一点有且只有一条直线与已知直线垂直
C． 的立方根是4
D．在同一平面内，过一点有且只有一条直线与已知直线平行
【解答】解：A、一个数的算术平方根一定是正数和0，故本项错误；
B、在同一平面内，过一点有且只有一条直线与已知直线垂直，故本项正确；
C、8，的立方根是2，故本项错误；
D、在同一平面内，过直线外一点有且只有一条直线与已知直线平行，故本项错误．
故选：B．
6．（3分）已知点E（x0，y0），F（x2，y2），点M（x1，y1）是线段EF的中点，则x1，y1．在平面直角坐标系中有三个点A（1，﹣1），B（﹣1，﹣1），C（0，1），点P（0，2）关于A的对称点为P1（即P，A，P1三点共线，且PA＝P1A），P1关于B的对称点为P2，P2关于C的对称点为P3，按此规律继续以A，B，C为对称点重复前面的操作，依次得到P4，P5，P6，…，则点P2019的坐标是（　　）
A．（4，0） B．（﹣2，2） C．（2，﹣4） D．（﹣4，2）
【解答】解：设P1（x，y），
∵点P（0，2）关于A的对称点为P1，即A是线段PP1的中点，
∵点A（1，﹣1），
∴1，1，解得x＝2，y＝﹣4，
∴P1（2，﹣4）．
同理可得，P1（2，﹣4），P2（﹣4，2），P3（4，0），P4（﹣2，﹣2），P5（0，0），P6（0，2），P7（2，﹣4），…，…，
∴每6个坐标循环一次．
∵336…3，
∴点P2019的坐标是（4，0）．
故选：A．
二、填空题（每空3分，共18分）
7．（6分）若3，则a＝　9　．
【解答】解：∵3，
∴a＝9，
故答案为：9．
8．（3分）命题“对顶角相等”的题设是　两个角为对顶角　．
【解答】解：命题“对顶角相等”的题设是两个角为对顶角．
故答案为两个角为对顶角．
9．（3分）10.1，则±　±1.01　．
【解答】解：∵10.1，
∴±±1.01，
故答案为：±1.01．
10．（6分）如图三角形ABC平移后得到三角形DEF，若AE＝11，DB＝5，则平移的距离是 　3　．

【解答】解：∵三角形ABC平移后得到三角形DEF，
∴AB＝DE，
∵AE＝11，DB＝5，
∴AD＝BE（11﹣5）＝3，
∴平移的距离是3，
故答案为：3．
11．（3分）如图，围棋盘放在某平面直角坐标系内，已知黑棋（甲）的坐标为（﹣2，1），黑棋（乙）的坐标为（﹣1，﹣2），则白棋（甲）的坐标是　（3，﹣1）　．

【解答】解：如图：
白棋（甲）的坐标是（3，﹣1），
故答案为：（3，﹣1）．

12．（3分）一副直角三角尺叠放如图1所示，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动（旋转角不超过180度），使两块三角尺至少有一组边互相平行．如图2：当∠BAD＝15°时，BC∥DE．则∠BAD（0°＜∠BAD＜180°）其它所有可能符合条件的度数为 　45°，60°，105°，135°　．

【解答】解：如图，

当AC1∥DE时，∠B1AD＝∠DAE＝45°；
当B2C2∥AD时，∠DAB＝∠B＝60°；
当BC∥AE时，∵∠EAB3＝∠B3＝60°，∴∠B3AD＝∠DAE+∠EAB3＝45°+60°＝105°；
当AB4∥DE时，∵∠E＝∠EAB4＝90°，∴∠B4AD＝∠DAE+∠EAB4＝45°+90°＝135°．
故答案为：45°，60°，105°，135°．
三、解答题（共84分）
13．（6分）计算：
（1）﹣22|﹣5|；
（2）．
【解答】解：（1）﹣22|﹣5|
＝﹣4+6+（﹣1）﹣5
＝﹣4．

（2）
＝（1）+（2）
1+2
＝1．
14．（6分）解方程或方程组
（1）4x2﹣16＝0；
（2）．
【解答】解：（1）移项得：4x2＝16，
系数化为1得：x2＝4，
开方得：x＝±2．
（2）将x＝y﹣3代入第二个方程得：y+2（y﹣3）＝6，
解得y＝4，
∴x＝y﹣3＝1．
∴方程组的解是．
15．（6分）已知是m+3的算术平方根，，求的值．
【解答】解：根据题意，得：，
解得，
所以n1，
故的值﹣1．
16．（6分）如图，已知：AD⊥BC于D，EG⊥BC于G，∠E＝∠1．求证：AD平分∠BAC．

【解答】证明：∵AD⊥BC于D，EG⊥BC于G，（已知）
∴∠ADC＝∠EGC＝90°，
∴AD∥EG，（同位角相等，两直线平行）．
∴∠1＝∠2，（两直线平行，内错角相等）．
∠E＝∠3（两直线平行，同位角相等）
又∵∠E＝∠1（已知）
∴∠2＝∠3，（等量代换）．
∴AD平分∠BAC．（角平分线的定义）
17．（6分）如图，要修建一条公路，从A村沿北偏东75°方向到B村，从B村沿北偏西25°方向到C村．若要保持公路CE与AB的方向一致，求∠ECB的度数．

【解答】解：由题意得：
∠ABC＝180°﹣75°﹣25°＝80°，
∵CE∥AB，
∴∠ECB＝∠ABC＝80°，
∴∠ECB的度数为80°．
18．（8分）在平面直角坐标系中，点A的坐标是（3a﹣5，a+1）
（1）若点A在y轴上，求a的值及点A的坐标．
（2）若点A到x轴的距离与到y轴的距离相等；求a的值及点A的坐标．
【解答】解：（1）∵点A在y轴上，
∴3a﹣5＝0，
解得：a，
a+1，
点A的坐标为：（0，）；
（2）∵点A到x轴的距离与到y轴的距离相等，
∴|3a﹣5|＝|a+1|，
①3a﹣5＝a+1，解得：a＝3，则点A（4，4）；
②3a﹣5+（a+1）＝0，解得：a＝1，则点A（﹣2，2）；
所以a＝3，则点A（4，4）或a＝1，则点A（﹣2，2）．
19．（8分）如图，直线AB与CD相交于点O，∠AOM＝90°，且OM平分∠NOC．若∠BOC＝4∠NOB，求∠MON的度数．

【解答】解：设∠NOB＝x，∠BOC＝4x，
∵∠BOC＝4∠NOB，
∴∠CON＝∠COB﹣∠BON＝4x﹣x＝3x，
∵OM平分∠CON，
∴∠MON∠CONx，
∵∠AOM＝90°，
∴∠BOM＝∠MON+∠NOBx+x＝90°，
∴x＝36，
∴∠MONx36°＝54°，
即∠MON的度数为54°．
20．（8分）如图，三角形ABO中，A（﹣2，﹣3）、B（2，﹣1），三角形A′B′O′是三角形ABO平移之后得到的图形，并且O的对应点O′的坐标为（4，3）．
（1）求三角形ABO的面积；
（2）作出三角形ABO平移之后的图形三角形A′B′O′，并写出A′、B′两点的坐标分别为A′　（2，0）　，B′　（6，2）　；
（3）P（x，y）为三角形ABO中任意一点，则平移后对应点P′的坐标为　（x+4，y+3）　．

【解答】解：（1）S△ABO＝4×32×32×14×2＝4；

（2）如图所示三角形A′B′O′为所求，

点A′（2，0），点B′（6，2），
故答案为：（2，0），（6，2）．

（3）点P′的坐标为（x+4，y+3）．
故答案为：（x+4，y+3）．
21．（8分）甲、乙两位同学在解方程组时，甲把字母a看错了得到方程组的解为；乙把字母b看错了得到方程组的解为．
（1）求a，b的正确值；
（2）求原方程组的解．
【解答】解：（1）根据题意得：，
解得：，
（2）将代入方程组，得，
解得．
答：（1）a，b的正确值分别为a＝2，b＝﹣3；
（2）原方程的解为．
22．（10分）在平面直角坐标系xOy中，对于任意三点A，B，C的“矩面积”，给出如下定义：“水平底”d是任意两点横坐标差的最大值；“铅垂高”h是任意两点纵坐标差的最大值，则“矩面积”S＝dh．例如：A，B，C三点的坐标分别为（1，2），（﹣3，1），（2，﹣2），则“水平底”d＝5，“铅垂高”h＝4，“矩面积”S＝dh＝20．根据所给定义解决下面的问题：
（1）若点D，E，F的坐标分别为（﹣1，2），（2，﹣1），（0，6），求这三点的“矩面积”S；
（2）已知点D（﹣1，2），E（2，﹣2），在x轴上是否存在点F，使这三点的“矩面积”S为20？若存在，求出点F的坐标；若不存在，请说明理由．
【解答】解：（1）∵点D，E，F的坐标分别为（﹣1，2），（2，﹣1），（0，6），
∴“水平底”d＝3，“铅垂高”h＝7，
∴这三点的“矩面积”S＝3×7＝21；
（2）假设存在 点F，设F（x，0），
∵点D（﹣1，2），E（2，﹣2），D，E，F三点的“矩面积”S为20，
∴“铅垂高”h＝4，
∴S＝dh＝d×4＝20，
∴d＝5，
①当x＞0时，“水平底”d＝x﹣（﹣1）＝x+1＝5，x＝4，
②当x＜0时，“水平底”d＝2﹣x＝5，x＝﹣3，
∴点F的坐标为（4，0）或（﹣3，0）．
23．（12分）材料1：反射定律
当入射光线MO照射到平面镜上时，将遵循平面镜反射定律，即反射角（∠NOH）的大小等于入射角（∠MOH）的大小，显然，这两个角的余角也相等，其中法线（OH）与平面镜（GF）垂直，并且满足入射光线（MO）、反射光线（ON）与法线在同一个平面．
材料2：平行逃逸角
对于某定角∠AOB＝α（0°＜α＜90°），点P为边OB上一点，从点P发出一光线PQ（射线），其角度为∠BPQ＝β（0°＜β＜90°），当光线PQ接触到边OA和OB时会遵循反射定律发生反射，当光线PQ经过n次反射后与边OA或OB平行时，称角β为定角α的n阶平行逃逸角，特别地，当光线PQ直接与OA平行时，称角β为定角α的零阶平行逃逸角．
（1）已知∠AOB＝α＝25°，
①如图1，若PQ∥OA，则∠BPQ＝　25　°，即该角为α的零阶平行逃逸角；
②如图2，经过一次反射后的光线P1Q∥OB，此时的∠BPP1为α的平行逃逸角，求∠BPP1的大小；
③若经过两次反射后的光线与OA平行，请补全图形，并求出α的二阶平行逃逸角；
（2）根据（1）的结论，归纳猜想对于任意角α（0°＜α＜90°），其n（n为自然数）阶平行逃逸角β＝　（n+1）α　（用含n和α的代数式表示）．


【解答】解：（1）①如图①中，∵PQ∥OA，
∴∠BPQ＝∠AOB＝25°，

故答案为25．

②如图2中，

∵P1Q∥OB，
∴∠AP1Q＝∠PP1O＝∠AOB＝25°，
∴∠BPP1＝∠AOB+∠PP1O＝50°．

③如图3中，如图所示，α的二阶平行逃逸角为25°×3＝75°，


（2）由（1）可知：α的零阶平行逃逸角为α，α的1阶平行逃逸角为2α，α的二阶平行逃逸角为3α，
…，由此可以推出，α的n阶平行逃逸角为（n+1）α，
故答案为（n+1）α．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/5/25 13:06:06；用户：朱文磊；邮箱：fywgy23@xyh.com；学号：21522783