安徽省九年级2022中考数学冲刺复习-05选择题提升必刷60题②

这是一份安徽省九年级2022中考数学冲刺复习-05选择题提升必刷60题②，共18页。

05选择题提升必刷60题②


一十四．由实际问题抽象出一元二次方程（共4小题）
23．（2022•马鞍山一模）电影《长津湖》真实生动地诠释了中国人民伟大的抗美援朝精神，一上映就受到观众的追捧，第一天票房收入2.05亿元，前三天的票房累计收入达到10.53亿元．若每天票房收入的增长率都为x，依题意可列方程（　　）
A．2.05（1+x）＝10.53
B．2.05（1+x）2＝10.53
C．2.05+2.05（1+x）2＝10.53
D．2.05+2.05（1+x）+2.05（1+x）2＝10.53
24．（2022•庐江县二模）原价为100元的某种药品经过连续两次降价后为64元，设平均每次降价的百分率为x，则下面所列方程正确的是（　　）
A．100（1﹣x）2＝64 B．64（1﹣x）2＝100
C．100（1﹣2x）＝64 D．64（1﹣2x）＝100
25．（2022•安庆模拟）某工厂计划用两年时间使产值增加到目前的4倍，并且使第二年增长的百分数是第一年增长百分数的2倍，设第一年增长的百分数为x，则可列方程得（　　）
A．（1+x）2＝4 B．x（1+2x+4x）＝4
C．2x（1+x）＝4 D．（1+x）（1+2x）＝4
26．（2022•宣州区一模）疫情期间居民为了减少外出时间，更愿意使用APP在线上购物，某购物APP今年二月份用户比一月份增加了44%，三月份用户比二月份增加了21%，求二、三两个月用户的平均每月增长率．设二、三两个月平均增长率为x，下列方程正确的是（　　）
A．2（1+x）2＝（1+44%）（1+21%）
B．（1+2x）2＝（1+44%）（1+21%）
C．（1+x）2＝（1+44%）（1+21%）
D．1+（1+x）+（1+x）2＝（1+44%）（1+21%）
一十五．不等式的性质（共2小题）
27．（2022•淮北模拟）若实数a，b，c满足a+b+c＞0，a+c＝2b，则下列结论中正确的是（　　）
A．b＜0，b2﹣ac≥0 B．b＞0，b2﹣ac≤0
C．b＞0，b2﹣ac≥0 D．b＜0，b2﹣ac≤0
28．（2022•安徽模拟）已知实数x，y，z满足x﹣y＝y﹣z＞0，且x+z＝0，则下列选项正确的是（　　）
A．x＜0 B．y＞0 C．x+y＜0 D．y•z＝0
一十六．函数关系式（共1小题）
29．（2022•安徽模拟）刘老师每天从家去学校上班行走的路程为1200米，某天他从家去学校上班时以每分钟40米的速度行走了前半程，为了不迟到他加快了速度，以每分钟50米的速度行走完了剩下的路程，那么刘老师距离学校的路程y（米）与他行走的时间t（分）（t＞15）之间的函数关系为（　　）
A．y＝﹣50t+1350 B．y＝50t﹣150
C．y＝﹣40t+1350 D．y＝﹣10t+1350
一十七．动点问题的函数图象（共3小题）
30．（2022•淮北模拟）如图，已知AB为半圆O的直径，AB＝6，点P为半圆O上一点（不与点A，B重合），PC⊥AB于点C，OD⊥BP，OE⊥AP，垂足分别为点D，E，若AC＝x，OE2+OD2＝y，则y与x的部分图象大致是（　　）

A． B．
C． D．
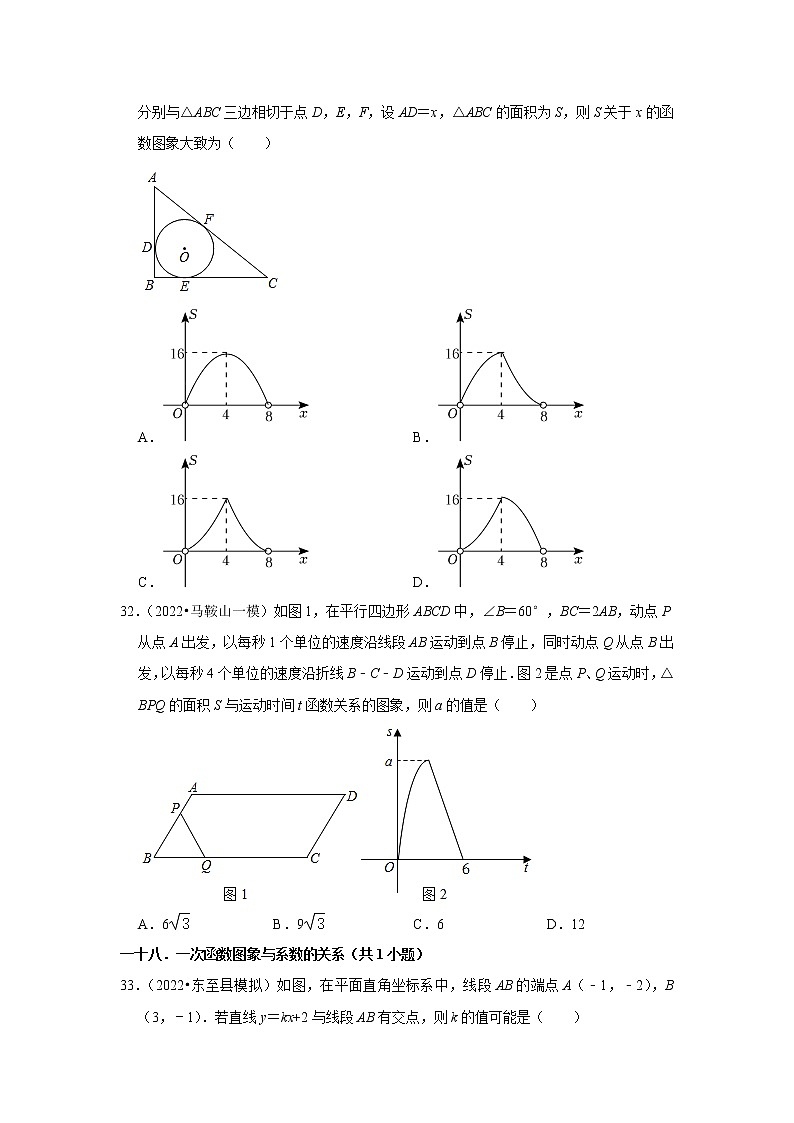
31．（2022•淮北一模）如图，在△ABC中，∠B＝90°，AC＝8，⊙O是△ABC的内切圆，分别与△ABC三边相切于点D，E，F，设AD＝x，△ABC的面积为S，则S关于x的函数图象大致为（　　）

A． B．
C． D．
32．（2022•马鞍山一模）如图1，在平行四边形ABCD中，∠B＝60°，BC＝2AB，动点P从点A出发，以每秒1个单位的速度沿线段AB运动到点B停止，同时动点Q从点B出发，以每秒4个单位的速度沿折线B﹣C﹣D运动到点D停止．图2是点P、Q运动时，△BPQ的面积S与运动时间t函数关系的图象，则a的值是（　　）

A．6 B．9 C．6 D．12
一十八．一次函数图象与系数的关系（共1小题）
33．（2022•东至县模拟）如图，在平面直角坐标系中，线段AB的端点A（﹣1，﹣2），B（3，﹣1）．若直线y＝kx+2与线段AB有交点，则k的值可能是（　　）

A．2 B．3 C． D．﹣4
一十九．一次函数的应用（共1小题）
34．（2022•蜀山区二模）“一方有难，八方支援”是中华民族的传统美德，在某次救援行动中，上午8时甲、乙两车同时从M地驶向N地，路程y（千米）与时间x（小时）的函数关系如图所示．甲车在上午10时30分到达N地，则下列说法错误的是（　　）

A．乙车先到达N地
B．乙车出发后小时追上甲车
C．甲、乙两车在出发后1小时相距最远
D．乙车在上午10时11分到达N地
二十．反比例函数图象上点的坐标特征（共1小题）
35．（2022•淮北一模）如图，直线y＝﹣x+2与x轴、y轴分别相交于A，B两点，过A，B两点作矩形ABCD，AB＝2AD，曲线在第一象限经过C，D两点，则k的值是（　　）

A．3 B．6 C．8 D．24
二十一．反比例函数与一次函数的交点问题（共1小题）
36．（2019•泸州）如图，一次函数y1＝ax+b和反比例函数y2＝的图象相交于A，B两点，则使y1＞y2成立的x取值范围是（　　）

A．﹣2＜x＜0或0＜x＜4 B．x＜﹣2或0＜x＜4
C．x＜﹣2或x＞4 D．﹣2＜x＜0或x＞4
二十二．二次函数图象与系数的关系（共1小题）
37．（2022•安徽二模）如图，二次函数y＝ax2+bx+c的图象经过（﹣1，1），且与y轴交于A点，过A点作AB∥x轴交抛物线于点B，且B点的横坐标为2，结合图象，则a的取值范围是（　　）

A． B． C． D．
二十三．平行线的性质（共3小题）
38．（2022•蜀山区二模）一副直角三角板如图摆放，点F在BC的延长线上，点D在AC上，∠B＝∠DFE＝90°，若
DE∥BF，则∠CDF的度数为（　　）

A．10° B．15° C．20° D．25°
39．（2022•淮北模拟）将两块三角板按如图所示位置摆放，若AD∥BC，点F在AD上，则∠ACF的度数为（　　）

A．15° B．10° C．20° D．25°
40．（2022•马鞍山一模）一副三角板按如图所示的位置摆放，若BC∥DE，则∠1的度数是（　　）

A．65° B．70° C．75° D．80°



【参考答案】
一十四．由实际问题抽象出一元二次方程（共4小题）
23．（2022•马鞍山一模）电影《长津湖》真实生动地诠释了中国人民伟大的抗美援朝精神，一上映就受到观众的追捧，第一天票房收入2.05亿元，前三天的票房累计收入达到10.53亿元．若每天票房收入的增长率都为x，依题意可列方程（　　）
A．2.05（1+x）＝10.53
B．2.05（1+x）2＝10.53
C．2.05+2.05（1+x）2＝10.53
D．2.05+2.05（1+x）+2.05（1+x）2＝10.53
【解析】解：设增长率为x，
依题意，得：2.05+2.05（1+x）+2.05（1+x）2＝10.53．
故选：D．
24．（2022•庐江县二模）原价为100元的某种药品经过连续两次降价后为64元，设平均每次降价的百分率为x，则下面所列方程正确的是（　　）
A．100（1﹣x）2＝64 B．64（1﹣x）2＝100
C．100（1﹣2x）＝64 D．64（1﹣2x）＝100
【解析】解：第一次降价后的价格为100×（1﹣x），第二次降价后价格为100×（1﹣x）×（1﹣x），
则列出的方程是100（1﹣x）2＝64．
故选：A．
25．（2022•安庆模拟）某工厂计划用两年时间使产值增加到目前的4倍，并且使第二年增长的百分数是第一年增长百分数的2倍，设第一年增长的百分数为x，则可列方程得（　　）
A．（1+x）2＝4 B．x（1+2x+4x）＝4
C．2x（1+x）＝4 D．（1+x）（1+2x）＝4
【解析】解：设第一年增长的百分数为x，则第二年增长的百分数为2x，
根据题意，得（1+x）（1+2x）＝4．
故选：D．
26．（2022•宣州区一模）疫情期间居民为了减少外出时间，更愿意使用APP在线上购物，某购物APP今年二月份用户比一月份增加了44%，三月份用户比二月份增加了21%，求二、三两个月用户的平均每月增长率．设二、三两个月平均增长率为x，下列方程正确的是（　　）
A．2（1+x）2＝（1+44%）（1+21%）
B．（1+2x）2＝（1+44%）（1+21%）
C．（1+x）2＝（1+44%）（1+21%）
D．1+（1+x）+（1+x）2＝（1+44%）（1+21%）
【解析】解：设二、三月份平均每月的增长率为x，
依题意，得：（1+x）2＝（1+44%）（1+21%）．
故选：C．
一十五．不等式的性质（共2小题）
27．（2022•淮北模拟）若实数a，b，c满足a+b+c＞0，a+c＝2b，则下列结论中正确的是（　　）
A．b＜0，b2﹣ac≥0 B．b＞0，b2﹣ac≤0
C．b＞0，b2﹣ac≥0 D．b＜0，b2﹣ac≤0
【解析】解：将a+c＝2b代入a+b+c＞0中得，
3b＞0，即b＞0，
由a+c＝2b可得b＝，
∴b2﹣ac＝（）2﹣ac＝，
∵（a﹣c）2≥0，
∴b2﹣ac≥0．
故选：C．
28．（2022•安徽模拟）已知实数x，y，z满足x﹣y＝y﹣z＞0，且x+z＝0，则下列选项正确的是（　　）
A．x＜0 B．y＞0 C．x+y＜0 D．y•z＝0
【解析】解：∵x﹣y＝y﹣z，
∴2y＝x+z，
∵x+z＝0，
∴2y＝0，
∴y＝0，
∴y•z＝0，故D选项符合题意，B选项不符合题意；
∵x﹣y＞0，y＝0，
∴x＞0，故A选项不符合题意；
∵x＞0，y＝0，
∴x+y＞0，故C选项不符合题意；
故选：D．
一十六．函数关系式（共1小题）
29．（2022•安徽模拟）刘老师每天从家去学校上班行走的路程为1200米，某天他从家去学校上班时以每分钟40米的速度行走了前半程，为了不迟到他加快了速度，以每分钟50米的速度行走完了剩下的路程，那么刘老师距离学校的路程y（米）与他行走的时间t（分）（t＞15）之间的函数关系为（　　）
A．y＝﹣50t+1350 B．y＝50t﹣150
C．y＝﹣40t+1350 D．y＝﹣10t+1350
【解析】解：∵以每分钟40米的速度行走了前半程，
∴以每分钟40米的速度行走了600米，
∴600÷40＝15（分），
∴剩下路程所需时间为（t﹣15）分，
∴1200﹣y＝600+50（t﹣15），
整理得y＝﹣50t+1350，
故选：A．
一十七．动点问题的函数图象（共3小题）
30．（2022•淮北模拟）如图，已知AB为半圆O的直径，AB＝6，点P为半圆O上一点（不与点A，B重合），PC⊥AB于点C，OD⊥BP，OE⊥AP，垂足分别为点D，E，若AC＝x，OE2+OD2＝y，则y与x的部分图象大致是（　　）

A． B．
C． D．
【解析】解：连接DE，OP，
∵AB为半圆的直径，
∴∠APB＝90°，
∵OE⊥AP，OD⊥BP，
∴四边形ODPE为矩形，
∴DE＝OP＝3，
在Rt△ABC中，
OE2+OD2＝DE2，
∴y＝OE2+OD2
＝OP2
＝32
＝9（0＜x＜6），
故选：A．
31．（2022•淮北一模）如图，在△ABC中，∠B＝90°，AC＝8，⊙O是△ABC的内切圆，分别与△ABC三边相切于点D，E，F，设AD＝x，△ABC的面积为S，则S关于x的函数图象大致为（　　）

A． B．
C． D．
【解析】解：连接OD、OE，如图，设⊙O的半径为r，
∵△ABC的内切圆O，分别与AB、BC、AC相切于点D、E、F，
∴OD⊥AB，OE⊥BC，AF＝AD＝x，CE＝CF＝8﹣x，
易得四边形ODBE为正方形，
∴DB＝BE＝OD＝r，
∵S＝r（AB+CB+AC）＝r（x+r+r+8﹣x+8）＝r2+8r，
∵AB2+BC2＝AC2，
∴（x+r）2+（8﹣x+r）2＝82，
∴r2+8r＝﹣x2+8x
∴S＝﹣x2+8x
＝﹣（x﹣4）2+16（0＜x＜8）．
故选：A．

32．（2022•马鞍山一模）如图1，在平行四边形ABCD中，∠B＝60°，BC＝2AB，动点P从点A出发，以每秒1个单位的速度沿线段AB运动到点B停止，同时动点Q从点B出发，以每秒4个单位的速度沿折线B﹣C﹣D运动到点D停止．图2是点P、Q运动时，△BPQ的面积S与运动时间t函数关系的图象，则a的值是（　　）

A．6 B．9 C．6 D．12
【解析】解：由题图2得，t＝6时点P停止运动，
∴点P以每秒1个单位速度从点A运动到点B用了6秒，
∴AB＝1×6＝6，
∴BC＝2AB＝12，
由点P和点Q的运动可知，AP＝t，BP＝6﹣t，
当点Q在BC上时，即0≤t＜3时，BQ＝4t，过点P作PM⊥BC于点M，

∵∠B＝60°，
∴PM＝BP•sinB＝（6﹣t），
此时△BPQ的面积＝BQ•PM＝•4t•（6﹣t）＝﹣t2+6t，
当点Q在CD上时，即3≤t≤6时，

∵四边形ABCD是平行四边形，
∴AB∥CD，
∴S△BPQ＝S△BPC＝BC•PM＝×12×（6﹣t）＝﹣3t+18，
由上可知，当点Q到达点C时，S＝a，
即当t＝3时，a＝﹣3×3+18＝9，
故选：B．
一十八．一次函数图象与系数的关系（共1小题）
33．（2022•东至县模拟）如图，在平面直角坐标系中，线段AB的端点A（﹣1，﹣2），B（3，﹣1）．若直线y＝kx+2与线段AB有交点，则k的值可能是（　　）

A．2 B．3 C． D．﹣4
【解析】解：由题意得，﹣k+2＜﹣2或3k+2＜﹣1，
解得k＞4或k＜﹣1，
∴符合条件的k的取值范围为k＞4或k＜﹣1，
∴选项A，B，C不符合题意，选项D符合题意，
故选：D．
一十九．一次函数的应用（共1小题）
34．（2022•蜀山区二模）“一方有难，八方支援”是中华民族的传统美德，在某次救援行动中，上午8时甲、乙两车同时从M地驶向N地，路程y（千米）与时间x（小时）的函数关系如图所示．甲车在上午10时30分到达N地，则下列说法错误的是（　　）

A．乙车先到达N地
B．乙车出发后小时追上甲车
C．甲、乙两车在出发后1小时相距最远
D．乙车在上午10时11分到达N地
【解析】解：A、由甲车在上午10时30分到达N地可知，线段OA﹣AB表示甲的路程y（千米）与时间x（小时）的函数关系，从而可得乙车先到达N地，故A正确，不符合题意；
B、由乙1小时行驶32千米可知线段OC的函数关系式为y＝32x，
由A（1，40），B（2.5，70）可得线段AB的函数关系式为y＝20x+20，
解32x＝20x+20得：x＝，
∴乙车出发后小时追上甲车，故B正确，不符合题意；
C、由图象可知，出发后1小时甲、乙两车相距40﹣32＝8（千米），
而乙车到达N地时，甲、乙两车相距70﹣（20×+20）＝（千米），
∴甲、乙两车在出发后1小时相距最远，故C正确，不符合题意；
D、在y＝32x中，令y＝70得x＝，
∴乙车用小时到达N地，即乙车到达N的时间是10时11.25分，故D错误，符合题意；
故选：D．
二十．反比例函数图象上点的坐标特征（共1小题）
35．（2022•淮北一模）如图，直线y＝﹣x+2与x轴、y轴分别相交于A，B两点，过A，B两点作矩形ABCD，AB＝2AD，曲线在第一象限经过C，D两点，则k的值是（　　）

A．3 B．6 C．8 D．24
【解析】解：作DH⊥x轴于H，
将y＝0代入直线y＝﹣x+2得﹣x+2＝0，
解得：x＝2．
∴点A的坐标为（2，0）．
将x＝0代入直线y＝﹣x+2得；y＝2，
∴点B的坐标为（0，2），
∴OA＝2，OB＝2，
∵∠BAD＝90°，
∴∠DAH+∠BAO＝90°．
∵∠BAO+∠ABO＝90°，
∴∠DAH＝∠ABO．
又∵∠DHA＝∠BOA＝90°，
∴△ADH∽△BAO，
∴＝＝＝，即＝＝．
∴DH＝AH＝1．
∴点D的坐标为（3，1）．
∵曲线在第一象限经过D点，
∴k＝3×1＝3，
故选：A．

二十一．反比例函数与一次函数的交点问题（共1小题）
36．（2019•泸州）如图，一次函数y1＝ax+b和反比例函数y2＝的图象相交于A，B两点，则使y1＞y2成立的x取值范围是（　　）

A．﹣2＜x＜0或0＜x＜4 B．x＜﹣2或0＜x＜4
C．x＜﹣2或x＞4 D．﹣2＜x＜0或x＞4
【解析】解：观察函数图象可发现：当x＜﹣2或0＜x＜4时，一次函数图象在反比例函数图象上方，
∴使y1＞y2成立的x取值范围是x＜﹣2或0＜x＜4．
故选：B．
二十二．二次函数图象与系数的关系（共1小题）
37．（2022•安徽二模）如图，二次函数y＝ax2+bx+c的图象经过（﹣1，1），且与y轴交于A点，过A点作AB∥x轴交抛物线于点B，且B点的横坐标为2，结合图象，则a的取值范围是（　　）

A． B． C． D．
【解析】解：由题意可知抛物线的对称轴为直线x＝1，
∵二次函数y＝ax2+bx+c的图象经过（﹣1，1），
∴，
∴，
∴y＝ax2﹣2ax+1﹣3a，
∵x＝﹣3时，y＜0，
∴9a+6a+1﹣3a＜0，
解得a＜﹣，
故选：A．
二十三．平行线的性质（共3小题）
38．（2022•蜀山区二模）一副直角三角板如图摆放，点F在BC的延长线上，点D在AC上，∠B＝∠DFE＝90°，若
DE∥BF，则∠CDF的度数为（　　）

A．10° B．15° C．20° D．25°
【解析】解：由题意得：∠ACB＝60°，∠EDF＝45°，
∵DE∥BF，
∴∠EDC＝∠ACB＝60°，
∴∠CDF＝∠EDC﹣∠EDF＝15°．
故选：B．
39．（2022•淮北模拟）将两块三角板按如图所示位置摆放，若AD∥BC，点F在AD上，则∠ACF的度数为（　　）

A．15° B．10° C．20° D．25°
【解析】解：由题意得∠DFE＝60°，
∵AD∥BC，∠ACB＝45°，
∴∠DAC＝∠ACB＝45°，
∵∠DFE是△AFC的外角，
∴∠DFE＝∠DAC+∠ACF，
∴∠ACF＝60°﹣45°＝15°．
故选：A．
40．（2022•马鞍山一模）一副三角板按如图所示的位置摆放，若BC∥DE，则∠1的度数是（　　）

A．65° B．70° C．75° D．80°
【解析】解：如图所示：
∵BC∥DE，
∴∠2＝∠B＝45°，
∴∠1＝∠2+∠D＝45°+30°＝75°．
故选：C．