苏科版九年级上册1.3 一元二次方程的根与系数的关系课前预习课件ppt

这是一份苏科版九年级上册1.3 一元二次方程的根与系数的关系课前预习课件ppt，文件包含13一元二次方程的根与系数的关系pptx、13一元二次方程根与系数的关系doc、补充习题13一元二次方程的根与系数的关系docx等3份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

1.探索一元二次方程的根与系数的关系. （难点） 2.不解方程的情况下利用一元二次方程的根与系数的关系解决问题. （重点）
写出一元二次方程的一般式：2. 一元二次方程求根公式.
ax2＋bx＋c＝0(a≠0)
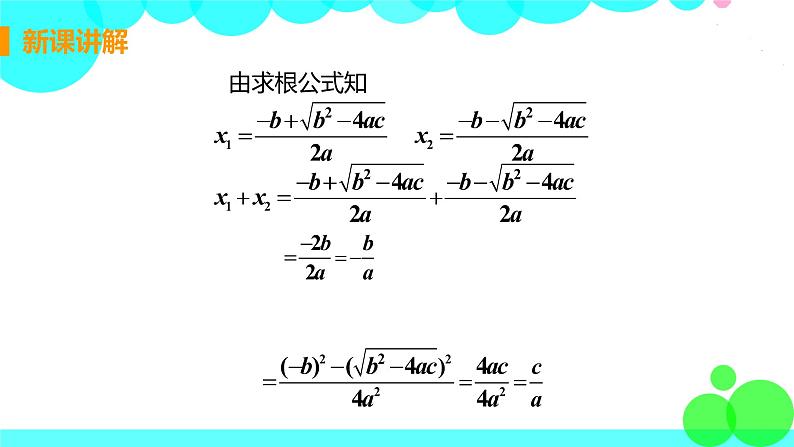
方程ax2＋bx＋c＝0(a≠0)的求根公式 不仅表示可以由方程的系数a，b，c决定根的值，而且反映了根与系数之间的联系， 一元二次方程根与系数之间的联系还有其他表现方式吗?
知识点1 一元二次方程的根与系数的关系
【思考1】 从因式分解法可知，方程(x－x1)(x－x2)＝0 ( x1，x2为已知数 ) 的两根为 x1 和 x2，将方程化为x2＋px＋q＝0的形式，你能看出x1，x2与p，q之间的关系吗?
方程两个根的和、积与系数分别有如下关系： x1＋x2＝－p，x1x2＝q.
【思考2】 一般的一元二次方程ax2＋bx＋c＝0中，二次项系数a未必是1， 它的两个根的和、积与系数又有怎样的关系呢?
1 根据一元二次方程的根与系数的关系，求 下列方程两个根x1，x2的和与积： (1) x2－6x－15＝0 (2) 3x2＋7x－9＝0； (3) 5x－1＝4x2. 解： (1)x1＋x2＝－(－6)＝6，x1x2＝－15. (3)方程化为4x2－5x＋1＝0，　　　　　
若x1，x2是一元二次方程x2 －4x－5＝0的两根，则x1·x2的值为(　　)A．－5 　　 　B．5　　 　C．－4 　 D．4已知x1，x2是一元二次方程x2－2x＝0的两个实数根，则下列结论错误的是(　　)A．x1 ≠ x2 　　 　B． x12－2x1＝0 C．x1＋x2 ＝2 D． x1• x2 ＝2
不解方程，求下列方程两个根的和与积：(1) x2－3x＝15； (2) 3x2＋2＝1－4x；(3) 5x2－1＝4x2＋x；(4) 2x2－x＋2＝3x＋1.
　解：(1)方程化为x2－3x－15＝0， x1＋x2＝－(－3)＝3，x1x2＝－15.
知识点2 一元二次方程根与系数关系的应用
2 已知一元二次方程x2－6x＋q＝0有一个根为2， 求方程的另一个根和 q 的值．分析：利用两根之和与积求解
解： 设这个方程的另一个根为m，则 ∵m＋2＝6，2m＝q. ∴ m＝4， q＝8. 当q ＝8时，Δ=(-6)2-4×8=4＞0， ∴另一个根为4，q的值为8.
若方程ax2+bx+c=0(a≠0)的两个根分别为x1，x2，则
若方程x2+px+q=0有两个实根x1，x2，则
x1+x2= -p, x1x2=q.
1. 早期，甲肝流行，传染性很强，曾有 2 人同时患上甲肝.在一天内，一人平均能传染 x 人，经过两天传染后 128 人患上甲肝，则 x 的值为( )
A.10 B.9 C.8 D.7
分析：依题意得 2+2x+x(2+2x)=128，解得 x1=7，x2=-9(不合题意，舍去)．故 x 的值为7．
2. 参加足球联赛的每两队之间都进行了两次比赛（双循环比赛），共要比赛90场，共有多少个队参加了比赛？
解：设共有x个队参加了比赛. 依题意x(x-1)=90. 解得x1=10, x2=-9(舍去).答：共有10个队参加了比赛.
3.两个相邻偶数的积是168.求这两个偶数的和．
解：设较小的偶数为 x，则另一个偶数为 (x+2)，依题意，得 x(x+2)=168，解得 x1=12，x2=-14，∴x+2=14或 x+2=-12，∴x+(x+2)=±26．答：这两个偶数的和为±26．