初中1.4 二次函数的应用教课课件ppt

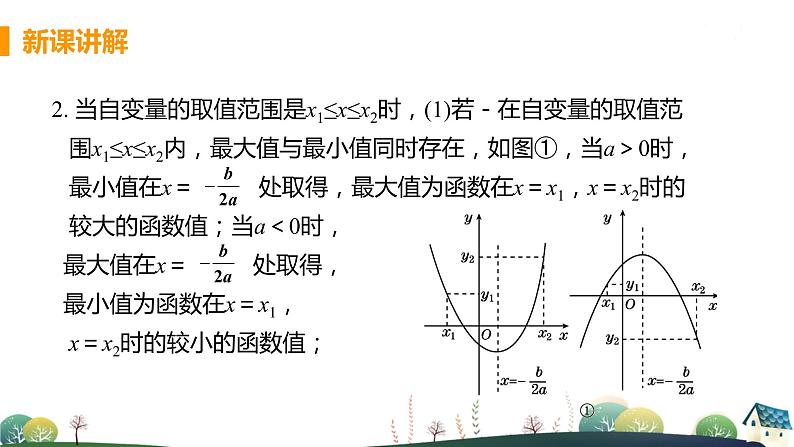
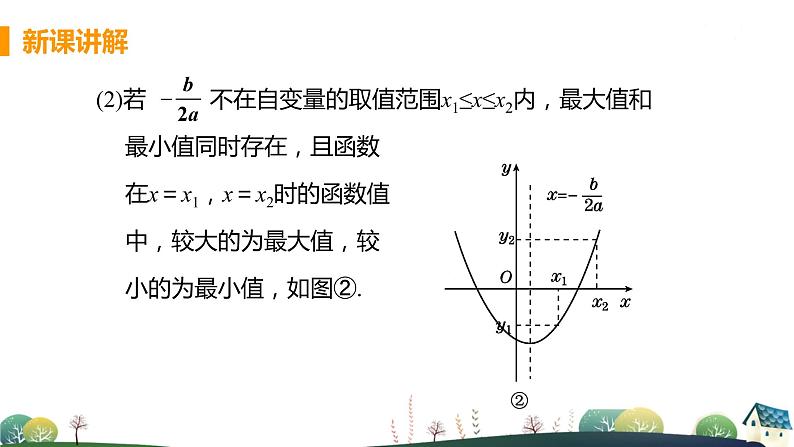
这是一份初中1.4 二次函数的应用教课课件ppt，文件包含第1课时二次函数最值问题pptx、第2课时球类运动路线及拱桥问题pptx、14二次函数的应用docx、电子教案第1课时二次函数最值问题doc、电子教案第2课时球类运动路线及拱桥问题doc等5份课件配套教学资源，其中PPT共49页， 欢迎下载使用。
1.建立坐标系解抛物线形运动问题.（重点）2.建立坐标系解抛物线形建筑问题.（重点、难点）
知识点1 建立坐标系解抛物线形运动问题
活动问题：（1）运动中的距离、时间、速度问题，这类问题多根据运动规律中的公式求解.（2）物体的运动路线（轨迹）问题，解决这类问题的思想方法是利用数形结合思想和函数思想，合理建立直角坐标系，根据已知数据，运用待定系数法求出运动轨迹（抛物线）对应的函数表达式，再利用二次函数的性质去分析、解决问题.
如图所示，是某防空部队进行射击演习时在平面直角坐标系中的示意图，位于地面上O点正上方 千米的A处的直升机向目标C发射防空导弹，已知目标C距地面2.25千米，与点O的水平距离为7千米．若导弹运行到距地面最大高度为3千米时相应的水平距离为4千米(即图中的点D)，如果导弹的运行轨迹是抛物线形，请你判断按轨迹 飞行的导弹能否击中目标C，并说明理由．
由题意可知抛物线的顶点坐标为(4，3)，且经过点A 故可设顶点式y＝a(x－h)2＋k求出抛物线对应函数的表达式，然后看点C是否在抛物线上即可．设抛物线对应函数的表达式为y＝a(x－h)2＋k.根据题意得，抛物线的顶点D的坐标为(4，3)．∴y＝a(x－4)2＋3.
把A 的坐标代入上式得： ＝a(0－4)2＋3， 解得a＝∴抛物线对应函数的表达式为 y＝ (x－4)2＋3，即y＝ x2＋ x＋ . 当x＝7时，y＝ ×72＋ ×7＋ ＝2.25.∴点C(7，2.25)在抛物线上． 即按轨迹飞行的导弹能击中目标C.
知识点2 建立坐标系解抛物线形建筑问题
一个涵洞的截面边缘是抛物线，如图所示. 现测得当水面宽AB= 1.6m时，涵洞顶点与水面的距离为2. 4 m.这时，离开水面1. 5 m处，涵洞宽ED是多少? 是否会超过1 m?
根据已知条件，要求涵洞的宽ED,只要求出FD的长度即可，即在上图所示的平面直角坐标系 中，求出点D的横坐标.因为点D在涵洞截面的抛物线上，又由已知条件可 得到点D的纵坐标，所以利用抛物线所对应的函数表达式可以进一步算出点D的横坐标.
抛物线形建筑物问题： 几种常见的抛物线形建筑物有拱形桥洞、隧道洞口、拱形门等，解决这类问题的关键是根据已知条件选择合理的位置建立直角坐标系，结合问题中的数据求出函数表达式，然后利用函数表达式解决问题
如图，某企业的大门是抛物线形，大门底部的宽AB为4 m，顶端C距离地面的高度为4.4 m，一辆载满货物的汽车要通过大门，货物顶部距底部2.8m，装货的宽度为2.4 m，这辆汽车能否顺利通过大门？为什么？
根据题意先建立合适的平面直角坐标系，运用二次函数的性质解答．
解法一：以AB的中点为坐标原点，以AB所在的直线为x轴，以线段AB的垂直平分线为y轴建立平面直角坐标系，如图所示，根据题意得：点B的坐标为(2，0)，点C的坐标为(0，4.4)．设抛物线对应函数的表达式为y＝ax2＋k.把B(2，0)，C(0，4.4)的坐标代入，
得 解得∴抛物线对应函数的表达式为y＝－1.1x2＋4.4. 当x＝ ＝1.2时，y＝－1.1×1.22＋4.4＝2.816＞2.8.∴这辆汽车能顺利通过大门．
解法二：以点A为坐标原点，以AB所在的直线为x轴，以过点A与AB垂直的直线为y轴建立平面直角坐标系，如图所示，根据题意得：点B的坐标为(4，0)，点C的坐标为(2，4.4)．
∵抛物线经过原点，∴设抛物线对应函数的表达式为y＝ax2＋bx. 把B(4，0)，C(2，4.4)的坐标代入 得 解得∴抛物线对应函数的表达式为y＝－1.1x2＋4.4x. 当x＝ ＝0.8时， y＝－1.1×0.82＋4.4×0.8＝2.816＞2.8.∴这辆汽车能顺利通过大门．
1.运动问题：(1)运动中的距离、时间、速度问题； 这类问题多根据运动规律中的公式求解．(2)物 体的运动路线(轨迹)问题；解决这类问题的思想 方法是利用数形结合思想和函数思想，合理建立 直角坐标系，根据已知数据,运用待定系数法求 出运动轨迹(抛物线)的解析式，再利用二次函数 的性质去分析、解决问题．
2.抛物线型建筑物问题：几种常见的抛物线型建筑 物有拱形桥洞、隧道洞口、拱形门等．解决这类 问题的关键是根据已知条件选择合理的位置建立 直角坐标系，结合问题中的数据求出函数解析式， 然后利用函数解析式解决问题．
1 某广场有一喷水池，水从地面喷出，如图，以水平 地面为x轴，出水点为原点，建立平面直角坐标系， 水在空中划出的曲线是抛物线y＝－x2＋4x(单位：m) 的一部分，则水喷出的最大高度是(　　) A．4 m B．5 m C．6 m D．7 m
2.足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线，不考虑空气阻力，足球距离地面的高度h(单位：m)与足球被踢出后经过的时间t(单位：s)之间的关系如下表：
下列结论：①足球距离地面的最大高度为20 m；②足球飞行路线的对称轴是直线t＝ ；③足球被踢出9 s时落地；④足球被踢出1.5 s时，距离地面的高度是11 m．其中正确结论的个数是(　　)A．1 B．2 C．3 D．4