2022年广西玉林市玉州区中考数学一模试卷

这是一份2022年广西玉林市玉州区中考数学一模试卷，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022年广西玉林市玉州区中考数学一模试卷
一、选择题：本大题共12小题，每小题3分，共36分。在每小题给出的四个选项中，只有一项是符合题目要求的，把正确答案的标号填（涂）在答题卡内相应的位置上。
1．（3分）﹣2022的绝对值是（　　）
A． B．2022 C． D．﹣2022
2．（3分）2022年2月北京冬奥会在全球社交平台上已吸引了超30亿网民的关注，一些明星运动员账号的互动量超过10亿条．毫无疑问，北京冬奥会已经成为迄今为止收视率和网络关注度最高的全球顶流赛事之一．数字10亿用科学记数法表示为（　　）
A．10×108 B．1×109 C．1×1010 D．1×108
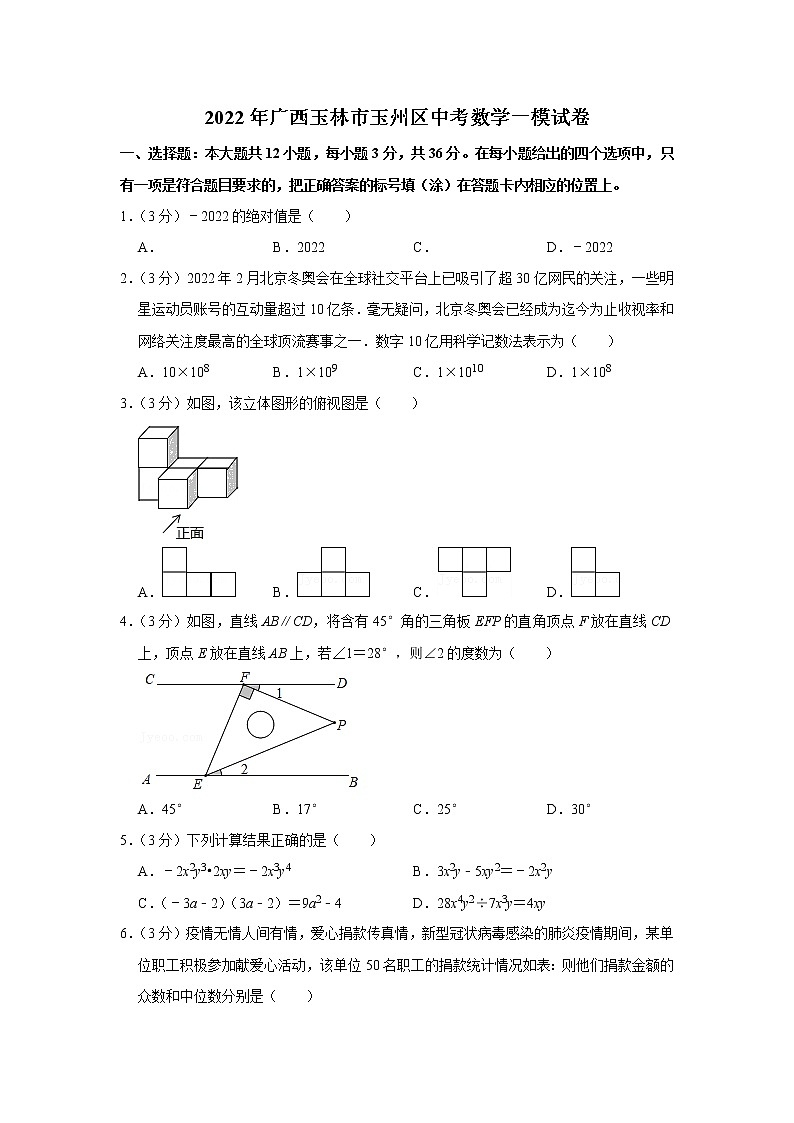
3．（3分）如图，该立体图形的俯视图是（　　）

A． B． C． D．
4．（3分）如图，直线AB∥CD，将含有45°角的三角板EFP的直角顶点F放在直线CD上，顶点E放在直线AB上，若∠1＝28°，则∠2的度数为（　　）

A．45° B．17° C．25° D．30°
5．（3分）下列计算结果正确的是（　　）
A．﹣2x2y3•2xy＝﹣2x3y4 B．3x2y﹣5xy2＝﹣2x2y
C．（﹣3a﹣2）（3a﹣2）＝9a2﹣4 D．28x4y2÷7x3y＝4xy
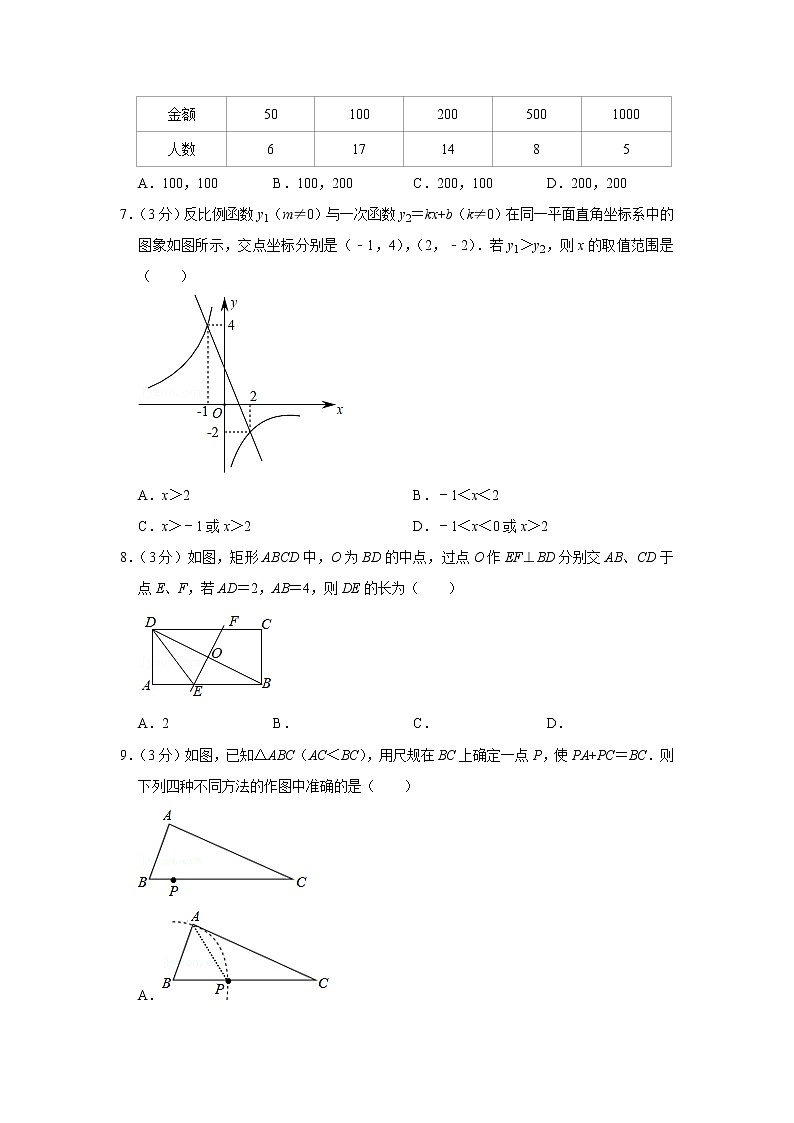
6．（3分）疫情无情人间有情，爱心捐款传真情，新型冠状病毒感染的肺炎疫情期间，某单位职工积极参加献爱心活动，该单位50名职工的捐款统计情况如表：则他们捐款金额的众数和中位数分别是（　　）
金额
50
100
200
500
1000
人数
6
17
14
8
5
A．100，100 B．100，200 C．200，100 D．200，200
7．（3分）反比例函数y1（m≠0）与一次函数y2＝kx+b（k≠0）在同一平面直角坐标系中的图象如图所示，交点坐标分别是（﹣1，4），（2，﹣2）．若y1＞y2，则x的取值范围是（　　）

A．x＞2 B．﹣1＜x＜2
C．x＞﹣1或x＞2 D．﹣1＜x＜0或x＞2
8．（3分）如图，矩形ABCD中，O为BD的中点，过点O作EF⊥BD分别交AB、CD于点E、F，若AD＝2，AB＝4，则DE的长为（　　）

A．2 B． C． D．
9．（3分）如图，已知△ABC（AC＜BC），用尺规在BC上确定一点P，使PA+PC＝BC．则下列四种不同方法的作图中准确的是（　　）

A．
B．
C．
D．
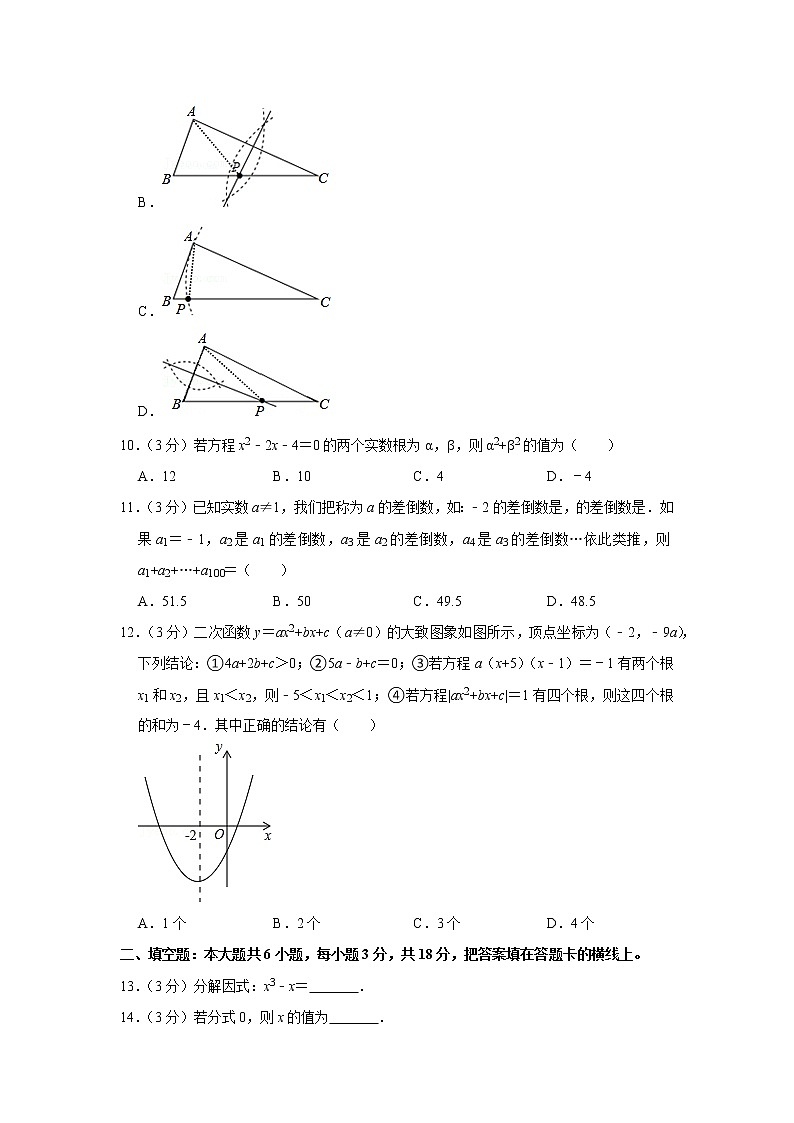
10．（3分）若方程x2﹣2x﹣4＝0的两个实数根为α，β，则α2+β2的值为（　　）
A．12 B．10 C．4 D．﹣4
11．（3分）已知实数a≠1，我们把称为a的差倒数，如：﹣2的差倒数是，的差倒数是．如果a1＝﹣1，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数…依此类推，则a1+a2+…+a100＝（　　）
A．51.5 B．50 C．49.5 D．48.5
12．（3分）二次函数y＝ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为（﹣2，﹣9a），下列结论：①4a+2b+c＞0；②5a﹣b+c＝0；③若方程a（x+5）（x﹣1）＝﹣1有两个根x1和x2，且x1＜x2，则﹣5＜x1＜x2＜1；④若方程|ax2+bx+c|＝1有四个根，则这四个根的和为﹣4．其中正确的结论有（　　）

A．1个 B．2个 C．3个 D．4个
二、填空题：本大题共6小题，每小题3分，共18分，把答案填在答题卡的横线上。
13．（3分）分解因式：x3﹣x＝　 　．
14．（3分）若分式0，则x的值为　 　．
15．（3分）一个多边形的内角和是1080°，这个多边形的边数是　 　．
16．（3分）从2021年起，江苏省高考采用“3+1+2”模式：“3”是指语文、数学、外语3科为必选科目，“1”是指在物理、历史2科中任选1科，“2”是指在化学、生物、思想政治、地理4科中任选2科．若小玲在“1”中选择了历史，在“2”中已选择了地理，则她选择生物的概率是　 　．
17．（3分）如图，在平行四边形ABCD中，AB＜AD，∠D＝30°，CD＝4，以AB为直径的⊙O交BC于点E，则阴影部分的面积为　 　．

18．（3分）如图，在平面直角坐标系xOy中，函数y（k＞0，x＞0）的图象经过菱形OACD的顶点D和边AC的中点E，若菱形OACD的边长为3，则k的值为　 　．

三、解答题：本大题共8小题，满分共66分，解答过程写在答题卡上，解答应写出文字说明，证明过程或演算步骤。
19．（6分）计算：（﹣2）2+||﹣3tan30°+（2020﹣π）0．
20．（6分）先化简再从1，0，﹣1这三个数中选个合适的数作为x的值代入求值．
21．（8分）如图，四边形ABCD是平行四边形，延长AD至点E，使DE＝AD，连接BD、CE．
（1）求证：四边形BCED是平行四边形；
（2）若DA＝DB＝4，cosA，求点B到点E的距离．

22．（8分）湘江中学九年级开展了“读一本好书”的活动，通过抽样对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”“戏剧”“散文”“其他”四个类别，每位同学仅选一项，根据调查结果绘制了如图不完整的频数分布表和扇形统计图．
类别
频数（人数）
频率
小说

0.5
戏剧
4

散文
10
0.25
其他
6

合计
m
1
请根据以上信息，解答下列问题：
（1）计算：m＝　 　；
（2）在扇形统计图中，“戏剧”类所占的百分比为　 　；
（3）在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从中任意选出2名同学参加学校的戏剧社团，请用画树状图或列表的方法，求选取的2人恰好是乙和丙的概率．

23．（8分）如图，在Rt△ABC中，∠ACB＝90°，D为AB的中点，以CD为直径的⊙O分别交AC，BC于点E，F两点，过点F作FG⊥AB于点G．
（1）试判断FG与⊙O的位置关系，并说明理由；
（2）若AC＝6，CD＝5，求FG的长．

24．（8分）为美化小区环境，物业计划安排甲、乙两个工程队完成小区绿化工作．已知甲工程队每天绿化面积是乙工程队每天绿化面积的2倍，甲工程队单独完成600m2的绿化面积比乙工程队单独完成600m2的绿化面积少用2天．
（1）求甲、乙两工程队每天绿化的面积分别是多少m2；
（2）小区需要绿化的面积为9600m2，物业需付给甲工程队每天绿化费为0.3万元，付给乙工程队每天绿化费为0.2万元，若要使这次的绿化总费用不超过12万元，则至少应安排甲工程队工作多少天？
25．（10分）如图，在边长为4的正方形ABCD中，点E为对角线AC上一动点（点E与点A、C不重合），连接DE，作EF⊥DE交射线BA于点F，过点E作MN∥BC分别交CD、AB于点M、N，作射线DF交射线CA于点G．
（1）求证：EF＝DE；
（2）当AF＝2时，求GE的长．

26．（12分）如图，抛物线yx2x+4交x轴于小，B两点（点B在A的右边），与y轴交于点C，连接AC，BC．点P是第一象限内抛物线上的一个动点，点P的横坐标为m，过点P作PM⊥x轴，垂足为点M，PM交BC于点Q．
（1）求A、B两点坐标；
（2）过点P作PN上BC，垂足为点N，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？
（3）试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标，若不存在，请说明理由．


2022年广西玉林市玉州区中考数学一模试卷
参考答案与试题解析
一、选择题：本大题共12小题，每小题3分，共36分。在每小题给出的四个选项中，只有一项是符合题目要求的，把正确答案的标号填（涂）在答题卡内相应的位置上。
1．（3分）﹣2022的绝对值是（　　）
A． B．2022 C． D．﹣2022
【解答】解：﹣2022的绝对值是：2022．
故选：B．
2．（3分）2022年2月北京冬奥会在全球社交平台上已吸引了超30亿网民的关注，一些明星运动员账号的互动量超过10亿条．毫无疑问，北京冬奥会已经成为迄今为止收视率和网络关注度最高的全球顶流赛事之一．数字10亿用科学记数法表示为（　　）
A．10×108 B．1×109 C．1×1010 D．1×108
【解答】解：10亿＝1000000000＝1×109．
故选：B．
3．（3分）如图，该立体图形的俯视图是（　　）

A． B． C． D．
【解答】解：如图所示的立体图形的俯视图是C．
故选：C．

4．（3分）如图，直线AB∥CD，将含有45°角的三角板EFP的直角顶点F放在直线CD上，顶点E放在直线AB上，若∠1＝28°，则∠2的度数为（　　）

A．45° B．17° C．25° D．30°
【解答】解：由题意得：∠EFP＝90°，∠FEP＝45°，
∵CD∥AB，
∴∠DFE+∠FEB＝180°，
∴∠1+∠2＝180°﹣90°﹣45°＝45°，
∵∠1＝28°，
∴∠2＝45°﹣28°＝17°，
故选：B．
5．（3分）下列计算结果正确的是（　　）
A．﹣2x2y3•2xy＝﹣2x3y4 B．3x2y﹣5xy2＝﹣2x2y
C．（﹣3a﹣2）（3a﹣2）＝9a2﹣4 D．28x4y2÷7x3y＝4xy
【解答】解：﹣2x2y3•2xy＝﹣4x3y4，故A错误，不符合题意；
3x2y与﹣5xy2不是同类项，不能合并，故B错误，不符合题意；
（﹣3a﹣2）（3a﹣2）＝4﹣9a2，故C错误，不符合题意；
28x4y2÷7x3y＝4xy，故D正确，符合题意；
故选：D．
6．（3分）疫情无情人间有情，爱心捐款传真情，新型冠状病毒感染的肺炎疫情期间，某单位职工积极参加献爱心活动，该单位50名职工的捐款统计情况如表：则他们捐款金额的众数和中位数分别是（　　）
金额
50
100
200
500
1000
人数
6
17
14
8
5
A．100，100 B．100，200 C．200，100 D．200，200
【解答】解：他们捐款金额的众数为100，中位数为200，
故选：B．
7．（3分）反比例函数y1（m≠0）与一次函数y2＝kx+b（k≠0）在同一平面直角坐标系中的图象如图所示，交点坐标分别是（﹣1，4），（2，﹣2）．若y1＞y2，则x的取值范围是（　　）

A．x＞2 B．﹣1＜x＜2
C．x＞﹣1或x＞2 D．﹣1＜x＜0或x＞2
【解答】解：由函数图象可知，当﹣1＜x＜0或x＞2时，一次函数的图象在反比例函数图象的下方．
故选：D．
8．（3分）如图，矩形ABCD中，O为BD的中点，过点O作EF⊥BD分别交AB、CD于点E、F，若AD＝2，AB＝4，则DE的长为（　　）

A．2 B． C． D．
【解答】解：根据题意可知：EF垂直平分BD，
∴EB＝ED，
∴AE＝AB﹣BE＝AB﹣ED＝4﹣DE，
根据勾股定理，得
DE2＝AE2+AD2，
∴DE2＝（4﹣DE）2+22，
解得DE．
故选：B．
9．（3分）如图，已知△ABC（AC＜BC），用尺规在BC上确定一点P，使PA+PC＝BC．则下列四种不同方法的作图中准确的是（　　）

A．
B．
C．
D．
【解答】解：A、如图所示：此时BA＝BP，则无法得出AP＝BP，故不能得出PA+PC＝BC，故此选项错误；
B、如图所示：此时PA＝PC，则无法得出AP＝BP，故不能得出PA+PC＝BC，故此选项错误；
C、如图所示：此时CA＝CP，则无法得出AP＝BP，故不能得出PA+PC＝BC，故此选项错误；
D、如图所示：此时BP＝AP，故能得出PA+PC＝BC，故此选项正确；
故选：D．
10．（3分）若方程x2﹣2x﹣4＝0的两个实数根为α，β，则α2+β2的值为（　　）
A．12 B．10 C．4 D．﹣4
【解答】解：∵方程x2﹣2x﹣4＝0的两个实数根为α，β，
∴α+β＝2，αβ＝﹣4，
∴α2+β2＝（α+β）2﹣2αβ＝4+8＝12；
故选：A．
11．（3分）已知实数a≠1，我们把称为a的差倒数，如：﹣2的差倒数是，的差倒数是．如果a1＝﹣1，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数…依此类推，则a1+a2+…+a100＝（　　）
A．51.5 B．50 C．49.5 D．48.5
【解答】解：∵a1＝﹣1，
∴a2，
a3，
a4，
∴这列数是以﹣1，，2依次循环，且﹣12，
∵100÷3＝33……1，
∴a1+a2+…+a100＝331＝48.5；
故选：D．
12．（3分）二次函数y＝ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为（﹣2，﹣9a），下列结论：①4a+2b+c＞0；②5a﹣b+c＝0；③若方程a（x+5）（x﹣1）＝﹣1有两个根x1和x2，且x1＜x2，则﹣5＜x1＜x2＜1；④若方程|ax2+bx+c|＝1有四个根，则这四个根的和为﹣4．其中正确的结论有（　　）

A．1个 B．2个 C．3个 D．4个
【解答】解：∵抛物线的顶点坐标（﹣2，﹣9a），
∴2，9a，
∴b＝4a，c＝﹣5a，
∴抛物线的解析式为y＝ax2+4ax﹣5a，
∴4a+2b+c＝4a+8a﹣5a＝7a＞0，故①正确，
5a﹣b+c＝5a﹣4a﹣5a＝﹣4a＜0，故②错误，
∵抛物线y＝ax2+4ax﹣5a交x轴于（﹣5，0），（1，0），
∴若方程a（x+5）（x﹣1）＝﹣1有两个根x1和x2，且x1＜x2，则﹣5＜x1＜x2＜1，正确，故③正确，
若方程|ax2+bx+c|＝1有四个根，设方程ax2+bx+c＝1的两根分别为x1，x2，则2，可得x1+x2＝﹣4，
设方程ax2+bx+c＝﹣1的两根分别为x3，x4，则2，可得x3+x4＝﹣4，
所以这四个根的和为﹣8，故④错误，
故选：B．
二、填空题：本大题共6小题，每小题3分，共18分，把答案填在答题卡的横线上。
13．（3分）分解因式：x3﹣x＝　x（x+1）（x﹣1）　．
【解答】解：x3﹣x，
＝x（x2﹣1），
＝x（x+1）（x﹣1）．
故答案为：x（x+1）（x﹣1）．
14．（3分）若分式0，则x的值为　x＝0　．
【解答】解：∵分式0，
∴x2﹣x＝0且x﹣1≠0，
∴x＝0．
故答案为：x＝0．
15．（3分）一个多边形的内角和是1080°，这个多边形的边数是　8　．
【解答】解：设多边形边数有x条，由题意得：
180（x﹣2）＝1080，
解得：x＝8，
故答案为：8．
16．（3分）从2021年起，江苏省高考采用“3+1+2”模式：“3”是指语文、数学、外语3科为必选科目，“1”是指在物理、历史2科中任选1科，“2”是指在化学、生物、思想政治、地理4科中任选2科．若小玲在“1”中选择了历史，在“2”中已选择了地理，则她选择生物的概率是　　．
【解答】解：在“2”中已选择了地理，从剩下的化学、生物，思想品德三科中选一科，因此选择生物的概率为；
故答案为：；
17．（3分）如图，在平行四边形ABCD中，AB＜AD，∠D＝30°，CD＝4，以AB为直径的⊙O交BC于点E，则阴影部分的面积为　　．

【解答】解：连接OE、AE，
∵AB是⊙O的直径，
∴∠AEB＝90°，
∵四边形ABCD是平行四边形，
∴AB＝CD＝4，∠B＝∠D＝30°，
∴AEAB＝2，BE2，
∵OA＝OB＝OE，
∴∠B＝∠OEB＝30°，
∴∠BOE＝120°，
∴S阴影＝S扇形OBE﹣S△BOE，
，
，
，
故答案为：．

18．（3分）如图，在平面直角坐标系xOy中，函数y（k＞0，x＞0）的图象经过菱形OACD的顶点D和边AC的中点E，若菱形OACD的边长为3，则k的值为　　．

【解答】解：过D作DQ⊥x轴于Q，过C作CM⊥x轴于M，过E作EF⊥x轴于F，
设D点的坐标为（a，b）则C点的坐标为（a+3，b），
∵E为AC的中点，
∴EFCMb，AFAMOQa，
E点的坐标为（3a，b），
把D、E的坐标代入y得：k＝ab＝（3a）b，
解得：a＝2，
在Rt△DQO中，由勾股定理得：a2+b2＝32，
即22+b2＝9，
解得：b（负数舍去），
∴k＝ab＝2，
故答案为：2．
三、解答题：本大题共8小题，满分共66分，解答过程写在答题卡上，解答应写出文字说明，证明过程或演算步骤。
19．（6分）计算：（﹣2）2+||﹣3tan30°+（2020﹣π）0．
【解答】解：（﹣2）2+||﹣3tan30°+（2020﹣π）0
＝431
＝5．
20．（6分）先化简再从1，0，﹣1这三个数中选个合适的数作为x的值代入求值．
【解答】解：原式＝（）

＝1+x，
∵x≠0，x≠1，
∴x＝﹣1，
当x＝﹣1时，原式＝1+（﹣1）＝0．
21．（8分）如图，四边形ABCD是平行四边形，延长AD至点E，使DE＝AD，连接BD、CE．
（1）求证：四边形BCED是平行四边形；
（2）若DA＝DB＝4，cosA，求点B到点E的距离．

【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AD＝BC，AD∥BC，
∵DE＝AD，
∴DE＝BC，DE∥BC，
∴四边形BCED是平行四边形；
（2）解：连接BE，
∵DA＝DB＝4，DE＝AD，
∴AD＝BD＝DE＝4，
∴∠ABE＝90°，AE＝8，
∵cosA，
∴AB＝2，
∴BE．

22．（8分）湘江中学九年级开展了“读一本好书”的活动，通过抽样对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”“戏剧”“散文”“其他”四个类别，每位同学仅选一项，根据调查结果绘制了如图不完整的频数分布表和扇形统计图．
类别
频数（人数）
频率
小说

0.5
戏剧
4

散文
10
0.25
其他
6

合计
m
1
请根据以上信息，解答下列问题：
（1）计算：m＝　40　；
（2）在扇形统计图中，“戏剧”类所占的百分比为　10%　；
（3）在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从中任意选出2名同学参加学校的戏剧社团，请用画树状图或列表的方法，求选取的2人恰好是乙和丙的概率．

【解答】解：（1）∵喜欢散文的有10人，频率为0.25，
∴m＝10÷0.25＝40；
故答案为：40；

（2）∵喜欢戏剧的有4人，
∴“戏剧”类所占的百分比为100%＝10%；
故答案为：10%；

（3）画树状图，如图所示：

所有等可能的情况有12种，其中恰好是乙与丙的情况有2种，
则P（乙和丙）．
23．（8分）如图，在Rt△ABC中，∠ACB＝90°，D为AB的中点，以CD为直径的⊙O分别交AC，BC于点E，F两点，过点F作FG⊥AB于点G．
（1）试判断FG与⊙O的位置关系，并说明理由；
（2）若AC＝6，CD＝5，求FG的长．

【解答】解：（1）FG与⊙O相切，
理由：如图，连接OF，
∵∠ACB＝90°，D为AB的中点，
∴CD＝BD，
∴∠DBC＝∠DCB，
∵OF＝OC，
∴∠OFC＝∠OCF，
∴∠OFC＝∠DBC，
∴OF∥DB，
∴∠OFG+∠DGF＝180°，
∵FG⊥AB，
∴∠DGF＝90°，
∴∠OFG＝90°，
∴FG与⊙O相切；
（2）连接DF，
∵CD＝5，
∴AB＝2CD＝10，
∴BC8，
∵CD为⊙O的直径，
∴∠DFC＝90°，
∴FD⊥BC，
∵DB＝DC，
∴BFBC＝4，
∵sin∠ABC，
即，
∴FG．

24．（8分）为美化小区环境，物业计划安排甲、乙两个工程队完成小区绿化工作．已知甲工程队每天绿化面积是乙工程队每天绿化面积的2倍，甲工程队单独完成600m2的绿化面积比乙工程队单独完成600m2的绿化面积少用2天．
（1）求甲、乙两工程队每天绿化的面积分别是多少m2；
（2）小区需要绿化的面积为9600m2，物业需付给甲工程队每天绿化费为0.3万元，付给乙工程队每天绿化费为0.2万元，若要使这次的绿化总费用不超过12万元，则至少应安排甲工程队工作多少天？
【解答】解：（1）设乙工程队每天能完成绿化的面积是x（m2），
根据题意得，
解得：x＝150，
经检验：x＝150是原方程的解，
则2x＝300．
答：甲工程队每天能完成绿化的面积是300m2，乙工程队每天能完成绿化的面积是150m2，

（2）设甲队工作y天完成：300y（m2），乙队完成工作所需要（天），
根据题意得：0.3y+0.212，
解得：y≥8．
所以y最小值是8．
答：至少应安排甲队工作8天．
25．（10分）如图，在边长为4的正方形ABCD中，点E为对角线AC上一动点（点E与点A、C不重合），连接DE，作EF⊥DE交射线BA于点F，过点E作MN∥BC分别交CD、AB于点M、N，作射线DF交射线CA于点G．
（1）求证：EF＝DE；
（2）当AF＝2时，求GE的长．

【解答】（1）证明：∵四边形ABCD是正方形，AC是对角线，
∴∠ECM＝45°，
∵MN∥BC，∠BCM＝90°，
∴∠NMC+∠BCM＝180°，∠MNB+∠B＝180°，
∴∠NMC＝90°，∠MNB＝90°，
∴∠MEC＝∠MCE＝45°，∠DME＝∠ENF＝90°，
∴MC＝ME，
∵CD＝MN，
∴DM＝EN，
∵DE⊥EF，∠EDM+∠DEM＝90°，
∴∠DEF＝90°，
∴∠DEM+∠FEN＝90°，
∴∠EDM＝∠FEN，
在△DME和△ENF中
，
∴△DME≌△ENF（ASA），
∴EF＝DE；
（2）解：如图1所示，由（1）知，△DME≌△ENF，
∴ME＝NF，
∵四边形MNBC是矩形，
∴MC＝BN，
又∵ME＝MC，AB＝4，AF＝2，
∴BN＝MC＝NF＝1，
∵∠EMC＝90°，
∴CE，
∵AF∥CD，
∴△DGC∽△FGA，
∴，
∴，
∵AB＝BC＝4，∠B＝90°，
∴AC＝4，
∵AC＝AG+GC，
∴AG，CG，
∴GE＝GC﹣CE；
如图2所示，
同理可得，FN＝BN，
∵AF＝2，AB＝4，
∴AN＝1，
∵AB＝BC＝4，∠B＝90°，
∴AC＝4，
∵AF∥CD，
∴△GAF∽△GCD，
∴，
即，
解得，AG＝4，
∵AN＝NE＝1，∠ENA＝90°，
∴AE，
∴GE＝GA+AE＝5．
综上所述：GE的长为：，5．


26．（12分）如图，抛物线yx2x+4交x轴于小，B两点（点B在A的右边），与y轴交于点C，连接AC，BC．点P是第一象限内抛物线上的一个动点，点P的横坐标为m，过点P作PM⊥x轴，垂足为点M，PM交BC于点Q．
（1）求A、B两点坐标；
（2）过点P作PN上BC，垂足为点N，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？
（3）试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标，若不存在，请说明理由．

【解答】解：（1）当y＝0，x2x+4＝0，解得x1＝﹣3，x2＝4，
∴A（﹣3，0），B（4，0），
（2）设点P（m，m2m+4），则点 Q（m，﹣m+4），
∵OB＝OC，
∴∠ABC＝∠OCB＝45°＝∠PQN，
P～N＝PQ•sin∠PQN（m2m+4+m﹣4）（m﹣2）2，
∵0，
∴PN有最大值，
当m＝2时，PN的最大值为．
（3）存在，理由：
点A、B、C的坐标分别为（﹣3，0）、（4，0）、（0，4），
则AC＝5，AB＝7，BC＝4，∠OBC＝∠OCB＝45°，
①当AC＝AQ时，如图，

则AC＝AQ＝5，
设：QM＝MB＝n，则AM＝7﹣n，
由勾股定理得：（7﹣n）2+n2＝25，解得：n＝3或4（舍去4），
故点Q（1，3）．
②当AC＝CQ时，如图，

CQ＝5，则BQ＝BC﹣CQ＝45，
则QM＝MB，
故点Q（，）．
③当CQ＝AQ时，
CQ＝BC﹣BQ＝4（4﹣m）m，
AQm，
即2m2﹣2m+25＝2m2，
解得m．
∵0＜m＜4，
∴m（舍去）．
综上所述点Q的坐标为：Q（1，3）或Q（，）．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/5/15 9:40:04；用户：朱文磊；邮箱：fywgy23@xyh.com；学号：21522783