2022年湖北省黄冈市中考全真模拟试题附答案

这是一份2022年湖北省黄冈市中考全真模拟试题附答案，共26页。试卷主要包含了单选题，填空题，综合题等内容，欢迎下载使用。
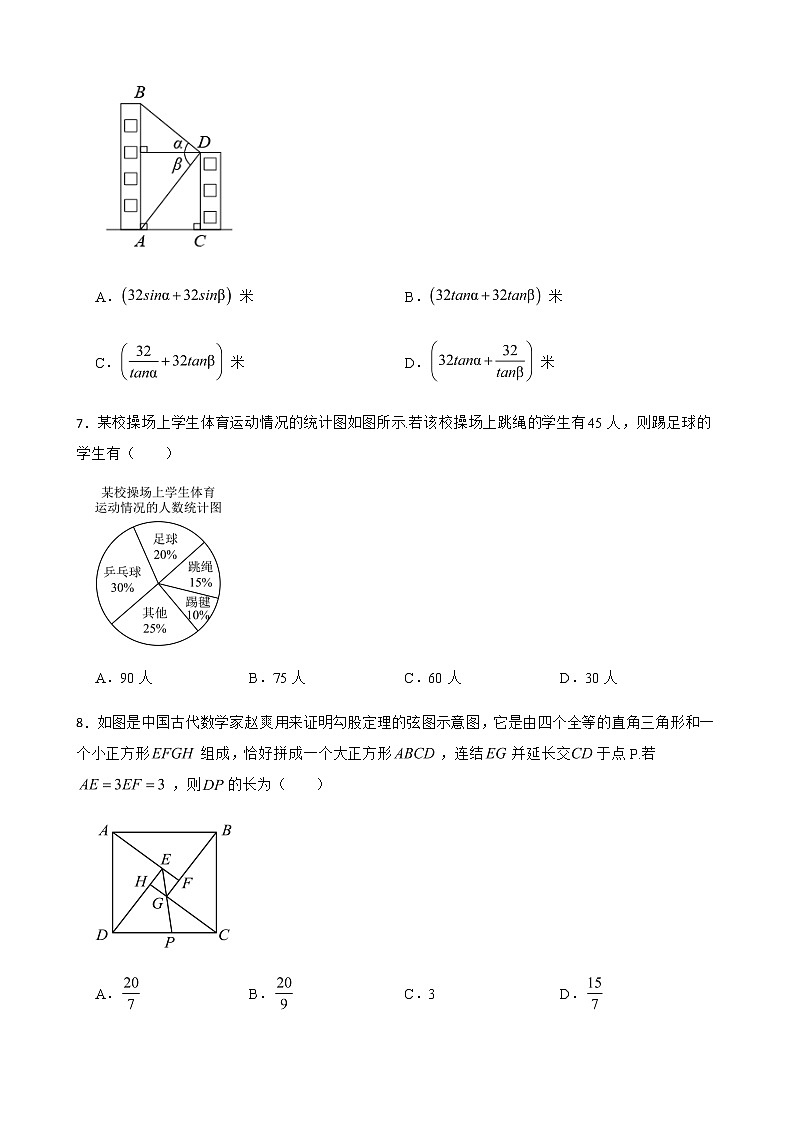
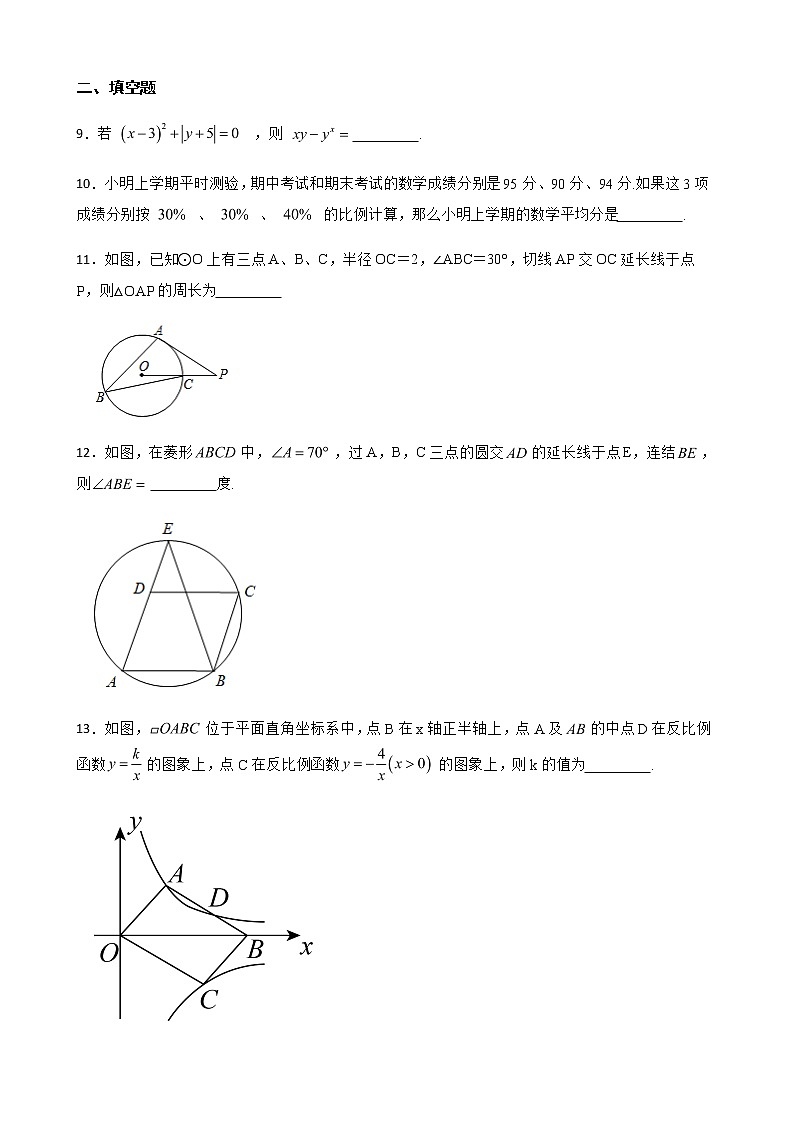
 中考全真模拟试题 一、单选题1．在四个数中，最小的是（　　）A．-3 B．0 C． D．-12．如图所示的几何体是由6个大小相同的小正方体组成，它的主视图为（　　）A． B． C． D．3．2021年12月9日，“天宫误堂”第一课正式开讲，时隔8年之后，中国航天员再次进行太空授课，此时空间站距离地球约370000米，数据370000用科学记数法表示为（　　） A． B． C． D．4．计算的正确结果是（　　）A． B． C． D．5．若扇形的圆心角为，半径为3，则该扇形的面积为（　　）A． B． C． D．6．如图，小华在屋顶D点时，测得对面图书馆顶部B的仰角为，图书馆底部A的俯角为，若这两幢楼的距离米，则图书馆楼高等于（　　）A．米 B．米C．米 D．米7．某校操场上学生体育运动情况的统计图如图所示.若该校操场上跳绳的学生有45人，则踢足球的学生有（　　）A．90人 B．75人 C．60人 D．30人8．如图是中国古代数学家赵爽用来证明勾股定理的弦图示意图，它是由四个全等的直角三角形和一个小正方形组成，恰好拼成一个大正方形，连结并延长交于点P.若，则的长为（　　）A． B． C．3 D．二、填空题9．若 ，则 　     　.  10．小明上学期平时测验，期中考试和期末考试的数学成绩分别是95分、90分、94分.如果这3项成绩分别按 、 、 的比例计算，那么小明上学期的数学平均分是　     　.11．如图，已知⊙O上有三点A、B、C，半径OC＝2，∠ABC＝30°，切线AP交OC延长线于点P，则△OAP的周长为　     　12．如图，在菱形中，，过A，B，C三点的圆交的延长线于点E，连结，则　     　度. 13．如图，位于平面直角坐标系中，点B在x轴正半轴上，点A及的中点D在反比例函数的图象上，点C在反比例函数的图象上，则k的值为　     　.14．如图，地面上两个村庄C、D处于同一水平线上，一飞行器在空中以12千米/小时的速度沿MN方向水平飞行，航线MN与C、D在同一铅直平面内.当该飞行器飞至村庄C的正上方A处时，测得∠NAD＝60°，该飞行器从A处飞行40分钟至B处时，测得∠ABD＝75°，则村庄C、D间的距离为　     　千米.（ ≈1.732，结果保留一位小数）  15．如图所示，将形状大小完全相同的“ ”按照一定的规律摆成下列图形：第1幅图中“   ”的个数为 ，第2幅图中“   ”的个数为 ，第3幅图中“ ”的个数为 ，…，以此类推．  （1）按照图中规律， 　     　；  （2）　         　．  16．如图，在平面直角坐标系中，点C是y轴正半轴上的一个动点，抛物线y＝ax2－6ax+5a（a是常数，且a＞0）过点C，与x轴交于点A、B，点A在点B的左边.连接AC，以AC为边作等边三角形ACD，点D与点O在直线AC两侧，连接BD，则BD的最小值是　     　.三、综合题17．（1）（x+2y）2﹣y（x+4y）；（2）（﹣1）÷．18．小亮是个集邮爱好者，他收集了如图所示的四张纪念邮票（除正面内容不同外，其余均相同），现将四张邮票背面朝上，洗匀放好（1）小亮从中随机抽取一张邮票是“冬奥会吉祥物冰墩墩”的概率是　     　（2）小亮从中随机抽取一张邮票（不放回），再从余下的邮票中随机抽取一张，求抽到的两张邮票恰好是“冬奥会会徽”和“冬奧会吉祥物冰墩墩”的概率．（这四张邮票从左到右依次分别用字母A、B、C、D表示）19．随着信息技术的迅猛发展，人们购物的支付方式更加多样、便捷，为调查大学生购物支付方式，某大学一份调查问卷，要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：（1）这次活动共调查了　     　人；在扇形统计图中，表示“支付宝”支付的扇形圆心角的度数为　     　（2）将条形统计图补充完整；（3）若该大学有10000名学生，请你估计购物选择用支付宝支付方式的学生约有多少人？20．冰墩墩（如图）是2022年北京冬季奥运会的吉祥物．某商店第一次用1200元购进冰墩墩手办若干个，第二次又用相同价格购进冰墩墩饰扣若干个，已知每个冰墩墩饰扣的进价是冰墩墩手办进价的，购进冰墩墩手办数量比饰扣少了10个．（1）冰墩墩饰扣的进价是多少元？（2）若冰墩墩饰扣的售价要比冰墩墩手办的售价少30元，且销售完毕后获利不低于1100元，问每个冰墩墩手办的售价至少是多少元？21．如图，点P为函数与函数图象的交点，点P的纵坐标为4，轴，垂足为点B．（1）求m的值；（2）点M是函数图象上一动点，过点M作于点D，若，求点M的坐标．22．如图1，在中，，AB是的直径，交AC于点D，过点D的直线交BC于点E，交AB的延长线于点P，PD是的切线． （1）求证：；（2）若，，求图中阴影部分的周长和面积；（3）如图2，，连接DM，交AB于点N，若，求的值． 23．某体育器材专卖店销售A，B两款篮球，已知A款篮球的销售单价比B款篮球多10元，且用4000元购买A款篮球的数量与用3600元购买B款篮球的数量相同．（1）A、B两款篮球的销售单价各是多少元？（2）由于需求量大，A、B两款篮球很快售完，该专卖店计划再次购进这两款篮球共100个，且A款篮球的数量不少于B款篮球数量的2倍．①求A款篮球至少有几个；②老板计划让利顾客，A款篮球8折出售，B款篮球的销售单价不变，且两款篮球的进价每个均为60元，应如何进货才能使这批篮球的销售利润最大，最大利润是多少元？24．定义：四边形ABCD中，AB=AC，∠BDC=∠BAC，则称四边形ABCD为半角四边形，边BC称为半对边.（1）如图①，若四边形ABCD为半角四边形，且BC为半对边，设∠DBC=α，用含有α的代数式表示∠ACD；（2）如图②，等腰△ABC，AB=AC，点D为其内部一点，∠ABD=∠ACD，连结AD，作△ACD的外接圆⊙O，BD的延长线交⊙O于点E，连结EA，EC，求证：四边形ABCE为半角四边形；（3）如图③，在（2）的条件下，延长BA交⊙O于点F，连结EF，EF∥BC.①求证：BC=CE；②若AD=3，BC=6，求四边形ADEF的面积.25．如图1，抛物线y＝﹣x2+bx+c经过点A（﹣1，0）、B（3，0）．（1）求抛物线的函数表达式：（2）设抛物线的顶点为D，与y轴相交与点C，连接AC、CD、BC、BD，请你判断∠ACO与∠DBC的数量关系，并说明理由；（3）如图2，连接AD，与BC相交于点E，点G是抛物线上一动点，在对称轴上是否存在点F，使得∠EFG=90°，且tan∠FEG=如果存在，请求出点F的坐标；如果不存在，请说明理由．答案解析部分1．【答案】A2．【答案】B3．【答案】D4．【答案】A5．【答案】C6．【答案】B7．【答案】C8．【答案】A9．【答案】11010．【答案】93.1分11．【答案】12．【答案】7513．【答案】214．【答案】5.515．【答案】（1）30（2）16．【答案】317．【答案】（1）解：（x+2y）2﹣y（x+4y）＝x2+4xy+4y2﹣xy﹣4y2＝x2+3xy；（2）解：（﹣1）÷＝•＝﹣•＝﹣．18．【答案】（1）（2）解：列树状图如下所示：由树状图可知一共有12种等可能性的结果数，其中抽到的两张邮票恰好是“冬奥会会徽”和“冬奧会吉祥物冰墩墩”的结果数有2种，∴抽到的两张邮票恰好是“冬奥会会徽”和“冬奧会吉祥物冰墩墩”的概率．19．【答案】（1）200；81°（2）解：使用微信的人数为：200×30%＝60，使用银行卡的人数为：200×15%＝30， 补充完整的条形统计图如图所示；（3）解：10000× ＝2250（人）， 答：购物选择用支付宝支付方式的学生约有2250人.20．【答案】（1）解：设冰墩墩手办的进价是x元，则每个冰墩墩饰扣的进价是元，根据题意列方程得，解得．经检验是原分式方程的解，则．答：冰墩墩饰扣的进价是40元．（2）解：设每个冰墩墩手办的售价是y元．根据题意列不等式得，解得．答：每个冰墩墩手办的售价至少是88元．21．【答案】（1）解；∵点P纵坐标为4，且在一次函数图象上，∴4=x+1，解得x=3，∴P(3，4)．又∵点P在反比例函数图象上，∴，解得；（2）解；∵，∴．设PD=t(t>0)，则DM=2t，分类讨论①当M点在P点右侧时，如图，∴M点的坐标为(3+2t，4−t)，∴，解得：(舍)∴，．∴此时M点的坐标为(8，)；②当M点在P点的左侧时，∴M点的坐标为(3−2t，4+t)，∴，解得：(均舍去)．故此情况不合题意．综上，M点的坐标为(8，)．22．【答案】（1）证明：如图1，连接OD． ∵PD是的切线，∴．∴．∵AB是的直径，∴．∴．∵，∴．∴．（2）解：∵，，， ∴．∴．∵，∴．∴△OBD为等边三角形．∴，．∵AB是的直径，∴．∴，．又∵，∴，，．∴阴影部分的周长为，阴影部分的面积为．∴阴影部分周长为，面积为．（3）解：如图2，连接OM，过点D作于点F． ∵，∴．∵，∴．∴．∵，∴．设，则．由勾股定理得．由三角形的面积公式得．∴．∵，，∴∠MON=∠DFN=90°，又∠ONM=∠FND，∴．∴．又∵，，∴．即．23．【答案】（1）解：设B款篮球的单价是a元，则A款篮球的单价是（a+10）元， 根据题意得 ，解得，a＝90，经检验，a＝90是原分式方程的解，则a+10＝100，答：A、B两款篮球的销售单价分别是100元、90元（2）解：①设购买A款篮球x个，则购买B款篮球（100﹣x）个，
∵A款篮球的数量不少于B款篮球数量的2倍，
∴x≥2（100﹣x），
解得，x≥，
∵x为正整数，
∴A款篮球至少有67个；
②设销售利润为w元，
则w＝（100×0.8﹣60）x+（90﹣60）（100﹣x）＝﹣10x+3000
∵﹣10＜0，
∴w随x的增大而减小，
∴当x＝67时，w取得最大值，此时w＝2330，100﹣x＝33，
答：当购买A款篮球67个，B款篮球33个时，能使这批篮球的销售利润最大，最大利润是2330元．24．【答案】（1）解：设∠ABD=β，
∵AB=AC，∠DBC=α，
∴∠ABC= ∠ACB=α+β，
∴∠BAC=180°-2（α+β），∵四边形ABCD为半角四边形，BC为半对边，
∴∠BDC=∠BAC=90°-（α+β），
∴∠BCD=180°-∠BDC-∠DBC=180°-90°+（α+β）-α=90°+β，
∴∠ACD=∠BCD-∠ACB=90°+β-（α+β）=90°-α；（2）证明：∵AB=AC，
∴∠ABC=ACB，
∵∠ACD=∠ABD，
∴∠DBC=∠DCB，
∴BD=CD，
又∵AD=AD，
∴△ABD≌△ACD（SAS），
∴∠CAD=∠BAD=∠BAC，
又∵弧CD=弧DC，
∴∠DAC=∠DEC，
∴∠DEC=∠BAC，
∴∠BEC=∠BAC，
∴四边形ABCE为半角四边形；（3）①证明：如图③，

设∠ABD=β，∠DBC=α，
∵AB=AC，
∴∠BAC=180°-2（α+β），
∴∠FEC=180°-2（α+β），
∵四边形ABCE为半角四边形，
∴∠BEC=∠BAC=[180°-2（α+β）]=90°-（α+β），
∴∠FEB=∠FEC-∠BEC=180°-2（α+β）-90°+（α+β）=90°-（α+β），
∴∠BEC=∠FEB，
又∵EF∥BC，
∴∠FEB=∠EBC，
∴∠BEC=∠EBC，
∴BC=CE；

②解：如图④，延长AD交BC于点H，过点E作EG垂直BF于点G，AC与BE交于点M，

由（2）可知：∠BEC=∠EBC，∠BEC=∠BAC，
设∠BEC=∠EBC=α，
∴∠BAC=2α，
又∵△ABD≌△ACD，
∴∠BAD=∠CAD=a，BD=DC，
∴∠DBC=∠DCB=α，
∵AB=AC，
∴AH⊥BC，BH=HC=BC=×6=3，
∵∠BHD=∠AHB=90°，∠DBH=∠BAH=α，
∴△BHD∽△AHB，
∴，
∴AH2-3AH-18=0，
解得：AH=6，
∴DH=3，
∴BD==3，AB=AC==3，
∵∠HCA=90°-α，由（1）中结论可得∠ACE=90°-α，BC=CE，
∴CA⊥BE，BM=ME，
∴易证△BHD∽△AHB，
∴，
即，
∴AM=，DM=，
∴DE=5，
∴S△ADE=AM·DE=××5=，
∵∠EGB=∠ABM，∠G=∠AMB，
∴△EGB∽△AMB，
∴，即，
∴EG=，BG=，
∵四边形FACE为圆内接四边形，
∴∠EFG=∠ACE=90°-α，
∴∠EFG=∠ACH，
∴△EGF∽△AHC，
∴，即，
∴GF=，
∴AF=BG-AB-GF=-3=，
∴S△AFE=AF·EG=××=4，
∴S四边形ADEF=S△AFE+S△ADE=4+=.25．【答案】（1）解：将点代入得：，解得：，所以抛物线解析式为；（2）解：，，令，则，，，，，，，是直角三角形，，，；（3）解：存在点，使得，且，理由如下：抛物线的对称轴为直线，设直线的解析式为，得，，解得：，设直线AD的解析式为，可得，，解得：，，联立方程组，解得：，，设，如图1，当G点在对称轴的右侧，F点在E点下方时，过点F作MN⊥y轴，过E点作EM⊥x轴交MN于点M，过点G作GN⊥MN交于N点，，，，，，，，，，（舍去），，；如图2，当G点对称轴的左侧，F点在E点下方时，过E点作EK垂直对称轴交于点K，过点F作FH⊥y轴，过点G作GH⊥HF交于H，，，， ，，，，，，，，，，解得：或（舍去），；如图3，当F点在E点上方时，此时G点在对称轴的右侧，过点F作轴，过点E作EP⊥PQ交于点P，过点G作GQ⊥PQ交于点Q，，，，，，，，，，，，，，解得：，，，综上可得：点的坐标为或或．