2021-2022长郡集团中考模拟四套数学试题含答案

这是一份2021-2022长郡集团中考模拟四套数学试题含答案，文件包含2021-2022长郡一模docx、2021-2022长郡二模pdf、2021-2022长郡自主模考二答案docx、2021-2022长郡自主模拟六pdf、2021-2022长郡自主模考二pdf、2021-2022长郡自主模考三pdf、2021-2022长郡二模答案pdf、2021-2022长郡自主模拟六答案DOCX、2021-2022长郡自主模考三答案docx等9份试卷配套教学资源，其中试卷共70页， 欢迎下载使用。
2022年湖南省长沙市长郡教育集团中考数学一模试卷
一、选择题（在下列各题的四个选项中，只有一项是符合题意的．请在答题卡中填涂符合题意的选项．本大题共10个小题，每小题3分，共30分）
1．（3分）下列四个数中，最小的数是（　　）
A．0 B．−12022 C．2022 D．﹣2022
2．（3分）下面四个化学仪器示意图中，是轴对称图形的是（　　）
A． B． C． D．
3．（3分）2021年9月20日“天舟三号”在海南成功发射，这是中国航天工程又一重大突破，它的运行轨道距离地球393000米，数据393000米用科学记数法表示为（　　）
A．0.393×107米 B．3.93×106米
C．3.93×105米 D．39.3×104米
4．（3分）如图所示正三棱柱的主视图是（　　）

A． B． C． D．
5．（3分）如图，点D，E分别在∠ABC的边BA，BC上，DE⊥AB，过BA上的点F（位于点D上方作FG∥BC，若∠AFG＝42°，则∠DEB的度数为（　　）

A．42° B．48° C．52° D．58°
6．（3分）一次函数y＝﹣x﹣2的图象经过（　　）
A．第一、二、三象限 B．第一、二、四象限
C．第一、三、四象限 D．第二、三、四象限
7．（3分）为了落实“作业、睡眠、手机、读物、体质”等五项管理要求，了解学生的睡眠状况，调查了一个班50名学生每天的睡眠时间，绘成睡眠时间频数分布直方图如图所示，则所调查学生睡眠时间的众数，中位数分别为（　　）

A．7h 7h B．8h 7.5h C．7h 7.5h D．8h 8h
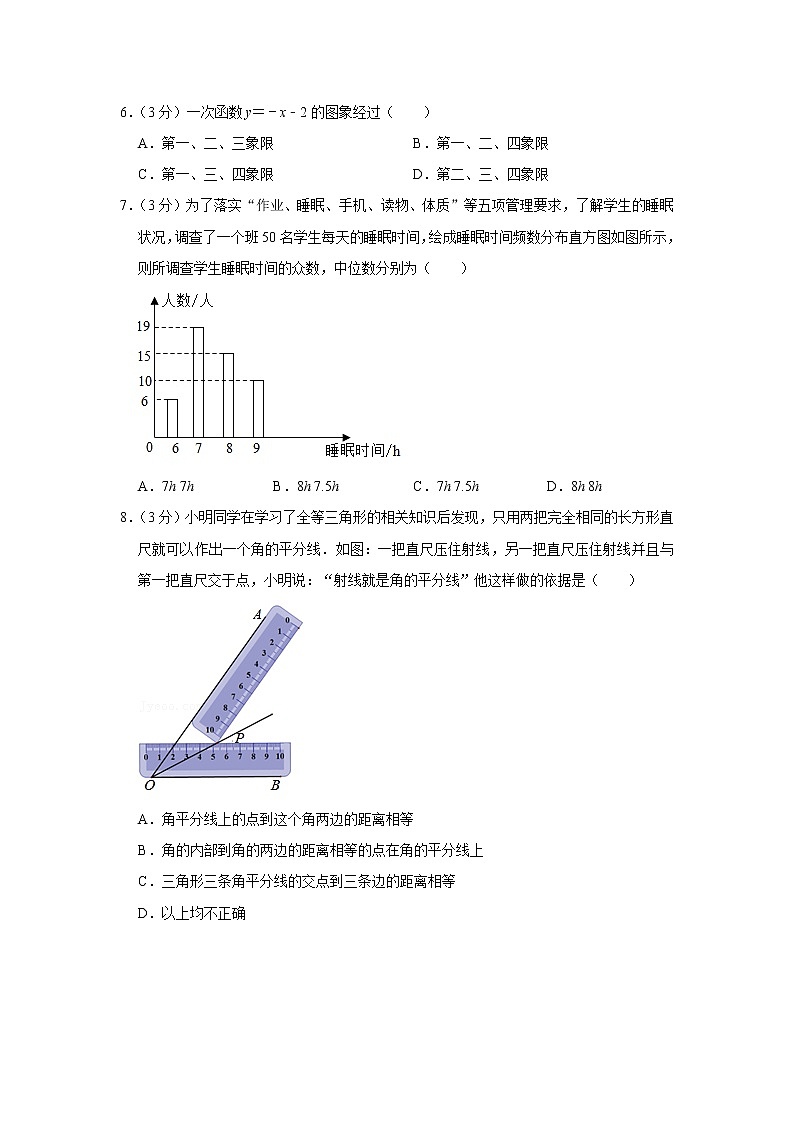
8．（3分）小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线，另一把直尺压住射线并且与第一把直尺交于点，小明说：“射线就是角的平分线”他这样做的依据是（　　）

A．角平分线上的点到这个角两边的距离相等
B．角的内部到角的两边的距离相等的点在角的平分线上
C．三角形三条角平分线的交点到三条边的距离相等
D．以上均不正确

9．（3分）如图，在平面直角坐标系中，已知点A（2，4），B（4，1），以原点O为位似中心，将△OAB扩大为原来的4倍，则点A的对应点的坐标是（　　）

A．（12，1） B．（−12，﹣1）
C．（8，16）或（﹣16，﹣8） D．（8，16）或（﹣8，﹣16）
10．（3分）《九章算术》是我国古代数学名著，有题译文如下：今有门，不知其高宽；有竿，不知其长短．横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线长恰好相等．问门高、宽和对角线的长各是多少？设门对角线的长为x尺，下列方程符合题意的是（　　）
A．（x+2）2+（x﹣4）2＝x2 B．（x﹣2）2+（x﹣4）2＝x2
C．x2+（x﹣2）2＝（x﹣4）2 D．（x﹣2）2+x2＝（x+4）2
二、填空题（本大题共有6小题，每小题3分，共18分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）
11．（3分）因式分解：m2+2m＝　 　．
12．（3分）一个口袋中有红球、白球共10个，这些球除颜色外都相同．将口袋中的球搅拌均匀，从中随机摸出一个球，记下颜色后再放回口袋中．不断重复这一过程，共摸了100次球，发现有70次摸到红球．请你估计这个口袋中红球的数量是 　 　．
13．（3分）已知m是方程x2﹣2x﹣1＝0的一个根，则代数式2m2﹣4m+2020的值为 　 　．
14．（3分）已知锐角∠AOB＝40°，如图，按下列步骤作图：
①在OA边取一点D，以O为圆心，OD长为半径画MN，交OB于点C，连接CD．
②以D为圆心，DO长为半径画GH，交OB于点E，连接DE．则∠CDE的度数为 　 　．

15．（3分）一块直角边分别为6cm和8cm的三角木板，绕6cm的边旋转一周，则斜边扫过的面积是　 　cm2（结果用含π的式子表示）．

16．（3分）在直角坐标系中，等边△AOB如图放置，点A的坐标为（1，0），每一次将△AOB绕着点O逆时针方向旋转60°，同时每边扩大为原来的2倍，第一次旋转后得到△A1OB1；第二次旋转后得到△A2OB2，…，以此类推，则点A2022的坐标为 　 　．

三、解答题（本大题共有9小题，共72分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）
17．（6分）计算：(−1)2022+8−4sin45°−|−2|．



18．（6分）解不等式组：x−3＜43x+24≥1．

19．（6分）长沙电视塔位于长沙市岳麓区岳麓山峰顶，其功能集广播电视信号发射与旅游观光于一身，登塔可鸟瞰长沙全貌．为测量电视塔的高度，数学综合实践小组同学先在电视塔附近一栋楼房的底端A点处观测电视塔顶端C处的仰角是60°，然后在安全人员的引导下去该楼房顶端B点处观测电视塔底部D处的俯角是30°．已知楼房高AB约是24m．（结果用根号表示）
（1）求楼房与电视塔底部距离AD的长；
（2）求电视塔的高度．




20．（8分）为贯彻全民健身国家战略、实施健康中国行动，长沙市设立了多个智慧社区健身中心，相比于传统商业健身房，智慧社区健身中心有距离近、价格优惠、场馆智能等优势．为了解消费者对于身边智慧社区健身中心的满意程度，随机抽取若干名到智慧社区健身中心的消费者进行调研，根据调研情况制作了如下不完整的条形统计图和扇形统计图：

（1）此次随机调研了 　 　人，并将条形统计图补充完整；
（2）在扇形统计图中，满意程度为“非常满意”所占百分比为 　 　，满意程度为“基本满意”所对应的扇形圆心角的度数为 　 　；
（3）若目前到智慧社区健身中心健身的人有600人，请你估计对于智慧社区健身中心持满意观点（满意及以上）的人数．







21．（8分）直线y＝﹣x+5与x轴交于点A，与y轴交于点B，抛物线y＝﹣x2+bx+c经过A、B两点，顶点为P．
（1）求抛物线的解析式；
（2）求△ABP的面积．

22．（9分）某物流公司承接A、B两种货物运输业务，已知5月份A货物运费单价为50元/吨，B货物运费单价为30元/吨，共收取运费9500元；6月份由于油价上涨，运费单价上涨为：A货物70元/吨，B货物40元/吨；该物流公司6月承接的A种货物和B种数量与5月份相同，6月份共收取运费13000元．
（1）该物流公司5月份运输两种货物各多少吨？
（2）该物流公司预计7月份运输这两种货物330吨，且A货物的数量不大于B货物的2倍，在运费单价与6月份相同的情况下，该物流公司7月份最多将收到多少运输费？

23．（9分）如图，四边形ABCD中，AD∥BC，∠A＝∠D＝90°，点E是AD的中点，连接BE，将△ABE沿BE折叠后得到△GBE，且点G在四边形ABCD内部，延长BG交DC于点F，连接EF．
（1）求证：四边形ABCD是矩形；
（2）求证：GF＝DF；
（3）若点AB＝6，BC＝8，求DF的长．


24．（10分）在y关于x的函数中，对于实数a，b（b＞a），当a≤x≤b时，函数y有最大值ymax，满足ymax＝2（b﹣a），则称函数为“倍增函数”．
（1）当a＝1，b＝3时，判断下列函数是否为“倍增函数”？如果是，请在对应_____内画“√”，如果不是，请在对应_____内画“×”；
①y＝2x　 　；
②y＝﹣2x+2 　 　；
③y=12x+52　 　．
（2）当b＝2a+1时，反比例函数y=8ax为“倍增函数”，求实数a的值；
（3）已知二次函数y＝x2﹣bx+a2+2a﹣1是“倍增函数”，且y有最大值4，求实数a的值．

25．（10分）如图，BC为⊙O的一条弦，D为弦BC所对的劣弧的中点，A为弦BC所对的优弧上的点，连接AD交BC于点E；
（1）如图1，过D作⊙O的切线MN，求证：MN∥BC；
（2）如图2，若BC为⊙O的直径，连接AB，AC，DB；
①求证：DB2＝DE•DA；
②若DE＝9，AE＝7，点F为△ABC的内心，求OF的长．


2022年湖南省长沙市长郡教育集团中考数学一模试卷
参考答案与试题解析
一、选择题（在下列各题的四个选项中，只有一项是符合题意的．请在答题卡中填涂符合题意的选项．本大题共10个小题，每小题3分，共30分）
1．（3分）下列四个数中，最小的数是（　　）
A．0 B．−12022 C．2022 D．﹣2022
【解答】解：∵|−12022|=12022，|﹣2022|＝2022，而12022＜2022，
∴−2022＜−12022＜0＜2022，
∴最小的数是﹣2022．
故选：D．
2．（3分）下面四个化学仪器示意图中，是轴对称图形的是（　　）
A． B． C． D．
【解答】解：A、不是轴对称图形，故本选项不合题意；
B、不是轴对称图形，故本选项不合题意；
C、不是轴对称图形，故本选项不合题意；
D、是轴对称图形，故本选项符合题意．
故选：D．
3．（3分）2021年9月20日“天舟三号”在海南成功发射，这是中国航天工程又一重大突破，它的运行轨道距离地球393000米，数据393000米用科学记数法表示为（　　）
A．0.393×107米 B．3.93×106米
C．3.93×105米 D．39.3×104米
【解答】解：393000米＝3.93×105米．
故选：C．
4．（3分）如图所示正三棱柱的主视图是（　　）

A． B． C． D．
【解答】解：如图所示正三棱柱的主视图是平行排列的两个矩形，
故选：B．
5．（3分）如图，点D，E分别在∠ABC的边BA，BC上，DE⊥AB，过BA上的点F（位于点D上方作FG∥BC，若∠AFG＝42°，则∠DEB的度数为（　　）

A．42° B．48° C．52° D．58°
【解答】解：∵FG∥BC，∠AFG＝42°，
∴∠DBE＝∠AFG＝42°，
∵DE⊥AB，
∴∠BDE＝90°，
∴∠DEB＝180°﹣∠DBE﹣∠BDE
＝180°﹣42°﹣90°
＝48°．
故选：B．
6．（3分）一次函数y＝﹣x﹣2的图象经过（　　）
A．第一、二、三象限 B．第一、二、四象限
C．第一、三、四象限 D．第二、三、四象限
【解答】解：∵﹣1＜0，
∴一次函数y＝﹣x﹣2的图象一定经过第二、四象限；
又∵﹣2＜0，
∴一次函数y＝﹣x﹣2的图象与y轴交于负半轴，
∴一次函数y＝﹣x﹣2的图象经过第二、三、四象限；
故选：D．
7．（3分）为了落实“作业、睡眠、手机、读物、体质”等五项管理要求，了解学生的睡眠状况，调查了一个班50名学生每天的睡眠时间，绘成睡眠时间频数分布直方图如图所示，则所调查学生睡眠时间的众数，中位数分别为（　　）

A．7h 7h B．8h 7.5h C．7h 7.5h D．8h 8h
【解答】解：∵7h出现了19次，出现的次数最多，
∴所调查学生睡眠时间的众数是7h；
∵共有50名学生，中位数是第25、26个数的平均数，
∴所调查学生睡眠时间的中位数是7+82=7.5（h）．
故选：C．
8．（3分）小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线，另一把直尺压住射线并且与第一把直尺交于点，小明说：“射线就是角的平分线”他这样做的依据是（　　）

A．角平分线上的点到这个角两边的距离相等
B．角的内部到角的两边的距离相等的点在角的平分线上
C．三角形三条角平分线的交点到三条边的距离相等
D．以上均不正确
【解答】解：如图所示：过两把直尺的交点P作PE⊥AO，PF⊥BO，

∵两把完全相同的长方形直尺，
∴PE＝PF，
∴OP平分∠AOB（角的内部到角的两边的距离相等的点在这个角的平分线上），
故选：B．
9．（3分）如图，在平面直角坐标系中，已知点A（2，4），B（4，1），以原点O为位似中心，将△OAB扩大为原来的4倍，则点A的对应点的坐标是（　　）

A．（12，1） B．（−12，﹣1）
C．（8，16）或（﹣16，﹣8） D．（8，16）或（﹣8，﹣16）
【解答】解：∵点A（2，4），B（4，1），以原点O为位似中心，将△OAB扩大为原来的4倍，
∴点A的对应点的坐标是：（8，16）或（﹣8，﹣16）．
故选：D．
10．（3分）《九章算术》是我国古代数学名著，有题译文如下：今有门，不知其高宽；有竿，不知其长短．横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线长恰好相等．问门高、宽和对角线的长各是多少？设门对角线的长为x尺，下列方程符合题意的是（　　）
A．（x+2）2+（x﹣4）2＝x2 B．（x﹣2）2+（x﹣4）2＝x2
C．x2+（x﹣2）2＝（x﹣4）2 D．（x﹣2）2+x2＝（x+4）2
【解答】解：设门对角线的长为x尺，由题意得：
（x﹣2）2+（x﹣4）2＝x2，
故选：B．
二、填空题（本大题共有6小题，每小题3分，共18分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）
11．（3分）因式分解：m2+2m＝　m（m+2）　．
【解答】解：m2+2m＝m（m+2）．
故答案为：m（m+2）．
12．（3分）一个口袋中有红球、白球共10个，这些球除颜色外都相同．将口袋中的球搅拌均匀，从中随机摸出一个球，记下颜色后再放回口袋中．不断重复这一过程，共摸了100次球，发现有70次摸到红球．请你估计这个口袋中红球的数量是 　7　．
【解答】解：由题意可得，
红球的概率为70100=70%，
则这个口袋中红球的个数：10×70%＝7（个）．
故答案为：7．
13．（3分）已知m是方程x2﹣2x﹣1＝0的一个根，则代数式2m2﹣4m+2020的值为 　2022　．
【解答】解：∵m是方程x2﹣2x﹣1＝0的一个根，
∴m2﹣2m﹣1＝0，
∴m2﹣2m＝1，
∴2m2﹣4m+2020＝2（m2﹣2m）+2020＝2+2020＝2022．
故答案为：2022．
14．（3分）已知锐角∠AOB＝40°，如图，按下列步骤作图：
①在OA边取一点D，以O为圆心，OD长为半径画MN，交OB于点C，连接CD．
②以D为圆心，DO长为半径画GH，交OB于点E，连接DE．则∠CDE的度数为 　30°　．

【解答】解：由作法得OD＝OC，DO＝DE，
∵DO＝DE，
∴∠DEO＝∠DOE＝40°，
∴∠ODE＝180°﹣∠DOE﹣∠DEO＝180°﹣40°﹣40°＝100°，
∵OD＝OC，
∴∠ODC＝∠OCD=12（180°﹣∠DOC）=12×（180°﹣40°）＝70°，
∴∠CDE＝∠ODE﹣∠ODC＝100°﹣70°＝30°．
故答案为：30°．
15．（3分）一块直角边分别为6cm和8cm的三角木板，绕6cm的边旋转一周，则斜边扫过的面积是　80π　cm2（结果用含π的式子表示）．

【解答】解：∵一块直角边分别为6cm和8cm的三角木板，绕6cm的边旋转一周，
∴斜边扫过的面积是底面半径为8cm，母线长为AB=62+82=10cm的圆锥，
∴S＝πrl＝π×10×8＝80π，
故答案为：80π．

16．（3分）在直角坐标系中，等边△AOB如图放置，点A的坐标为（1，0），每一次将△AOB绕着点O逆时针方向旋转60°，同时每边扩大为原来的2倍，第一次旋转后得到△A1OB1；第二次旋转后得到△A2OB2，…，以此类推，则点A2022的坐标为 　（22022，0）　．

【解答】解：（1）∵A点坐标为（1，0），
∴OA＝1，
∴第一次旋转后，点A1在第一象限，OA1＝2；
第二次旋转后，点A2在第二象限，OA2=22；
第三次旋转后，点A3在x轴负半轴，OA3＝23；
第四次旋转后，点A4在第三象限，OA4=24；
第五次旋转后，点A5在第四象限，OA5=25；
第六次旋转后，点A6在x轴正半轴，OA6=26；
如此循环，每旋转6次，A的对应点又回到x轴正半轴上，
∵2022÷6＝337，
∴循环了337次，点A2022在x轴正半轴上，且OA2022=22022，
∴A2022(22022，0)．
三、解答题（本大题共有9小题，共72分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）
17．（6分）计算：(−1)2022+8−4sin45°−|−2|．
【解答】解：原式＝1+22−4×22−2
＝1+22−22−2
＝﹣1．
18．（6分）解不等式组：x−3＜43x+24≥1．
【解答】解：解不等式x﹣3＜4，得：x＜7，
解不等式3x+24≥1，得：x≥23，
∴不等式组的解集为23≤x＜7．
19．（6分）长沙电视塔位于长沙市岳麓区岳麓山峰顶，其功能集广播电视信号发射与旅游观光于一身，登塔可鸟瞰长沙全貌．为测量电视塔的高度，数学综合实践小组同学先在电视塔附近一栋楼房的底端A点处观测电视塔顶端C处的仰角是60°，然后在安全人员的引导下去该楼房顶端B点处观测电视塔底部D处的俯角是30°．已知楼房高AB约是24m．（结果用根号表示）
（1）求楼房与电视塔底部距离AD的长；
（2）求电视塔的高度．

【解答】解：（1）∵顶端B点处观测电视塔底部D处的俯角是30°，
∴∠ADB＝30°，
在Rt△ABD中，AB＝24m，
∵tan∠ADB=ABAD=tan30°=33，
∴AD=3AB＝243（m），
答：楼房与电视塔底部距离AD的长为243m；
（2）∵在一楼房的底端A点处观测电视塔顶端C处的仰角是60°，
∴∠CAD＝60°，
在Rt△ACD中，tan∠CAD=CDAD=tan60°=3，
∴CD=3AD=3×243=72（m）．
答：电视塔的高度为72m．
20．（8分）为贯彻全民健身国家战略、实施健康中国行动，长沙市设立了多个智慧社区健身中心，相比于传统商业健身房，智慧社区健身中心有距离近、价格优惠、场馆智能等优势．为了解消费者对于身边智慧社区健身中心的满意程度，随机抽取若干名到智慧社区健身中心的消费者进行调研，根据调研情况制作了如下不完整的条形统计图和扇形统计图：

（1）此次随机调研了 　200　人，并将条形统计图补充完整；
（2）在扇形统计图中，满意程度为“非常满意”所占百分比为 　30%　，满意程度为“基本满意”所对应的扇形圆心角的度数为 　108°　；
（3）若目前到智慧社区健身中心健身的人有600人，请你估计对于智慧社区健身中心持满意观点（满意及以上）的人数．
【解答】解：（1）此次随机调研了：80÷40%＝200（人），
“非常满意”的人数为：200﹣80﹣20﹣40＝60（人），
将条形统计图补充完整如下：

故答案为：200；
（2）在扇形统计图中，满意程度为“非常满意”所占百分比为：60200×100%=30%，满意程度为“基本满意”所对应的扇形圆心角的度数为：360°×30%＝108°，
故答案为：30%；108°；
（3）600×（30%+40%）＝420（人），
答：估计对于智慧社区健身中心持满意观点（满意及以上）的人数为420人．
21．（8分）直线y＝﹣x+5与x轴交于点A，与y轴交于点B，抛物线y＝﹣x2+bx+c经过A、B两点，顶点为P．
（1）求抛物线的解析式；
（2）求△ABP的面积．
【解答】解：（1）∵直线y＝﹣x+5，当y＝0时，由﹣x+5＝0，得x＝5；当x＝0时，y＝5，
∴A（5，0）、B（0，5），
将A（5，0）、B（0，5）代入y＝﹣x2+bx+c，得−25+5b+c=0c=5，解得b=4c=5，
∴抛物线的解析式为y＝﹣x2+4x+5．
（2）∵y＝﹣x2+4x+5＝﹣（x﹣2）2+9，
∴抛物线的顶点P为（2，9），如图，
设AB交对称轴于C，则C（2，3），
∴PC＝9﹣3＝6，
∴S△PAB＝S△PAC+S△PBC=12×3×5=152．

22．（9分）某物流公司承接A、B两种货物运输业务，已知5月份A货物运费单价为50元/吨，B货物运费单价为30元/吨，共收取运费9500元；6月份由于油价上涨，运费单价上涨为：A货物70元/吨，B货物40元/吨；该物流公司6月承接的A种货物和B种数量与5月份相同，6月份共收取运费13000元．
（1）该物流公司5月份运输两种货物各多少吨？
（2）该物流公司预计7月份运输这两种货物330吨，且A货物的数量不大于B货物的2倍，在运费单价与6月份相同的情况下，该物流公司7月份最多将收到多少运输费？
【解答】解：（1）设A种货物运输了x吨，设B种货物运输了y吨，
依题意得：50x+30y=950070x+40y=13000，
解之得：x=100y=150．
答：物流公司5月运输A种货物100吨，B种货物150吨．
（2）设A种货物为a吨，则B种货物为（330﹣a）吨，
依题意得：a≤（330﹣a）×2，
解得：a≤220，
设获得的运输费为W元，则W＝70a+40（330﹣a）＝30a+13200，
根据一次函数的性质，可知W随着a的增大而增大
当W取最大值时a＝220，
即W＝19800元．
所以该物流公司7月份最多将收到19800元运输费．
23．（9分）如图，四边形ABCD中，AD∥BC，∠A＝∠D＝90°，点E是AD的中点，连接BE，将△ABE沿BE折叠后得到△GBE，且点G在四边形ABCD内部，延长BG交DC于点F，连接EF．
（1）求证：四边形ABCD是矩形；
（2）求证：GF＝DF；
（3）若点AB＝6，BC＝8，求DF的长．

【解答】（1）证明：∵AD∥BC，∠A＝∠D＝90°，
∴∠ABC+∠A＝180°，
∴∠ABC＝90°，
∴∠ABC＝∠A＝∠D＝90°，
∴四边形ABCD是矩形；
（2）证明：∵将△ABE沿BE折叠后得到△GBE，
∴△ABE≌△GBE，
∴∠BGE＝∠A，AE＝GE，
∵∠A＝∠D＝90°，
∴∠EGF＝∠D＝90°，
∵EA＝ED，
∴EG＝ED，
在Rt△EGF和Rt△EDF中，
EF=EFEG=ED，
∴Rt△EGF≌Rt△EDF（HL），
∴GF＝DF；
（3）解：由折叠可知AB＝GB，
由（2）知Rt△EGF≌Rt△EDF，
∴GF＝DF，
∵∠C＝90°，AB＝CD＝BG＝6，BC＝8，
∴FC＝DC﹣DF＝6﹣DF，BF＝GF+GF＝6+DF，
∵BF2＝BC2+CF2，
∴（6+DF）2＝64+（6﹣DF）2，
解得DF=83．
24．（10分）在y关于x的函数中，对于实数a，b（b＞a），当a≤x≤b时，函数y有最大值ymax，满足ymax＝2（b﹣a），则称函数为“倍增函数”．
（1）当a＝1，b＝3时，判断下列函数是否为“倍增函数”？如果是，请在对应_____内画“√”，如果不是，请在对应_____内画“×”；
①y＝2x　×　；
②y＝﹣2x+2 　×　；
③y=12x+52　√　．
（2）当b＝2a+1时，反比例函数y=8ax为“倍增函数”，求实数a的值；
（3）已知二次函数y＝x2﹣bx+a2+2a﹣1是“倍增函数”，且y有最大值4，求实数a的值．
【解答】解：（1）∵a＝1，b＝3，
∴ymax＝2（b﹣a）＝4，
①当1≤x≤3时，对y＝2x，当x＝3时函数有最大值6，
∴y＝2x 不是“倍增函数”；
②当1≤x≤3时，对y＝﹣2x+2，当x＝1时函数有最大值0，
∴y＝﹣2x+2不是“倍增函数”；
③当1≤x≤3时，对y=12x+52，当x＝3时函数有最大值4，
∴y=12x+52 是“倍增函数”；
故答案为：×，×，√；
（2）∵b＝2a+1，
∴ymax＝2（b﹣a）＝2a+2，
∵反比例函数y=8ax为“倍增函数”，
∴当a≤x≤b时，函数y有最大值2a+2，
当a＞0时，对函数y=8ax，当x＝a时函数有最大值8，
∴2a+2＝8，
∴a＝3；
当a＜0时，对函数y=8ax，当x＝b时函数有最大值8ab=8a2a+1，
∴8a2a+1=2a+2，
∴8a2+2a+1＝0，
∵Δ＜0，
∴a无解；
综上所述：a＝3；
（3）∵ymax＝2（b﹣a），y有最大值4，
∴b﹣a＝2，
∵二次函数y＝x2﹣bx+a2+2a﹣1是“倍增函数”，
当x＝a时，函数有最大值为a2﹣ba+a2+2a﹣1，
∴a2﹣ba+a2+2a﹣1＝4，
∴a2＝5，
解得a=5或a=−5；
当x＝b时，函数有最大值为b2﹣b2+a2+2a﹣1＝a2+2a﹣1，
∴a2+2a﹣1＝4，
解得a=6−1或a=−6−1；
综上所述：a的值为5或−5或6−1或−6−1．
25．（10分）如图，BC为⊙O的一条弦，D为弦BC所对的劣弧的中点，A为弦BC所对的优弧上的点，连接AD交BC于点E；

（1）如图1，过D作⊙O的切线MN，求证：MN∥BC；
（2）如图2，若BC为⊙O的直径，连接AB，AC，DB；
①求证：DB2＝DE•DA；
②若DE＝9，AE＝7，点F为△ABC的内心，求OF的长．

【解答】解：（1）连接OD，交BC于点P，

∵D为弧BC的中点，
∴OD⊥BC，
∵MN与⊙O相切，
∴OD⊥MN，
∴BC∥MN．
（2）①∵BD=CD，
∴∠DBC＝∠BAD，
∴△DBE∽△DAB，
∴DEDB=DBDA，
∴DB2＝DE•DA．
②∵DE＝9，AE＝7，
由①可得：BD=DE⋅DA=12，
∴BC=2BD=122，
∴BO＝CO=62，
设CE＝x，则BE=122−x，
∵∠D＝∠C，∠BED＝∠AEC，
∴△BED∽△AEC，
∴AEBE=CEDE
∴BE•CE＝AE•DE，
∴x•（122−x）＝7×9，
解得：x=62−3或x=62+3（舍），
∵△BED∽△AEC，
∴CEDE=ACBD，
∴AC=CE⋅BDDE=82−4，
∴AB=BC2−AC2=82+4，
如图，将△ABC单独分析，过点F作FG⊥AB于点G，作FQ⊥AC于点Q，作FP⊥BC于点P，

∵F为内心，
∴FG＝FQ＝FP=2S△ABCC△ABC=AB⋅ACAB+AC+BC=(82+4)(82−4)82+4+82−4+122=22，
∵∠CAE＝45°，
∴AQ＝FQ=22，
∴CP＝CQ＝AC﹣AQ=62−4，
∴OP＝OC﹣CP＝4，
∴OF=OP2+FP2=26．