江苏省淮安市五年（2017-2021）中考数学真题分类汇编

这是一份江苏省淮安市五年（2017-2021）中考数学真题分类汇编，文件包含06解答题提升题知识点分类-江苏省淮安市五年2017-2021中考数学真题分类汇编含答案17题docx、05解答题中档题知识点分类-江苏省淮安市五年2017-2021中考数学真题分类汇编含答案23题docx、01选择题知识点分类-江苏省淮安市五年2017-2021中考数学真题分类汇编含答案40题docx、02填空题基础题知识点分类-江苏省淮安市五年2017-2021中考数学真题分类汇编含答案30题docx、04解答题基础题知识点分类-江苏省淮安市五年2017-2021中考数学真题分类汇编含答案14题docx、03填空题中档题知识点分类-江苏省淮安市五年2017-2021中考数学真题分类汇编含答案12题docx等6份试卷配套教学资源，其中试卷共125页， 欢迎下载使用。
05解答题（中档题）知识点分类

一．分式的化简求值（共1小题）
1．（2018•淮安）先化简，再求值：（1−1a+1）÷2aa2−1，其中a＝﹣3．
二．解一元一次不等式组（共1小题）
2．（2018•淮安）（1）解不等式组：3x−5＜x+12x−1≥3x−12
三．一元一次不等式组的整数解（共1小题）
3．（2017•淮安）解不等式组：3x−1＜x+5x−32＜x−1并写出它的整数解．
四．一次函数的应用（共2小题）
4．（2020•淮安）甲、乙两地的路程为290千米，一辆汽车早上8：00从甲地出发，匀速向乙地行驶，途中休息一段时间后．按原速继续前进，当离甲地路程为240千米时接到通知，要求中午12：00准时到达乙地．设汽车出发x小时后离甲地的路程为y千米，图中折线OCDE表示接到通知前y与x之间的函数关系．
（1）根据图象可知，休息前汽车行驶的速度为　 　千米/小时；
（2）求线段DE所表示的y与x之间的函数表达式；
（3）接到通知后，汽车仍按原速行驶能否准时到达？请说明理由．

5．（2019•淮安）快车从甲地驶向乙地，慢车从乙地驶向甲地，两车同时出发并且在同一条公路上匀速行驶，途中快车休息1.5小时，慢车没有休息．设慢车行驶的时间为x小时，快车行驶的路程为y1千米，慢车行驶的路程为y2千米．如图中折线OAEC表示y1与x之间的函数关系，线段OD表示y2与x之间的函数关系．
请解答下列问题：
（1）求快车和慢车的速度；
（2）求图中线段EC所表示的y1与x之间的函数表达式；
（3）线段OD与线段EC相交于点F，直接写出点F的坐标，并解释点F的实际意义．

五．二次函数的应用（共2小题）
6．（2021•淮安）某超市经销一种商品，每件成本为50元．经市场调研，当该商品每件的销售价为60元时，每个月可销售300件，若每件的销售价每增加1元，则每个月的销售量将减少10件．设该商品每件的销售价为x元，每个月的销售量为y件．
（1）求y与x的函数表达式；
（2）当该商品每件的销售价为多少元时，每个月的销售利润最大？最大利润是多少？
7．（2018•淮安）某景区商店销售一种纪念品，每件的进货价为40元．经市场调研，当该纪念品每件的销售价为50元时，每天可销售200件；当每件的销售价每增加1元，每天的销售数量将减少10件．
（1）当每件的销售价为52元时，该纪念品每天的销售数量为　 　件；
（2）当每件的销售价x为多少时，销售该纪念品每天获得的利润y最大？并求出最大利润．
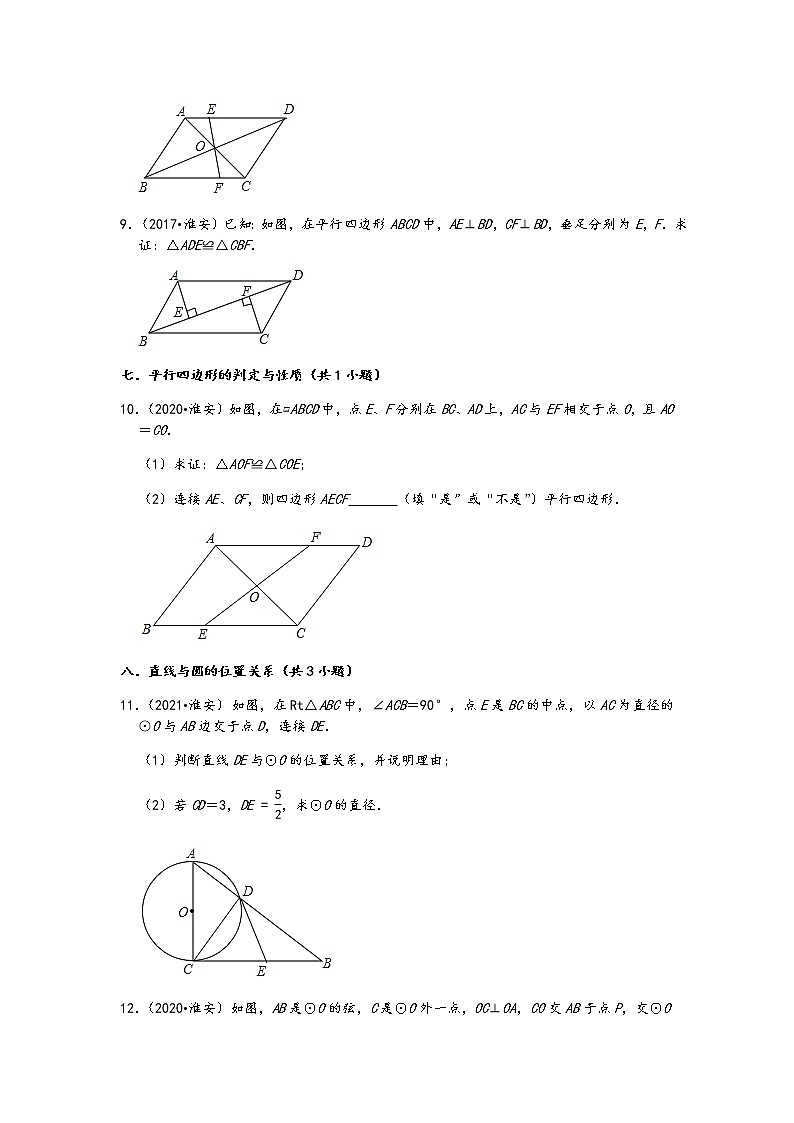
六．平行四边形的性质（共2小题）
8．（2018•淮安）已知：如图，▱ABCD的对角线AC、BD相交于点O，过点O的直线分别与AD、BC相交于点E、F．求证：AE＝CF．

9．（2017•淮安）已知：如图，在平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E，F．求证：△ADE≌△CBF．

七．平行四边形的判定与性质（共1小题）
10．（2020•淮安）如图，在▱ABCD中，点E、F分别在BC、AD上，AC与EF相交于点O，且AO＝CO．
（1）求证：△AOF≌△COE；
（2）连接AE、CF，则四边形AECF　 　（填“是”或“不是”）平行四边形．

八．直线与圆的位置关系（共3小题）
11．（2021•淮安）如图，在Rt△ABC中，∠ACB＝90°，点E是BC的中点，以AC为直径的⊙O与AB边交于点D，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若CD＝3，DE=52，求⊙O的直径．

12．（2020•淮安）如图，AB是⊙O的弦，C是⊙O外一点，OC⊥OA，CO交AB于点P，交⊙O于点D，且CP＝CB．
（1）判断直线BC与⊙O的位置关系，并说明理由；
（2）若∠A＝30°，OP＝1，求图中阴影部分的面积．

13．（2019•淮安）如图，AB是⊙O的直径，AC与⊙O交于点F，弦AD平分∠BAC，DE⊥AC，垂足为E．
（1）试判断直线DE与⊙O的位置关系，并说明理由；
（2）若⊙O的半径为2，∠BAC＝60°，求线段EF的长．

九．作图-旋转变换（共2小题）
14．（2021•淮安）如图，方格纸上每个小正方形的边长均为1个单位长度，△ABC的顶点A、B、C都在格点上（两条网格线的交点叫格点）．请仅用无刻度的直尺按下列要求画图，并保留画图痕迹（不要求写画法）．
（1）将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B1，点C的对应点为C1，画出△AB1C1；
（2）连接CC1，△ACC1的面积为 　 　；
（3）在线段CC1上画一点D，使得△ACD的面积是△ACC1面积的15．

15．（2019•淮安）如图，方格纸上每个小正方形的边长均为1个单位长度，点A、B都在格点上（两条网格线的交点叫格点）．
（1）将线段AB向上平移两个单位长度，点A的对应点为点A1，点B的对应点为点B1，请画出平移后的线段A1B1；
（2）将线段A1B1绕点A1按逆时针方向旋转90°，点B1的对应点为点B2，请画出旋转后的线段A1B2；
（3）连接AB2、BB2，求△ABB2的面积．

一十．解直角三角形的应用-仰角俯角问题（共1小题）
16．（2021•淮安）如图，平地上一幢建筑物AB与铁塔CD相距50m，在建筑物的顶部A处测得铁塔顶部C的仰角为28°、铁塔底部D的俯角为40°，求铁塔CD的高度．
（参考数据：sin28°≈0.47，cos28°≈0.8，tan28°≈0.53，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）

一十一．扇形统计图（共1小题）
17．（2021•淮安）市环保部门为了解城区某一天18：00时噪声污染情况，随机抽取了城区部分噪声测量点这一时刻的测量数据进行统计，把所抽取的测量数据分成A、B、C、D、E五组，并将统计结果绘制了两幅不完整的统计图表．
组别
噪声声级x/dB
频数
A
55≤x＜60
4
B
60≤x＜65
10
C
65≤x＜70
m
D
70≤x＜75
8
E
75≤x＜80
n
请解答下列问题：
（1）m＝　 　，n＝　 　；
（2）在扇形统计图中D组对应的扇形圆心角的度数是 　 　°；
（3）若该市城区共有400个噪声测量点，请估计该市城区这一天18：00时噪声声级低于70dB的测量点的个数．

一十二．条形统计图（共1小题）
18．（2018•淮安）某学校为了解学生上学的交通方式，现从全校学生中随机抽取了部分学生进行“我上学的交通方式”问卷调查，规定每人必须并且只能在“乘车”、“步行”、“骑车”和“其他”四项中选择一项，并将统计结果绘制了如下两幅不完整的统计图．
请解答下列问题：
（1）在这次调查中，该学校一共抽样调查了　 　名学生；
（2）补全条形统计图；
（3）若该学校共有1500名学生，试估计该学校学生中选择“步行”方式的人数．

一十三．列表法与树状图法（共5小题）
19．（2021•淮安）在三张形状、大小、质地均相同的卡片上各写一个数字，分别为1、2、﹣1．现将三张卡片放入一只不透明的盒子中，搅匀后任意抽出一张，记下数字后放回，搅匀后再任意抽出一张记下数字．
（1）第一次抽到写有负数的卡片的概率是 　 　；
（2）用画树状图或列表等方法求两次抽出的卡片上数字都为正数的概率．
20．（2020•淮安）一只不透明的袋子中，装有三个大小、质地都相同的乒乓球，球面上分别标有字母A、O、K．搅匀后先从袋中任意摸出一个球，将对应字母记入图中的左边方格内；然后将球放回袋中搅匀，再从袋中任意摸出一个球，将对应字母记入图中的右边方格内．
（1）第一次摸到字母A的概率为 　 　；
（2）用画树状图或列表等方法求两个方格中的字母从左往右恰好组成“OK”的概率．

21．（2019•淮安）在三张大小、质地均相同的卡片上各写一个数字，分别为5、8、8，现将三张卡片放入一只不透明的盒子中，搅匀后从中任意摸出一张，记下数字后放回，搅匀后再任意摸出一张，记下数字．
（1）用树状图或列表等方法列出所有可能结果；
（2）求两次摸到不同数字的概率．
22．（2018•淮安）一只不透明袋子中装有三只大小、质地都相同的小球，球面上分别标有数字1、﹣2、3，搅匀后先从中任意摸出一个小球（不放回），记下数字作为点A的横坐标，再从余下的两个小球中任意摸出一个小球，记下数字作为点A的纵坐标．
（1）用画树状图或列表等方法列出所有可能出现的结果；
（2）求点A落在第四象限的概率．
23．（2017•淮安）一只不透明的袋子中装有2个白球和1个红球，这些球除颜色外都相同，搅匀后从中任意摸出1个球（不放回），再从余下的2个球中任意摸出1个球．
（1）用树状图或列表等方法列出所有可能出现的结果；
（2）求两次摸到的球的颜色不同的概率．

参考答案与试题解析
一．分式的化简求值（共1小题）
1．（2018•淮安）先化简，再求值：（1−1a+1）÷2aa2−1，其中a＝﹣3．
【解析】解：原式＝（a+1a+1−1a+1）÷2a(a+1)(a−1)
=aa+1•(a+1)(a−1)2a
=a−12，
当a＝﹣3时，
原式=−3−12=−2．
二．解一元一次不等式组（共1小题）
2．（2018•淮安）（1）解不等式组：3x−5＜x+12x−1≥3x−12
【解析】解：（1）解不等式3x﹣5＜x+1，得：x＜3，
解不等式2x﹣1≥3x−12，得：x≥1，
则不等式组的解集为1≤x＜3．
三．一元一次不等式组的整数解（共1小题）
3．（2017•淮安）解不等式组：3x−1＜x+5x−32＜x−1并写出它的整数解．
【解析】解：解不等式3x﹣1＜x+5，得：x＜3，
解不等式x−32＜x﹣1，得：x＞﹣1，
则不等式组的解集为﹣1＜x＜3，
∴不等式组的整数解为0、1、2．
四．一次函数的应用（共2小题）
4．（2020•淮安）甲、乙两地的路程为290千米，一辆汽车早上8：00从甲地出发，匀速向乙地行驶，途中休息一段时间后．按原速继续前进，当离甲地路程为240千米时接到通知，要求中午12：00准时到达乙地．设汽车出发x小时后离甲地的路程为y千米，图中折线OCDE表示接到通知前y与x之间的函数关系．
（1）根据图象可知，休息前汽车行驶的速度为　80　千米/小时；
（2）求线段DE所表示的y与x之间的函数表达式；
（3）接到通知后，汽车仍按原速行驶能否准时到达？请说明理由．

【解析】解：（1）由图象可知，休息前汽车行驶的速度为80千米/小时；
故答案为：80；

（2）休息后按原速继续前进行驶的时间为：（240﹣80）÷80＝2（小时），
∴点E的坐标为（3.5，240），
设线段DE所表示的y与x之间的函数表达式为y＝kx+b，则：
1.5k+b=803.5k+b=240，解得k=80b=−40，
∴线段DE所表示的y与x之间的函数表达式为：y＝80x﹣40（1.5≤x≤3.5）；

（3）接到通知后，汽车仍按原速行驶，则全程所需时间为：290÷80+0.5＝4.125（小时），
12：00﹣8：00＝4（小时），
4.125＞4，
所以接到通知后，汽车仍按原速行驶不能准时到达．
5．（2019•淮安）快车从甲地驶向乙地，慢车从乙地驶向甲地，两车同时出发并且在同一条公路上匀速行驶，途中快车休息1.5小时，慢车没有休息．设慢车行驶的时间为x小时，快车行驶的路程为y1千米，慢车行驶的路程为y2千米．如图中折线OAEC表示y1与x之间的函数关系，线段OD表示y2与x之间的函数关系．
请解答下列问题：
（1）求快车和慢车的速度；
（2）求图中线段EC所表示的y1与x之间的函数表达式；
（3）线段OD与线段EC相交于点F，直接写出点F的坐标，并解释点F的实际意义．

【解析】解：（1）快车的速度为：180÷2＝90千米/小时，
慢车的速度为：180÷3＝60千米/小时，
答：快车的速度为90千米/小时，慢车的速度为60千米/小时；
（2）由题意可得，
点E的横坐标为：2+1.5＝3.5，
则点E的坐标为（3.5，180），
快车从点E到点C用的时间为：（360﹣180）÷90＝2（小时），
则点C的坐标为（5.5，360），
设线段EC所表示的y1与x之间的函数表达式是y1＝kx+b，
3.5k+b=1805.5k+b=360，得k=90b=−135，
即线段EC所表示的y1与x之间的函数表达式是y1＝90x﹣135（3.5≤x≤5.5）；
（3）设点F的横坐标为a，
则60a＝90a﹣135，
解得，a＝4.5，
则60a＝270，
即点F的坐标为（4.5，270），点F代表的实际意义是在4.5小时时，快车与慢车行驶的路程相等．
五．二次函数的应用（共2小题）
6．（2021•淮安）某超市经销一种商品，每件成本为50元．经市场调研，当该商品每件的销售价为60元时，每个月可销售300件，若每件的销售价每增加1元，则每个月的销售量将减少10件．设该商品每件的销售价为x元，每个月的销售量为y件．
（1）求y与x的函数表达式；
（2）当该商品每件的销售价为多少元时，每个月的销售利润最大？最大利润是多少？
【解析】解：（1）根据题意，y＝300﹣10（x﹣60）
∴y与x的函数表达式为：y＝﹣10x+900；

（2）设每个月的销售利润为w，
由（1）知：w＝﹣10x2+1400x﹣45000，
∴w＝﹣10（x﹣70）2+4000，
∴每件销售价为70元时，获得最大利润；最大利润为4000元．
7．（2018•淮安）某景区商店销售一种纪念品，每件的进货价为40元．经市场调研，当该纪念品每件的销售价为50元时，每天可销售200件；当每件的销售价每增加1元，每天的销售数量将减少10件．
（1）当每件的销售价为52元时，该纪念品每天的销售数量为　180　件；
（2）当每件的销售价x为多少时，销售该纪念品每天获得的利润y最大？并求出最大利润．
【解析】解：（1）由题意得：200﹣10×（52﹣50）＝200﹣20＝180（件），
故答案为：180；
（2）由题意得：
y＝（x﹣40）[200﹣10（x﹣50）]
＝﹣10x2+1100x﹣28000
＝﹣10（x﹣55）2+2250
∴每件销售价为55元时，获得最大利润；最大利润为2250元．
六．平行四边形的性质（共2小题）
8．（2018•淮安）已知：如图，▱ABCD的对角线AC、BD相交于点O，过点O的直线分别与AD、BC相交于点E、F．求证：AE＝CF．

【解析】证明：∵▱ABCD的对角线AC，BD交于点O，
∴AO＝CO，AD∥BC，
∴∠EAC＝∠FCO，
在△AOE和△COF中
∠EAO=∠FCOAO=CO∠AOE=∠COF，
∴△AOE≌△COF（ASA），
∴AE＝CF．
9．（2017•淮安）已知：如图，在平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E，F．求证：△ADE≌△CBF．

【解析】证明：∵四边形ABCD是平行四边形，
∴AD＝CB，AD∥BC，
∴∠ADE＝∠CBF，
∵AE⊥BD，CF⊥BD，
∴∠AED＝∠CFB＝90°，
在△ADE和△CBF中，∠ADE=∠CBF∠AED=∠CFBAD=CB，
∴△ADE≌△CBF（AAS）．
七．平行四边形的判定与性质（共1小题）
10．（2020•淮安）如图，在▱ABCD中，点E、F分别在BC、AD上，AC与EF相交于点O，且AO＝CO．
（1）求证：△AOF≌△COE；
（2）连接AE、CF，则四边形AECF　是　（填“是”或“不是”）平行四边形．

【解析】（1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠OAF＝∠OCE，
在△AOF和△COE中，∠OAF=∠OCEAO=CO∠AOF=∠COE，
∴△AOF≌△COE（ASA）
（2）解：四边形AECF是平行四边形，理由如下：
由（1）得：△AOF≌△COE，
∴FO＝EO，
又∵AO＝CO，
∴四边形AECF是平行四边形；
故答案为：是．

八．直线与圆的位置关系（共3小题）
11．（2021•淮安）如图，在Rt△ABC中，∠ACB＝90°，点E是BC的中点，以AC为直径的⊙O与AB边交于点D，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若CD＝3，DE=52，求⊙O的直径．

【解析】（1）证明：连接DO，如图，

∵直径所对圆周角，
∴∠ADC＝90°，
∴∠BDC＝90°，E为BC的中点，
∴DE＝CE＝BE，
∴∠EDC＝∠ECD，
又∵OD＝OC，
∴∠ODC＝∠OCD，
而∠OCD+∠DCE＝∠ACB＝90°，
∴∠EDC+∠ODC＝90°，即∠EDO＝90°，
∴DE⊥OD且OD为半径，
∴DE与⊙O相切；

（2）由（1）得，∠CDB＝90°，
∵CE＝EB，
∴DE=12BC，
∴BC＝5，
∴BD=BC2−CD2=52−32=4，
∵∠BCA＝∠BDC＝90°，∠B＝∠B，
∴△BCA∽△BDC，
∴ACCD=BCBD，
∴AC3=54，
∴AC=154，
∴⊙O直径的长为154．
12．（2020•淮安）如图，AB是⊙O的弦，C是⊙O外一点，OC⊥OA，CO交AB于点P，交⊙O于点D，且CP＝CB．
（1）判断直线BC与⊙O的位置关系，并说明理由；
（2）若∠A＝30°，OP＝1，求图中阴影部分的面积．

【解析】解：（1）CB与⊙O相切，
理由：连接OB，
∵OA＝OB，
∴∠OAB＝∠OBA，
∵CP＝CB，
∴∠CPB＝∠CBP，
∵∠CPB＝∠APO，
∴∠CBP＝∠APO，
在Rt△AOP中，∵∠A+∠APO＝90°，
∴∠OBA+∠CBP＝90°，
即：∠OBC＝90°，
∴OB⊥CB，
又∵OB是半径，
∴CB与⊙O相切；
（2）∵∠A＝30°，∠AOP＝90°，
∴∠APO＝60°，
∴∠BPD＝∠APO＝60°，
∵PC＝CB，
∴△PBC是等边三角形，
∴∠PCB＝∠CBP＝60°，
∴∠OBP＝∠POB＝30°，
∴OP＝PB＝PC＝1，
∴BC＝1，
∴OB=OC2−BC2=3，
∴图中阴影部分的面积＝S△OBC﹣S扇形OBD=12×1×3−30⋅π×(3)2360=32−π4．

13．（2019•淮安）如图，AB是⊙O的直径，AC与⊙O交于点F，弦AD平分∠BAC，DE⊥AC，垂足为E．
（1）试判断直线DE与⊙O的位置关系，并说明理由；
（2）若⊙O的半径为2，∠BAC＝60°，求线段EF的长．

【解析】解：（1）直线DE与⊙O相切，
连接OD．
∵AD平分∠BAC，
∴∠OAD＝∠CAD，
∵OA＝OD，
∴∠OAD＝∠ODA，
∴∠ODA＝∠CAD，
∴OD∥AC，
∵DE⊥AC，即∠AED＝90°，
∴∠ODE＝90°，即DE⊥OD，
∴DE是⊙O的切线；
（2）过O作OG⊥AF于G，
∴AF＝2AG，
∵∠BAC＝60°，OA＝2，
∴AG=12OA＝1，
∴AF＝2，
∴AF＝OD，
∵AE⊥DE，OD⊥DE，
∴AF∥OD，
∴四边形AODF是平行四边形，
∵AF＝AO，
∴四边形AODF是菱形，
∴DF∥OA，DF＝OA＝2，
∴∠EFD＝∠BAC＝60°，
∴EF=12DF＝1．

九．作图-旋转变换（共2小题）
14．（2021•淮安）如图，方格纸上每个小正方形的边长均为1个单位长度，△ABC的顶点A、B、C都在格点上（两条网格线的交点叫格点）．请仅用无刻度的直尺按下列要求画图，并保留画图痕迹（不要求写画法）．
（1）将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B1，点C的对应点为C1，画出△AB1C1；
（2）连接CC1，△ACC1的面积为 　52　；
（3）在线段CC1上画一点D，使得△ACD的面积是△ACC1面积的15．

【解析】解：（1）如图：
图中△AB1C1即为要求所作三角形；

（2）∵AC=12+22=5，由旋转性质知AC＝AC1，∠CAC1＝90°，
∴△ACC1的面积为12×AC×AC1=52，
故答案为：52；

（3）连接EF交CC1于D，即为所求点D，理由如下：
∵CF∥C1E，
∴△CFD∽△C1ED，
∴CDC1D=CFC1E=14，
∴CD=15CC1，
∴△ACD的面积＝△ACC1面积的15．

15．（2019•淮安）如图，方格纸上每个小正方形的边长均为1个单位长度，点A、B都在格点上（两条网格线的交点叫格点）．
（1）将线段AB向上平移两个单位长度，点A的对应点为点A1，点B的对应点为点B1，请画出平移后的线段A1B1；
（2）将线段A1B1绕点A1按逆时针方向旋转90°，点B1的对应点为点B2，请画出旋转后的线段A1B2；
（3）连接AB2、BB2，求△ABB2的面积．

【解析】解：（1）线段A1B1如图所示；

（2）线段A1B2如图所示；

（3）S△ABB2=4×4−12×2×2−12×2×4−12×2×4＝6．

一十．解直角三角形的应用-仰角俯角问题（共1小题）
16．（2021•淮安）如图，平地上一幢建筑物AB与铁塔CD相距50m，在建筑物的顶部A处测得铁塔顶部C的仰角为28°、铁塔底部D的俯角为40°，求铁塔CD的高度．
（参考数据：sin28°≈0.47，cos28°≈0.8，tan28°≈0.53，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）

【解析】解：如图，过A作AE⊥CD，垂足为E．

则AE＝50m，
在Rt△AEC中，CE＝AE•tan28°≈50×0.53＝26.5（m），
在Rt△AED中，DE＝AE•tan40°≈50×0.84＝42（m），
∴CD＝CE+DE≈26.5+42＝68.5（m）．
答：铁塔CD的高度约为68.5m．
一十一．扇形统计图（共1小题）
17．（2021•淮安）市环保部门为了解城区某一天18：00时噪声污染情况，随机抽取了城区部分噪声测量点这一时刻的测量数据进行统计，把所抽取的测量数据分成A、B、C、D、E五组，并将统计结果绘制了两幅不完整的统计图表．
组别
噪声声级x/dB
频数
A
55≤x＜60
4
B
60≤x＜65
10
C
65≤x＜70
m
D
70≤x＜75
8
E
75≤x＜80
n
请解答下列问题：
（1）m＝　12　，n＝　6　；
（2）在扇形统计图中D组对应的扇形圆心角的度数是 　72　°；
（3）若该市城区共有400个噪声测量点，请估计该市城区这一天18：00时噪声声级低于70dB的测量点的个数．

【解析】解：（1）∵样本容量为10÷25%＝40，
∴m＝40×30%＝12，
∴n＝40﹣（4+10+12+8）＝6，
故答案为：12、6；
（2）在扇形统计图中D组对应的扇形圆心角的度数是360°×840=72°，
故答案为：72；
（3）估计该市城区这一天18：00时噪声声级低于70dB的测量点的个数为400×4+10+1240=260（个）．
一十二．条形统计图（共1小题）
18．（2018•淮安）某学校为了解学生上学的交通方式，现从全校学生中随机抽取了部分学生进行“我上学的交通方式”问卷调查，规定每人必须并且只能在“乘车”、“步行”、“骑车”和“其他”四项中选择一项，并将统计结果绘制了如下两幅不完整的统计图．
请解答下列问题：
（1）在这次调查中，该学校一共抽样调查了　50　名学生；
（2）补全条形统计图；
（3）若该学校共有1500名学生，试估计该学校学生中选择“步行”方式的人数．

【解析】解：（1）本次调查中，该学校调查的学生人数为20÷40%＝50人，
故答案为：50；

（2）步行的人数为50﹣（20+10+5）＝15人，
补全图形如下：


（3）估计该学校学生中选择“步行”方式的人数为1500×1550=450人．
一十三．列表法与树状图法（共5小题）
19．（2021•淮安）在三张形状、大小、质地均相同的卡片上各写一个数字，分别为1、2、﹣1．现将三张卡片放入一只不透明的盒子中，搅匀后任意抽出一张，记下数字后放回，搅匀后再任意抽出一张记下数字．
（1）第一次抽到写有负数的卡片的概率是 　13　；
（2）用画树状图或列表等方法求两次抽出的卡片上数字都为正数的概率．
【解析】解：（1）第一次抽到写有负数的卡片的概率是13，
故答案为：13；

（2）画树状图为：

共有9种等可能的结果数，其中两次抽出的卡片上数字都为正数的有4种结果，
所以两次抽出的卡片上数字都为正数的概率为49．
20．（2020•淮安）一只不透明的袋子中，装有三个大小、质地都相同的乒乓球，球面上分别标有字母A、O、K．搅匀后先从袋中任意摸出一个球，将对应字母记入图中的左边方格内；然后将球放回袋中搅匀，再从袋中任意摸出一个球，将对应字母记入图中的右边方格内．
（1）第一次摸到字母A的概率为 　13　；
（2）用画树状图或列表等方法求两个方格中的字母从左往右恰好组成“OK”的概率．

【解析】解：（1）共有3种可能出现的结果，其中是A的只有1种，
∴第1次摸到A的概率为13，
故答案为：13；
（2）用树状图表示所有可能出现的结果如下：

共有9种可能出现的结果，其中从左到右能构成“OK”的只有1种，
∴P（组成OK）=19．
21．（2019•淮安）在三张大小、质地均相同的卡片上各写一个数字，分别为5、8、8，现将三张卡片放入一只不透明的盒子中，搅匀后从中任意摸出一张，记下数字后放回，搅匀后再任意摸出一张，记下数字．
（1）用树状图或列表等方法列出所有可能结果；
（2）求两次摸到不同数字的概率．
【解析】解：（1）画树状图如图所示：
所有结果为：（5，5），（5，8），（5，8），（8，5），（8，8），（8，8），（8，5），（8，8），（8，8）；
（2）共有9种等可能的结果，两次摸到不同数字的结果有4个，
∴两次摸到不同数字的概率为49．

22．（2018•淮安）一只不透明袋子中装有三只大小、质地都相同的小球，球面上分别标有数字1、﹣2、3，搅匀后先从中任意摸出一个小球（不放回），记下数字作为点A的横坐标，再从余下的两个小球中任意摸出一个小球，记下数字作为点A的纵坐标．
（1）用画树状图或列表等方法列出所有可能出现的结果；
（2）求点A落在第四象限的概率．
【解析】解：（1）列表得：

1
﹣2
3
1

（1，﹣2）
（1，3）
2
（﹣2，1）

（﹣2，3）
3
（3，1）
（3，﹣2）

（2）由表可知，共有6种等可能结果，其中点A落在第四象限的有2种结果，
所以点A落在第四象限的概率为26=13．
23．（2017•淮安）一只不透明的袋子中装有2个白球和1个红球，这些球除颜色外都相同，搅匀后从中任意摸出1个球（不放回），再从余下的2个球中任意摸出1个球．
（1）用树状图或列表等方法列出所有可能出现的结果；
（2）求两次摸到的球的颜色不同的概率．
【解析】解：（1）如图：
；

（2）共有6种情况，两次摸到的球的颜色不同的情况有4种，概率为46=23．