江苏省泰州市五年（2017-2021）中考数学真题分类汇编

这是一份江苏省泰州市五年（2017-2021）中考数学真题分类汇编，文件包含06解答题提升题知识点分类-江苏省泰州市五年2017-2021中考数学真题分类汇编含答案16题docx、05解答题中档题知识点分类-江苏省泰州市五年2017-2021中考数学真题分类汇编含答案21题docx、01选择题知识点分类-江苏省泰州市五年2017-2021中考数学真题分类汇编含答案30题docx、03填空题提升题知识点分类-江苏省泰州市五年2017-2021中考数学真题分类汇编含答案19题docx、04解答题基础题知识点分类-江苏省泰州市五年2017-2021中考数学真题分类汇编含答案13题docx、02填空题基础题知识点分类-江苏省泰州市五年2017-2021中考数学真题分类汇编含答案31题docx等6份试卷配套教学资源，其中试卷共109页， 欢迎下载使用。

01选择题知识点分类

一．相反数（共2小题）
1．（2019•泰州）﹣1的相反数是（　　）
A．±1 B．﹣1 C．0 D．1
2．（2018•泰州）﹣（﹣2）等于（　　）
A．﹣2 B．2 C． D．±2
二．倒数（共1小题）
3．（2020•泰州）﹣2的倒数是（　　）
A．2 B． C．﹣2 D．﹣
三．算术平方根（共1小题）
4．（2017•泰州）2的算术平方根是（　　）
A． B． C． D．2
四．代数式求值（共1小题）
5．（2019•泰州）若2a﹣3b＝﹣1，则代数式4a2﹣6ab+3b的值为（　　）
A．﹣1 B．1 C．2 D．3
五．幂的乘方与积的乘方（共1小题）
6．（2017•泰州）下列运算正确的是（　　）
A．a3•a3＝2a6 B．a3+a3＝2a6 C．（a3）2＝a6 D．a6•a2＝a3
六．零指数幂（共1小题）
7．（2021•泰州）（﹣3）0等于（　　）
A．0 B．1 C．3 D．﹣3
七．同类二次根式（共1小题）
8．（2021•泰州）下列各组二次根式中，化简后是同类二次根式的是（　　）
A．与 B．与 C．与 D．与
八．二次根式的混合运算（共2小题）
9．（2020•泰州）下列等式成立的是（　　）
A．3+4＝7 B．＝ C．÷＝2 D．＝3
10．（2018•泰州）下列运算正确的是（　　）
A．+＝ B．＝2 C．•＝ D．÷＝2
九．根的判别式（共1小题）
11．（2018•泰州）已知x1、x2是关于x的方程x2﹣ax﹣2＝0的两根，下列结论一定正确的是（　　）
A．x1≠x2 B．x1+x2＞0 C．x1•x2＞0 D．x1＜0，x2＜0
一十．根与系数的关系（共1小题）
12．（2019•泰州）方程2x2+6x﹣1＝0的两根为x1、x2，则x1+x2等于（　　）
A．﹣6 B．6 C．﹣3 D．3
一十一．一次函数图象上点的坐标特征（共2小题）
13．（2020•泰州）点P（a，b）在函数y＝3x+2的图象上，则代数式6a﹣2b+1的值等于（　　）
A．5 B．3 C．﹣3 D．﹣1
14．（2018•泰州）如图，平面直角坐标系xOy中，点A的坐标为（9，6），AB⊥y轴，垂足为B，点P从原点O出发向x轴正方向运动，同时，点Q从点A出发向点B运动，当点Q到达点B时，点P、Q同时停止运动，若点P与点Q的速度之比为1：2，则下列说法正确的是（　　）

A．线段PQ始终经过点（2，3）
B．线段PQ始终经过点（3，2）
C．线段PQ始终经过点（2，2）
D．线段PQ不可能始终经过某一定点
一十二．反比例函数图象上点的坐标特征（共1小题）
15．（2017•泰州）如图，P为反比例函数y＝（k＞0）在第一象限内图象上的一点，过点P分别作x轴，y轴的垂线交一次函数y＝﹣x﹣4的图象于点A、B．若∠AOB＝135°，则k的值是（　　）

A．2 B．4 C．6 D．8
一十三．展开图折叠成几何体（共1小题）
16．（2020•泰州）把如图所示的纸片沿着虚线折叠，可以得到的几何体是（　　）

A．三棱柱 B．四棱柱 C．三棱锥 D．四棱锥
一十四．两点间的距离（共1小题）
17．（2021•泰州）互不重合的A、B、C三点在同一直线上，已知AC＝2a+1，BC＝a+4，AB＝3a，这三点的位置关系是（　　）
A．点A在B、C两点之间 B．点B在A、C两点之间
C．点C在A、B两点之间 D．无法确定
一十五．三角形的重心（共2小题）
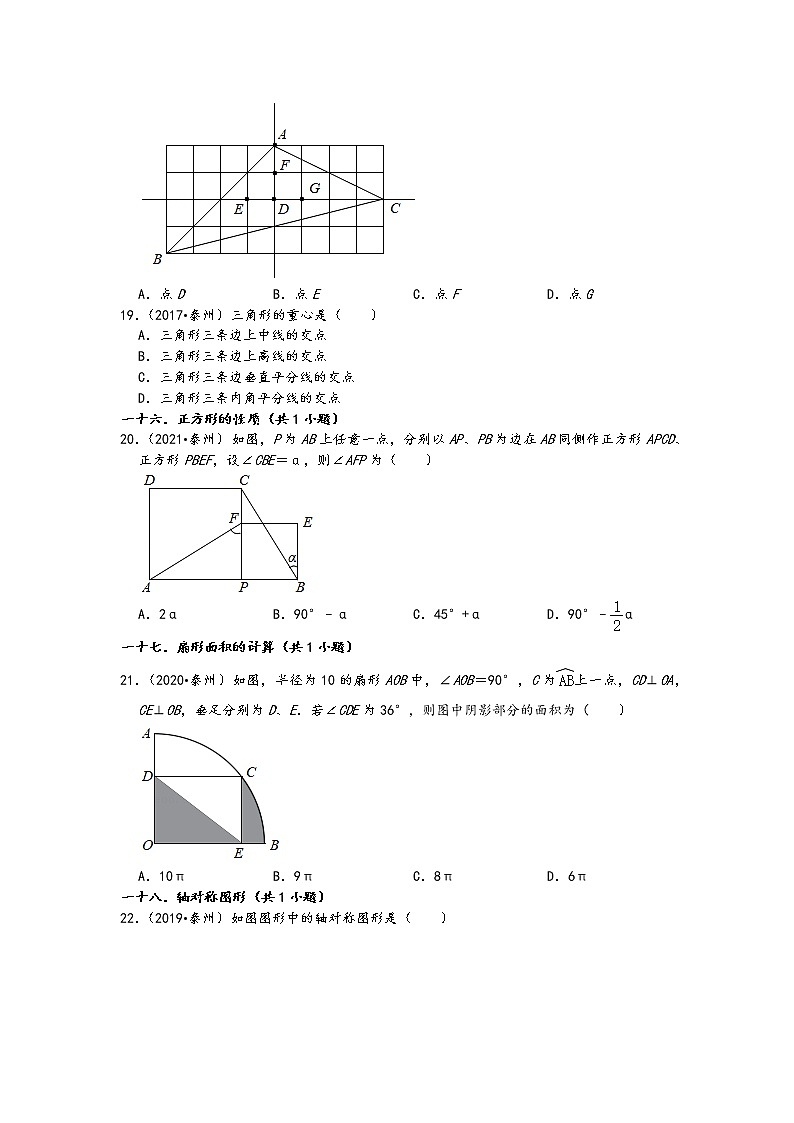
18．（2019•泰州）如图所示的网格由边长相同的小正方形组成，点A、B、C、D、E、F、G在小正方形的顶点上，则△ABC的重心是（　　）

A．点D B．点E C．点F D．点G
19．（2017•泰州）三角形的重心是（　　）
A．三角形三条边上中线的交点
B．三角形三条边上高线的交点
C．三角形三条边垂直平分线的交点
D．三角形三条内角平分线的交点
一十六．正方形的性质（共1小题）
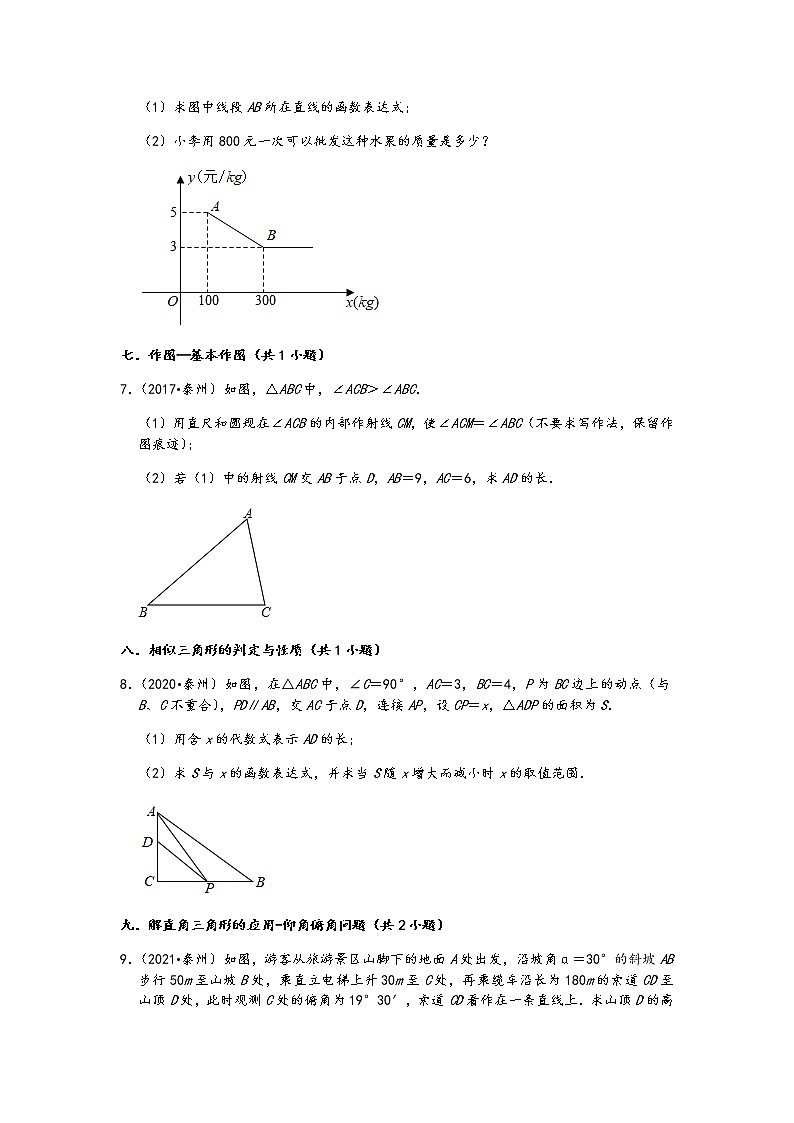
20．（2021•泰州）如图，P为AB上任意一点，分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF，设∠CBE＝α，则∠AFP为（　　）

A．2α B．90°﹣α C．45°+α D．90°﹣α
一十七．扇形面积的计算（共1小题）
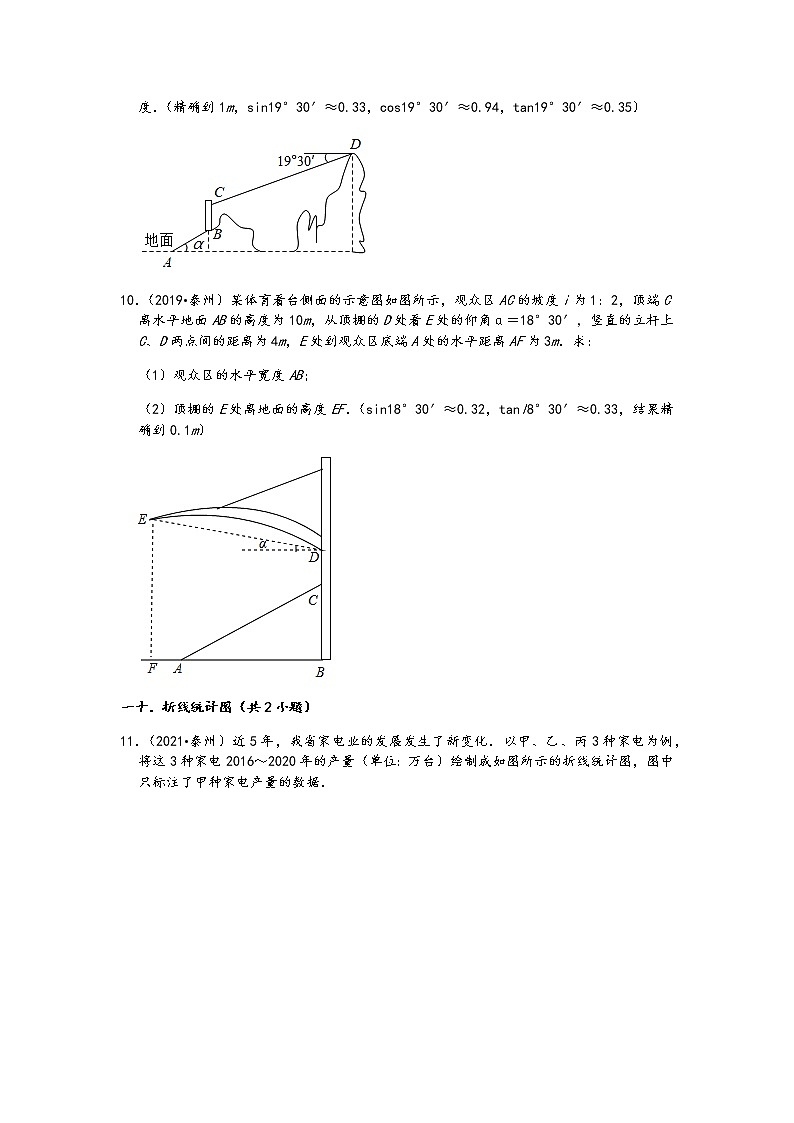
21．（2020•泰州）如图，半径为10的扇形AOB中，∠AOB＝90°，C为上一点，CD⊥OA，CE⊥OB，垂足分别为D、E．若∠CDE为36°，则图中阴影部分的面积为（　　）

A．10π B．9π C．8π D．6π
一十八．轴对称图形（共1小题）
22．（2019•泰州）如图图形中的轴对称图形是（　　）
A． B．
C． D．
一十九．中心对称图形（共1小题）
23．（2017•泰州）把下列英文字母看成图形，既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
二十．简单几何体的三视图（共1小题）
24．（2018•泰州）下列几何体中，主视图与俯视图不相同的是（　　）
A．正方体 B．四棱锥
C．圆柱 D．球
二十一．简单组合体的三视图（共1小题）
25．（2021•泰州）如图所示几何体的左视图是（　　）

A． B．
C． D．
二十二．方差（共1小题）
26．（2017•泰州）某科普小组有5名成员，身高分别为（单位：cm）：160，165，170，163，167．增加1名身高为165cm的成员后，现科普小组成员的身高与原来相比，下列说法正确的是（　　）
A．平均数不变，方差不变 B．平均数不变，方差变大
C．平均数不变，方差变小 D．平均数变小，方差不变
二十三．随机事件（共2小题）
27．（2021•泰州）“14人中至少有2人在同一个月过生日”这一事件发生的概率为P，则（　　）
A．P＝0 B．0＜P＜1 C．P＝1 D．P＞1
28．（2020•泰州）如图，电路图上有4个开关A、B、C、D和1个小灯泡，同时闭合开关A、B或同时闭合开关C、D都可以使小灯泡发光．下列操作中，“小灯泡发光”这个事件是随机事件的是（　　）

A．只闭合1个开关 B．只闭合2个开关
C．只闭合3个开关 D．闭合4个开关
二十四．概率的意义（共1小题）
29．（2018•泰州）小亮是一名职业足球队员，根据以往比赛数据统计，小亮进球率为10%，他明天将参加一场比赛，下面几种说法正确的是（　　）
A．小亮明天的进球率为10%
B．小亮明天每射球10次必进球1次
C．小亮明天有可能进球
D．小亮明天肯定进球
二十五．利用频率估计概率（共1小题）
30．（2019•泰州）小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表：
抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
244
若抛掷硬币的次数为1000，则“正面朝上”的频数最接近（　　）
A．20 B．300 C．500 D．800

参考答案与试题解析
一．相反数（共2小题）
1．（2019•泰州）﹣1的相反数是（　　）
A．±1 B．﹣1 C．0 D．1
【解析】解：﹣1的相反数是：1．
故选：D．
2．（2018•泰州）﹣（﹣2）等于（　　）
A．﹣2 B．2 C． D．±2
【解析】解：﹣（﹣2）＝2，
故选：B．
二．倒数（共1小题）
3．（2020•泰州）﹣2的倒数是（　　）
A．2 B． C．﹣2 D．﹣
【解析】解：﹣2的倒数是﹣．
故选：D．
三．算术平方根（共1小题）
4．（2017•泰州）2的算术平方根是（　　）
A． B． C． D．2
【解析】解：2的算术平方根是，
故选：B．
四．代数式求值（共1小题）
5．（2019•泰州）若2a﹣3b＝﹣1，则代数式4a2﹣6ab+3b的值为（　　）
A．﹣1 B．1 C．2 D．3
【解析】解：4a2﹣6ab+3b，
＝2a（2a﹣3b）+3b，
＝﹣2a+3b，
＝﹣（2a﹣3b），
＝1，
故选：B．
五．幂的乘方与积的乘方（共1小题）
6．（2017•泰州）下列运算正确的是（　　）
A．a3•a3＝2a6 B．a3+a3＝2a6 C．（a3）2＝a6 D．a6•a2＝a3
【解析】解：A、a3•a3＝a6，故此选项错误；
B、a3+a3＝2a3，故此选项错误；
C、（a3）2＝a6，正确；
D、a6•a2＝a8，故此选项错误．
故选：C．
六．零指数幂（共1小题）
7．（2021•泰州）（﹣3）0等于（　　）
A．0 B．1 C．3 D．﹣3
【解析】解：（﹣3）0＝1．
故选：B．
七．同类二次根式（共1小题）
8．（2021•泰州）下列各组二次根式中，化简后是同类二次根式的是（　　）
A．与 B．与 C．与 D．与
【解析】解：A、＝2和不是同类二次根式，本选项不合题意；
B、＝2与不是同类二次根式，本选项不合题意；
C、与不是同类二次根式，本选项不合题意；
D、＝5，＝3是同类二次根式，本选项符合题意．
故选：D．
八．二次根式的混合运算（共2小题）
9．（2020•泰州）下列等式成立的是（　　）
A．3+4＝7 B．＝ C．÷＝2 D．＝3
【解析】解：A．3与4不是同类二次根式，不能合并，此选项计算错误；
B．×＝，此选项计算错误；
C．÷＝×＝3，此选项计算错误；
D．＝3，此选项计算正确；
故选：D．
10．（2018•泰州）下列运算正确的是（　　）
A．+＝ B．＝2 C．•＝ D．÷＝2
【解析】解：A、与不能合并，所以A选项错误；
B、原式＝3，所以B选项错误；
C、原式＝＝，所以C选项错误；
D、原式＝＝2，所以D选项正确．
故选：D．
九．根的判别式（共1小题）
11．（2018•泰州）已知x1、x2是关于x的方程x2﹣ax﹣2＝0的两根，下列结论一定正确的是（　　）
A．x1≠x2 B．x1+x2＞0 C．x1•x2＞0 D．x1＜0，x2＜0
【解析】解：A∵Δ＝（﹣a）2﹣4×1×（﹣2）＝a2+8＞0，
∴x1≠x2，结论A正确；
B、∵x1、x2是关于x的方程x2﹣ax﹣2＝0的两根，
∴x1+x2＝a，
∵a的值不确定，
∴B结论不一定正确；
C、∵x1、x2是关于x的方程x2﹣ax﹣2＝0的两根，
∴x1•x2＝﹣2，结论C错误；
D、∵x1•x2＝﹣2，
∴x1、x2异号，结论D错误．
故选：A．
一十．根与系数的关系（共1小题）
12．（2019•泰州）方程2x2+6x﹣1＝0的两根为x1、x2，则x1+x2等于（　　）
A．﹣6 B．6 C．﹣3 D．3
【解析】解：由于Δ＞0，
∴x1+x2＝﹣3，
故选：C．
一十一．一次函数图象上点的坐标特征（共2小题）
13．（2020•泰州）点P（a，b）在函数y＝3x+2的图象上，则代数式6a﹣2b+1的值等于（　　）
A．5 B．3 C．﹣3 D．﹣1
【解析】解：∵点P（a，b）在函数y＝3x+2的图象上，
∴b＝3a+2，
则3a﹣b＝﹣2．
∴6a﹣2b+1＝2（3a﹣b）+1＝﹣4+1＝﹣3
故选：C．
14．（2018•泰州）如图，平面直角坐标系xOy中，点A的坐标为（9，6），AB⊥y轴，垂足为B，点P从原点O出发向x轴正方向运动，同时，点Q从点A出发向点B运动，当点Q到达点B时，点P、Q同时停止运动，若点P与点Q的速度之比为1：2，则下列说法正确的是（　　）

A．线段PQ始终经过点（2，3）
B．线段PQ始终经过点（3，2）
C．线段PQ始终经过点（2，2）
D．线段PQ不可能始终经过某一定点
【解析】解：当OP＝t时，点P的坐标为（t，0），点Q的坐标为（9﹣2t，6）．
设直线PQ的解析式为y＝kx+b（k≠0），
将P（t，0）、Q（9﹣2t，6）代入y＝kx+b，
，解得：，
∴直线PQ的解析式为y＝x+．
两边乘3﹣t得到：（3﹣t）y＝2x﹣2t，
∴（y﹣2）t＝3y﹣2x，
当y﹣2＝0时，x＝3，
∴直线PQ始终经过（3，2），
故选：B．
一十二．反比例函数图象上点的坐标特征（共1小题）
15．（2017•泰州）如图，P为反比例函数y＝（k＞0）在第一象限内图象上的一点，过点P分别作x轴，y轴的垂线交一次函数y＝﹣x﹣4的图象于点A、B．若∠AOB＝135°，则k的值是（　　）

A．2 B．4 C．6 D．8
【解析】解：方法1、作BF⊥x轴，OE⊥AB，CQ⊥AP，如图1，

设P点坐标（n，），
∵直线AB函数式为y＝﹣x﹣4，PB⊥y轴，PA⊥x轴，
∴C（0，﹣4），G（﹣4，0），
∴OC＝OG，
∴∠OGC＝∠OCG＝45°
∵PB∥OG，PA∥OC，
∴∠PBA＝∠OGC＝45°，∠PAB＝∠OCG＝45°，
∴PA＝PB，
∵P点坐标（n，），
∴OD＝CQ＝n，
∴AD＝AQ+DQ＝n+4；
∵当x＝0时，y＝﹣x﹣4＝﹣4，
∴OC＝DQ＝4，GE＝OE＝OC＝；
同理可证：BG＝BF＝PD＝，
∴BE＝BG+EG＝+；
∵∠AOB＝135°，
∴∠OBE+∠OAE＝45°，
∵∠DAO+∠OAE＝45°，
∴∠DAO＝∠OBE，
∵在△BOE和△AOD中，
，
∴△BOE∽△AOD；
∴＝，即＝；
整理得：nk+2n2＝8n+2n2，化简得：k＝8；
故选D．

方法2、如图2，
过B作BF⊥x轴于F，过点A作AD⊥y轴于D，
∵直线AB函数式为y＝﹣x﹣4，PB⊥y轴，PA⊥x轴，
∴C（0，﹣4），G（﹣4，0），
∴OC＝OG，
∴∠OGC＝∠OCG＝45°
∵PB∥OG，PA∥OC，
∴∠PBA＝∠OGC＝45°，∠PAB＝∠OCG＝45°，
∴PA＝PB，
∵P点坐标（n，），
∴A（n，﹣n﹣4），B（﹣4﹣，）
∵当x＝0时，y＝﹣x﹣4＝﹣4，
∴OC＝4，
当y＝0时，x＝﹣4．
∴OG＝4，
∵∠AOB＝135°，
∴∠BOG+∠AOC＝45°，
∵直线AB的解析式为y＝﹣x﹣4，
∴∠AGO＝∠OCG＝45°，
∴∠BGO＝∠OCA，∠BOG+∠OBG＝45°，
∴∠OBG＝∠AOC，
∴△BOG∽△OAC，
∴＝，
∴＝，
在等腰Rt△BFG中，BG＝BF＝，
在等腰Rt△ACD中，AC＝AD＝n，
∴，
∴k＝8．
故选：D．

一十三．展开图折叠成几何体（共1小题）
16．（2020•泰州）把如图所示的纸片沿着虚线折叠，可以得到的几何体是（　　）

A．三棱柱 B．四棱柱 C．三棱锥 D．四棱锥
【解析】解：观察展开图可知，几何体是三棱柱．
故选：A．
一十四．两点间的距离（共1小题）
17．（2021•泰州）互不重合的A、B、C三点在同一直线上，已知AC＝2a+1，BC＝a+4，AB＝3a，这三点的位置关系是（　　）
A．点A在B、C两点之间 B．点B在A、C两点之间
C．点C在A、B两点之间 D．无法确定
【解析】解：∵AC＝2a+1，BC＝a+4，AB＝3a，A、B、C三点互不重合
∴a＞0，
若点A在B、C之间，
则AB+AC＝BC，
即2a+1+3a＝a+4，
解得a＝，
故A情况存在，
若点B在A、C之间，
则BC+AB＝AC，
即a+4+3a＝2a+1，
解得a＝﹣，
故B情况不存在，
若点C在A、B之间，
则BC+AC＝AB，
即a+4+2a+1＝3a，
此时无解，
故C情况不存在，
∵互不重合的A、B、C三点在同一直线上，
故选：A．
一十五．三角形的重心（共2小题）
18．（2019•泰州）如图所示的网格由边长相同的小正方形组成，点A、B、C、D、E、F、G在小正方形的顶点上，则△ABC的重心是（　　）

A．点D B．点E C．点F D．点G
【解析】解：根据题意可知，直线CD经过△ABC的AB边上的中线，直线AD经过△ABC的BC边上的中线，
∴点D是△ABC重心．
故选：A．
19．（2017•泰州）三角形的重心是（　　）
A．三角形三条边上中线的交点
B．三角形三条边上高线的交点
C．三角形三条边垂直平分线的交点
D．三角形三条内角平分线的交点
【解析】解：三角形的重心是三条中线的交点，
故选：A．
一十六．正方形的性质（共1小题）
20．（2021•泰州）如图，P为AB上任意一点，分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF，设∠CBE＝α，则∠AFP为（　　）

A．2α B．90°﹣α C．45°+α D．90°﹣α
【解析】解：∵四边形PBEF为正方形，
∴∠PBE＝90°，
∵∠CBE＝α，
∴∠PBC＝90°﹣α，
∵四边形APCD、PBEF是正方形，
∴AP＝CP，∠APF＝∠CPB＝90°，PF＝PB，
在△APF和△CPB中，
，
∴△APF≌△CPB（SAS），
∴∠AFP＝∠PBC＝90°﹣α．
故选：B．
一十七．扇形面积的计算（共1小题）
21．（2020•泰州）如图，半径为10的扇形AOB中，∠AOB＝90°，C为上一点，CD⊥OA，CE⊥OB，垂足分别为D、E．若∠CDE为36°，则图中阴影部分的面积为（　　）

A．10π B．9π C．8π D．6π
【解析】解：连接OC，
∵∠AOB＝90°，CD⊥OA，CE⊥OB，
∴四边形CDOE是矩形，
∴CD∥OE，
∴∠DEO＝∠CDE＝36°，
由矩形CDOE易得到△DOE≌△CEO，
∴∠COB＝∠DEO＝36°
∴图中阴影部分的面积＝扇形OBC的面积，
∵S扇形OBC＝＝10π
∴图中阴影部分的面积＝10π，
故选：A．

一十八．轴对称图形（共1小题）
22．（2019•泰州）如图图形中的轴对称图形是（　　）
A． B．
C． D．
【解析】解：A、不是轴对称图形；
B、是轴对称图形；
C、不是轴对称图形；
D、不是轴对称图形；
故选：B．
一十九．中心对称图形（共1小题）
23．（2017•泰州）把下列英文字母看成图形，既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
【解析】解：A、是轴对称图形，不是中心对称图形，故本选项错误；
B、既不是轴对称图形，又不是中心对称图形，故本选项错误；
C、既是轴对称图形又是中心对称图形，故本选项正确；
D、不是轴对称图形，是中心对称图形，故本选项错误．
故选：C．
二十．简单几何体的三视图（共1小题）
24．（2018•泰州）下列几何体中，主视图与俯视图不相同的是（　　）
A．正方体 B．四棱锥
C．圆柱 D．球
【解析】解：四棱锥的主视图与俯视图不同．
故选：B．
二十一．简单组合体的三视图（共1小题）
25．（2021•泰州）如图所示几何体的左视图是（　　）

A． B．
C． D．
【解析】解：从左边看，是一列两个矩形．
故选：C．
二十二．方差（共1小题）
26．（2017•泰州）某科普小组有5名成员，身高分别为（单位：cm）：160，165，170，163，167．增加1名身高为165cm的成员后，现科普小组成员的身高与原来相比，下列说法正确的是（　　）
A．平均数不变，方差不变 B．平均数不变，方差变大
C．平均数不变，方差变小 D．平均数变小，方差不变
【解析】解：＝＝165，S2原＝，
＝＝165，S2新＝，
平均数不变，方差变小，
故选：C．
二十三．随机事件（共2小题）
27．（2021•泰州）“14人中至少有2人在同一个月过生日”这一事件发生的概率为P，则（　　）
A．P＝0 B．0＜P＜1 C．P＝1 D．P＞1
【解析】解：“14人中至少有2人在同一个月过生日”这一事件为必然事件，
∴“14人中至少有2人在同一个月过生日”这一事件发生的概率为P＝1，
故选：C．
28．（2020•泰州）如图，电路图上有4个开关A、B、C、D和1个小灯泡，同时闭合开关A、B或同时闭合开关C、D都可以使小灯泡发光．下列操作中，“小灯泡发光”这个事件是随机事件的是（　　）

A．只闭合1个开关 B．只闭合2个开关
C．只闭合3个开关 D．闭合4个开关
【解析】解：A、只闭合1个开关，小灯泡不会发光，属于不可能事件，不符合题意；
B、只闭合2个开关，小灯泡可能发光也可能不发光，是随机事件，符合题意；
C、只闭合3个开关，小灯泡一定会发光，是必然事件，不符合题意；
D、闭合4个开关，小灯泡一定会发光，是必然事件，不符合题意；
故选：B．
二十四．概率的意义（共1小题）
29．（2018•泰州）小亮是一名职业足球队员，根据以往比赛数据统计，小亮进球率为10%，他明天将参加一场比赛，下面几种说法正确的是（　　）
A．小亮明天的进球率为10%
B．小亮明天每射球10次必进球1次
C．小亮明天有可能进球
D．小亮明天肯定进球
【解析】解：根据以往比赛数据统计，小亮进球率为10%，他明天将参加一场比赛小亮明天有可能进球．
故选：C．
二十五．利用频率估计概率（共1小题）
30．（2019•泰州）小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表：
抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
244
若抛掷硬币的次数为1000，则“正面朝上”的频数最接近（　　）
A．20 B．300 C．500 D．800
【解析】解：观察表格发现：随着试验次数的增加，正面朝上的频率逐渐稳定到0.5附近，
所以抛掷硬币的次数为1000，则“正面朝上”的频数最接近1000×0.5＝500次，
故选：C．