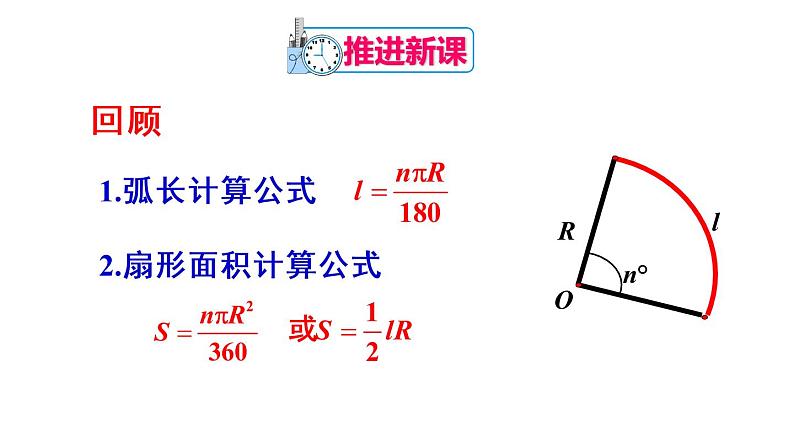
2021学年24.4 弧长及扇形的面积课文内容课件ppt

这是一份2021学年24.4 弧长及扇形的面积课文内容课件ppt，共26页。PPT课件主要包含了弧长计算公式，扇形面积计算公式，圆锥的相关概念，圆锥的侧面积，公式一，公式二，圆锥的全面积，基础巩固，综合应用，拓展延伸等内容，欢迎下载使用。
元旦将近，某家商店正在制作元旦的圆锥形纸帽.如图，已知纸帽的底面周长为58cm，高为20cm，要制作20顶这样的纸帽至少要用多少平方厘米的纸？(结果精确到0.1cm2)
(1)知道什么是圆锥的母线，知道圆锥的侧面展开图是扇形.(2)知道圆锥的侧面积和全面积的计算方法，会求圆锥的侧面积与全面积.
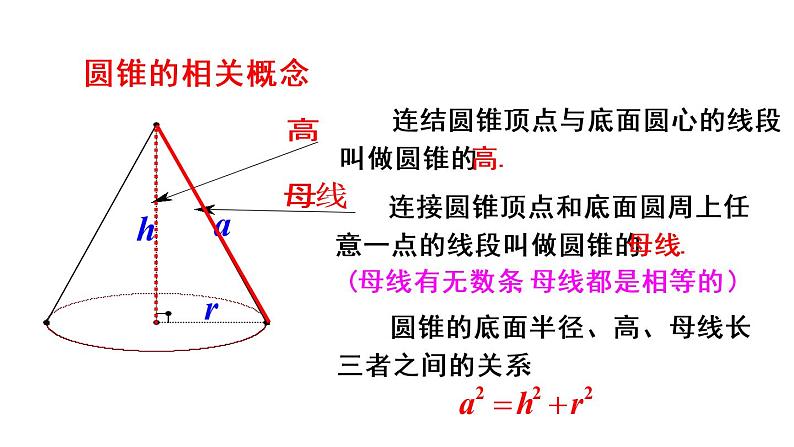
连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.
连结圆锥顶点与底面圆心的线段叫做圆锥的高.
圆锥的底面半径、高、母线长三者之间的关系:
(母线有无数条,母线都是相等的 )
圆锥的侧面展开图是什么图形？如何计算圆锥的面积？如何计算圆锥的全面积？
圆锥与侧面展开图之间的主要关系
沿着圆锥的母线，把一个圆锥的侧面展开，得到一个扇形.1.这个扇形的半径与圆锥中的哪一条线段相等？2.这个扇形的弧长与底面圆的周长有什么关系？3.圆锥的侧面积和这个扇形的面积有什么关系?
圆锥侧面展开图的扇形的半径=母线的长l
1.圆锥的母线长=扇形的半径
2.圆锥的底面周长=扇形的弧长
圆锥与侧面展开图之间的主要关系：
圆锥的侧面积=扇形的面积
一个圆锥形零件的高4cm，底面半径3cm，求这个圆锥形零件的侧面积.
答:圆锥形零件的侧面积是15πcm2.
由圆锥的两个侧面积公式推导出了n、R、r三个量之间的关系式，即nR=360r.
填空、根据下列条件求值 . (1) R=2, r=1，则n =_______.(2) R=9, r=3，则n =______ .(3) n=90°,R=4，则r =____.(4) n=60°,r= 3，则R =_____ .
蒙古包可以近似地看作由圆锥和圆柱组成的.如果想用毛毡搭建20个底面积为12 m2,高为3.2 m，外围高1.8 m的蒙古包,至少需要多少平方米的毛毡 (π取3.142，结果取整数)?
解:如图是一个蒙古包的示意图,依题意,下部圆柱的底面积12m2,高h2=1.8m;上部圆锥的高为3.2－1.8=1.4 m;
因此,搭建20个这样的蒙古包至少需要毛毡20×（22.10+14.76）≈738m2
1.圆锥的母线长为13cm，底面半径为5cm，则此圆锥的高为( )A.6cm B.8cm C.10cm D.12cm2.一个圆锥的侧面积是底面积的2倍，这个圆锥的侧面展开图扇形的圆心角是( )A.60° B.90° C.120° D.180°
3.已知圆锥的母线长为5，底面半径为3，则圆锥的表面积为( )A.15π B.24π C.30π D.39π 
4.如图，粮仓的顶部是圆锥形，这个圆锥的底面周长为32 m，母线长为7 m，为了防雨，需要在它的顶部铺上油毡，则所需油毡的面积至少为多少平方米？
解：S= ×32×7=16×7=112(m2)答：所需油毡的面积至少是112m2.
5.如图，已知圆锥的母线长AB=8cm，轴截面的顶角为60°，求圆锥全面积.解：∵AB=AC，∠BAC=60°，∴△ABC是等边三角形.∴AB=BC=AC=8cm.∴S侧=πrl=π×4×8=32π(cm2),S底=πr2=π×4×4=16π(cm2),∴S全=S侧+S底=48π(cm2).
6.Rt△ABC中，∠C=90°，AC=3，BC=4，把它分别沿三边所在直线旋转一周，求所得的三个几何体的全面积.解：AB= =5,绕AC旋转：S全1=S侧1+S底1=πr1l1+πr12=π×4×5+π×42=36π.绕BC旋转：S全2=S侧2+S底2=πr2l1+πr22=π×3×5+π×32=24π.绕AB旋转：底面半径r3= =2.4.S全3=S侧上+S侧下=πr3l2+πr3l3=π×2.4×3+π×2.4×4=16.8π.
7.如图，从一个直径是1m的圆形铁皮中剪出一个圆心角为90°的扇形，求被剪掉的部分的面积；如果将剪下来的扇形围成一个圆锥,圆锥的底面圆的半径是多少？
解：连接BC,AO,则AO⊥BC.∵OA= m,∠BAO=45°，