模拟卷06-2022年中考数学模拟热身练习卷（广东专用）

这是一份模拟卷06-2022年中考数学模拟热身练习卷（广东专用），文件包含模拟卷06-2022年中考数学模拟热身练习卷广东专用解析版docx、模拟卷06-2022年中考数学模拟热身练习卷广东专用原卷版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。
2022年广东中考数学模拟试卷06
时间：90分钟，满分：120分
一、选择题（本大题10小题，每小题3分，共30分）
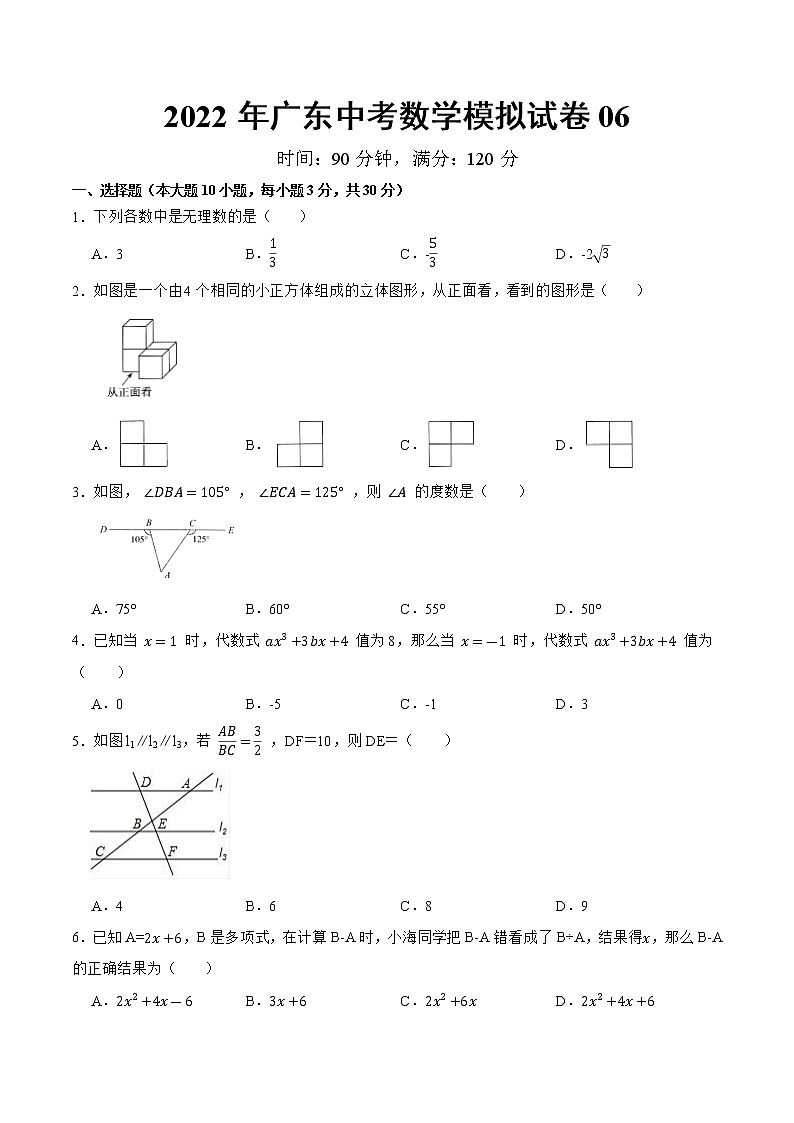
1．下列各数中是无理数的是（　　）
A．3 B．13 C．-53 D．-23
【答案】D
【解析】【解答】解：A、3是整数，是有理数，故A不符合题意；
B、13是分数，是有理数，故B不符合题意；
C、-53是分数，是有理数，故C不符合题意；
D、-23是无理数，故D符合题意.
故答案为：D.

【分析】根据有理数和无理数的定义逐项进行判断，即可得出答案.
2．如图是一个由4个相同的小正方体组成的立体图形，从正面看，看到的图形是（　　）

A． B． C． D．
【答案】A
【解析】【解答】解：从正面看有2列，从左往右每列小正方形数目分别为2，1．
故答案为：A．
【分析】根据所给的正方体对每个选项一一判断即可。
3．如图， ∠DBA=105° ， ∠ECA=125° ，则 ∠A 的度数是（　　）

A．75° B．60° C．55° D．50°
【答案】D
【解析】【解答】解： ∵∠DBA=105° ， ∠ECA=125° ，
∴∠ABC=180°-105°=75° ，
∠ACB=180°-125°=55° .
∴∠A=180°-75°-55°=50° .
故答案为：D.
【分析】根据邻补角的定义可求得 ∠ABC 和 ∠ACB ，再根据三角形内角和为180°即可求出 ∠A .
4．已知当 x=1 时，代数式 ax3+3bx+4 值为8，那么当 x=-1 时，代数式 ax3+3bx+4 值为（　　）
A．0 B．-5 C．-1 D．3
【答案】A
【解析】【解答】解：∵当 x=1 时，代数式 ax3+3bx+4 值为8，
∴a+3b+4=8，即：a+3b=4，
∴当 x=-1 时，
ax3+3bx+4 = a⋅(-1)3+3b⋅(-1)+4=-a-3b+4=-(a+3b)+4=-4+4=0.
故答案为：A.
【分析】由已知条件可得a+3b=4，当x=-1时，代数式的值为-(a+3b)+4，据此计算.
5．如图l1∥l2∥l3，若 ABBC=32 ，DF＝10，则DE＝（　　）

A．4 B．6 C．8 D．9
【答案】B
【解析】【解答】解：由题意得 ABAC=DEDF=35 ，则DE= 35×10=6 ，
故答案为：B.

【分析】根据平行线分线段成比例的性质可得ABAC=DEDF=35，再将数据代入计算即可。
6．已知A=2x+6，B是多项式，在计算B-A时，小海同学把B-A错看成了B÷A，结果得x，那么B-A的正确结果为（　　）
A．2x2+4x-6 B．3x+6 C．2x2+6x D．2x2+4x+6
【答案】A
【解析】【解答】解：由题意得：B÷A=x，
∴B=x⋅A=x(2x+6)=2x2+6x，
∴B-A=2x2+6x-2x-6=2x2+4x-6，
故答案为：A．

【分析】利用整式的加减乘除运算求解即可。
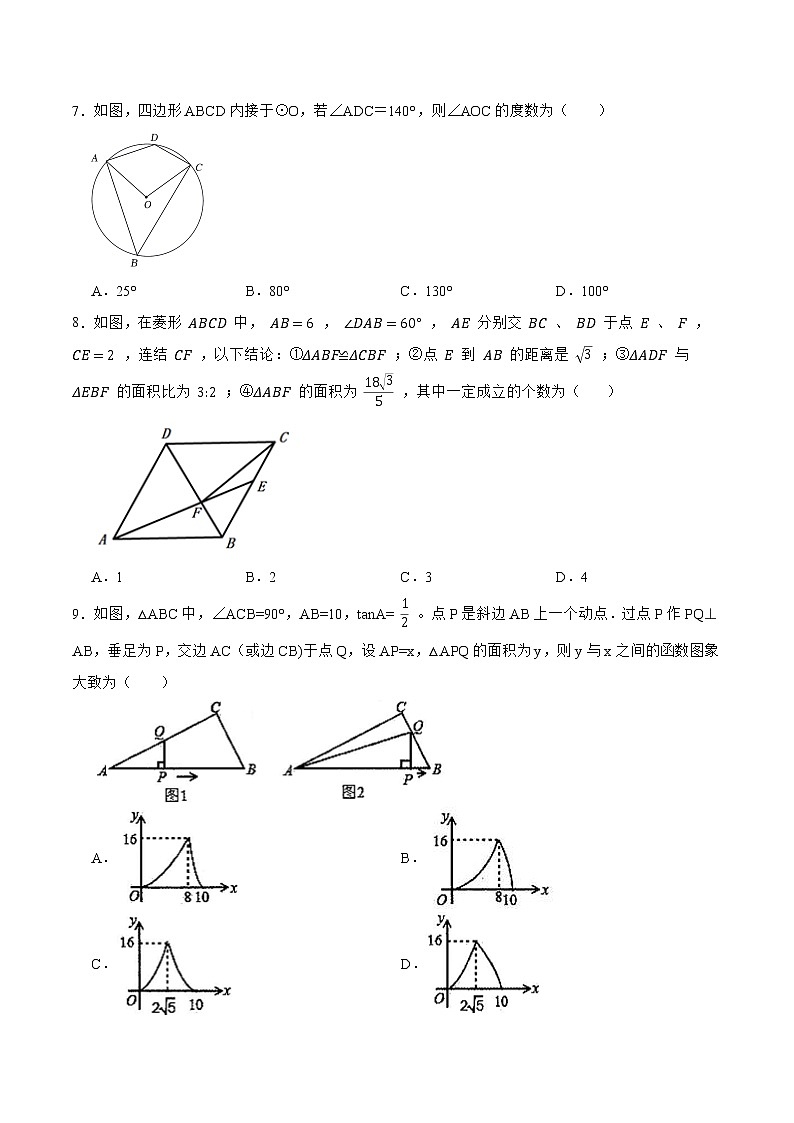
7．如图，四边形ABCD内接于⊙O，若∠ADC＝140°，则∠AOC的度数为（　　）

A．25° B．80° C．130° D．100°
【答案】B
【解析】【解答】解：∵四边形ABCD内接于⊙O，∠ADC＝140°
∴∠ABC=40°，
∴∠AOC=2∠ABC=80°，
故答案为：B

【分析】先利用圆内接四边形的性质可得∠ABC=40°，再利用圆周角的性质可得∠AOC=2∠ABC=80°。
8．如图，在菱形 ABCD 中， AB=6 ， ∠DAB=60° ， AE 分别交 BC 、 BD 于点 E 、 F ， CE=2 ，连结 CF ，以下结论：①ΔABF≌ΔCBF ；②点 E 到 AB 的距离是 3 ；③ΔADF 与 ΔEBF 的面积比为 3:2 ；④ΔABF 的面积为 1835 ，其中一定成立的个数为（　　）

A．1 B．2 C．3 D．4
【答案】B
【解析】【解答】解：①∵四边形ABCD是菱形，
∴AB=BC，∠ABC=180°-∠DAB=120°，
∴∠ABD=∠CBD=60°，
又∵BF=BF，
∴ΔABF≌ΔCBF （SAS），故①正确；
②∵BC=AB=6， CE=2 ，
∴BE=4，
过点E作EH⊥AB交AB的延长线于点H，如图1，

在Rt△EBH中，∠EBH=180°-∠ABC=60°，
∴EH=BE⋅sin60∘=23 ，
∴点E到AB的距离是 23 ，故②错误；
③∵AD∥BC，
∴△ADF∽△EBF，
∴相似比为 ADBE=64=32 ，
∴ΔADF 与 ΔEBF 的面积比为 (32)2=94 ，故③错误；
④过点F作FG⊥AB于点G，

∵AB=AD， ∠DAB=60° ，
∴△ABD是等边三角形，
∴BD=AB=6，
由③知△ADF∽△EBF，
∴DFBF=ADBE=32 ，
∴BF= 125 ，
在Rt△BFG中，∠ABD=60°，
∴FG= BF⋅sin60∘=635 ，
∴ΔABF 的面积为 12AB⋅FG=12×6×635 = 1835 ，故④正确；
故答案为：B.
【分析】由菱形的性质可得AB=BC，∠ABC=180°-∠DAB=120°，则∠ABD=∠CBD=60°，然后利用全等三角形的判定定理可判断①；易得BE=4，过点E作EH⊥AB交AB的延长线于点H，求出∠EBH的度数，然后根据三角函数的概念求出EH，据此判断②；易证△ADF∽△EBF，然后根据相似三角形的性质可判断③；过点F作FG⊥AB于点G，易得△ABD是等边三角形，则BD=AB=6，由相似三角形的性质可得BF，根据三角函数的概念求出FG，然后利用三角形的面积公式可判断④.
9．如图，△ABC中，∠ACB=90°，AB=10，tanA= 12 。点P是斜边AB上一个动点．过点P作PQ⊥AB，垂足为P，交边AC（或边CB)于点Q，设AP=x，△APQ的面积为y，则y与x之间的函数图象大致为（　　）

A． B．
C． D．
【答案】B
【解析】【解答】解：作出Rt△ABC的高CD。
在Rt△ABC中，tanA=BCAC=12 ∴ BC=12AC
设BC为k，则AC为2k,
在Rt△ABC中,AC2+BC2=AB2 即（2k）2+（k）2=102
解得 k=25
∴AC=45，BC=5
又∵12AB·CD=12AC·BC
∴CD=AC·BCAB=45×2510=4.
在Rt△ACD中,AD=AC2-CD2=80-16=8
分两种情况：
（1）如图1，当PQ与边AC相交（0≤x≤8）时，在Rt△APQ中，tanA=PQAP=12∴PQ=12AP=12x
∴y=12AP·PQ=12·x·12x=14x2

（2）如图2，当PQ与边BC相交（8＜x≤10）时，∵PQ∥CD ∴△BPQ∽△BDC ∴PQCD=BPBD即PQ4=10-x10-8 ∴PQ=-2x+20
∴y=12AP·PQ=12·x·（-2x+20）=-x2+10x
根据自变量的取值范围和y与x的函数关系式可知：选项B正确。

故答案为：B.
【分析】先利用锐角三角函数的定义、勾股定理、相似三角形的判定和性质以及等面积法用含有x的代数式表示出高PQ，然后根据三角形面积公式表示出y与x之间的函数关系式，再根据自变量的取值范围即可确定出函数的图象。注意分两种情况解决。
10．二次函数 y=ax2+bx+c(a≠0) 的部分图象如图所示，图象过点（-1，0），对称轴为直线x=2，下列结论：①4a＋b=0；②9a＋c>3b；③8a＋7b＋2c>0；④若点A（-3，y1）、点B（ -12 ，y2）、点C（ 72 ，y3）在该函数图象上，则 -43 ；⑤若方程 a(x+1)(x-5)=-3 的两根为 x1 和 x2 ，且 x1