2018年湖南省普通高中学业水平考试数学试题与答案

这是一份2018年湖南省普通高中学业水平考试数学试题与答案，共7页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。
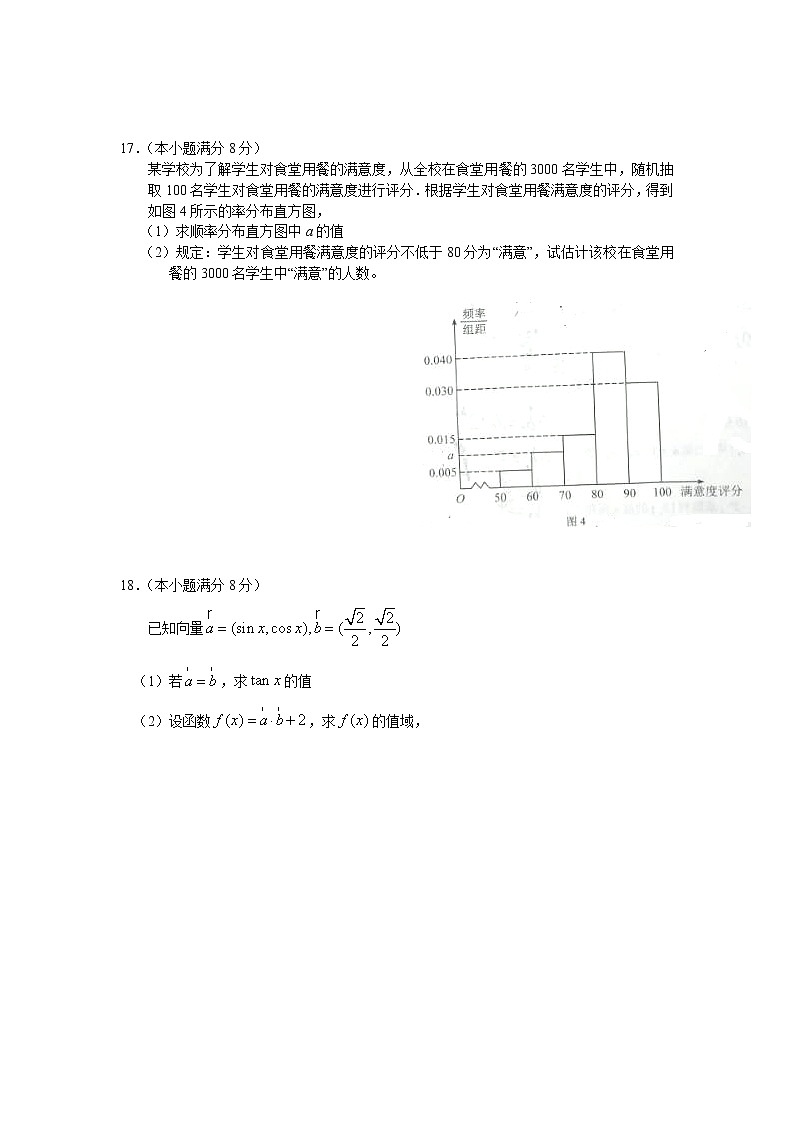
机密★启用前2018年湖南省普通高中学业水平考试数  学本试题卷包括选择题、填空题和解答题三部分，时量120分钟  满分100分一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的1．下列几何体中为圆柱的是 (       )2．执行如图1所示的程序框图，若输入x的值为10，则输出y的值为(      )A．10B．15C．25D．353．从1，2，3，4，5这五个数中任取一个数，则取到的数为偶数的概率是(     )A．                          B．C．                          D．4．如图2所示，在平行四边形ABCD中中，(     )A．                       B．C．                       D．5．已知函数y＝f（x）（）的图象如图3所示，则f（x）的单调递减区间为(      )A．                 B．C．                  D．6．已知a＞b，c＞d，则下列不等式恒成立的是 (     )A．a+c＞b＋d                B．a+d>b+cC．a-c>b-d                  D．a-b>c-d   7．为了得到函数的图象象只需将的图象向左平移 (        )A．个单位长度             B．个单位长度C．个单位长度               D．个单位长度8．函数的零点为(      )A．4          B．3        C．2            D．19．在△ABC中，已知A＝30°，B＝45°，AC＝，则BC＝(      )A．              B．        C．         D．10．过点M（2，1）作圆C：的切线，则切线条数为(      )A．0                   B．1           C．2          D．3二、填空题；本大题共5小题，每小题4分，共20分，11．直线在y轴上的截距为_____________。12．比较大小：sin25°_______sin23°（填“＞”或“＜”）13．已知集合．若，则x＝______。14．某工厂甲、乙两个车间生产了同一种产品，数量分别为60件、40件，现用分层抽样方法抽取一个容量为n的样本进行质量检测，已知从甲车间抽取了6件产品，则n＝_____。15．设x，y满足不等等式组，则z＝2x－y的最小值为________。三、解答题：本大题共5小题，共40分，解答应写出文字说明、证明过程或演步16．（本小题满分6分）已知函数（1）求的值（2）判断函数的奇偶性，并说明理由．       17．（本小题满分8分）某学校为了解学生对食堂用餐的满意度，从全校在食堂用餐的3000名学生中，随机抽取100名学生对食堂用餐的满意度进行评分．根据学生对食堂用餐满意度的评分，得到如图4所示的率分布直方图，（1）求顺率分布直方图中a的值（2）规定：学生对食堂用餐满意度的评分不低于80分为“满意”，试估计该校在食堂用餐的3000名学生中“满意”的人数。             18．（本小题满分8分）已知向量（1）若，求的值（2）设函数，求的值域，               19．（本小题满分8分）如图5所示，四棱锥P－ABCD的底面是边长为2的正方形、PA⊥底面ABCD．（1）求证：CD⊥平面PAD；（2）若E为PD的中点，三棱锥C－ADE的体积为，求四棱锥P－ABCD的侧面积             、  20．（本小题满分10分）在等差数列中，已知。（1）求（2）设，求数列的前项和（3）对于（2）中的，设，求数列中的最大项。                参考答案一、选择题题号12345678910答案BCCABADCDB二、填空题11．3      12．>    13．2    14. ．10   15．三、解答题16．解：（1）f(1)=2   （2）定义域为，所以为奇函数。17．解（1）由频率分布直方图的矩形面积和为1可知：所以     （2）样本中不低于80分的频率为由样本估计总体可得3000名学生中不低于80分的频率为约为，所以满意的人数为。故该校在校食堂用餐的3000名学生中“满意”的人数约为2100人。18．解：（1）则所以（2）因为，所以的值域为。