2022届江苏省南京外国语、金陵中学、海安中学高三5月联考考前模拟数学试题

这是一份2022届江苏省南京外国语、金陵中学、海安中学高三5月联考考前模拟数学试题，文件包含江苏省南京外国语金陵中学海安中学2022届高三下学期考前模拟数学试题5月联考解析版pdf、江苏省南京外国语金陵中学海安中学2022届高三下学期考前模拟数学试题5月联考原卷版docx等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。

数 学 2022年5月
注意事项：
1．考试结束后，将本试卷和答题卡一并交回 ．
2．本试卷中所有试题必须作答在答题卡上规定的位置，否则不给分．
3．答题前，务必将自己的姓名、准考证号等信息用黑色量水签字笔填写在答题卡的相应位置．
一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中只有一项是符合题目要求的．
1．设集合M＝{5，x2}，N＝{5x，5}．若M＝N，则实数x的值组成的集合为
A．{5} B．{1} C． {0，5} D． {0，1}
2．已知复数z＝eq \f(3＋1,1＋i)(i是虚数单位)，则eq \\ac(\S\UP7(―),z)对应的点在第 象限．
A．一 B．二 C．三 D．四
3．八音是中国古代对乐器的总称，指金、石、土、革、丝、木、匏、竹八类，每类又包括若干种乐器．现有土、丝、竹三类乐器，其中土有缶、埙2种乐器；丝有琴、瑟、筑、琵琶4种乐器；竹有箫、笛、笼3种乐器．现从这三类乐器中各选1种乐器分配给甲、乙、丙三位同学演奏，则不同的分配方案有
A．24种 B．72种 C．144种 D．288种
4．已知α∈(π，eq \f(3π,2))，若cs(α＋eq \f(π,3))＝eq \f(\r(,5),5)，则cs(α＋eq \f(π,12))＝
A．eq \f(3\r(,10),10) B．eq \f(\r(,10),10) C．－eq \f(\r(,10),10) D．－eq \f(3\r(,10),10)
5．已知eq \\ac(\S\UP7(→),OA)，eq \\ac(\S\UP7(→),OB)，eq \\ac(\S\UP7(→),OC)均为单位向量，且满足eq \f(1,2)eq \\ac(\S\UP7(→),OA)＋eq \\ac(\S\UP7(→),OB)＋eq \\ac(\S\UP7(→),OC)＝0，则eq \\ac(\S\UP7(→),AB)·eq \\ac(\S\UP7(→),AC)的值为
A．eq \f(3,8) B．eq \f(5,8) C．eq \f(7,8) D．eq \f(19,8)
6．某同学高考后参加国内3所名牌大学A，B，C的“强基计划”招生考试，已知该同学能通过这3所大学A，B，C招生考试的概率分别为x，y，eq \f(1,2)，该同学能否通过这3所大学的招生考试相互独立，且该同学恰好能通过其中2所大学招生考试的概率为eq \f(5,18)，该同学恰好通过A，B两所大学招生考试的概率最大值为
A．eq \f(25,18) B．eq \f(1,9) C．eq \f(1,6) D．eq \f(1,18)
7．正四面体P－ABC的棱长为4，若球O与正四面体的每一条棱都相切，则球O的表面积为
A．2π B．8π C．EQ \F(8\R(,2),3)π D．12π
8．若两曲线y＝x2－1与y＝alnx－1存在公切线，则正实数a的取值范围为
A．(0，2e] B．(0，e] C．[2e，＋∞) D．(e，2e]
二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．
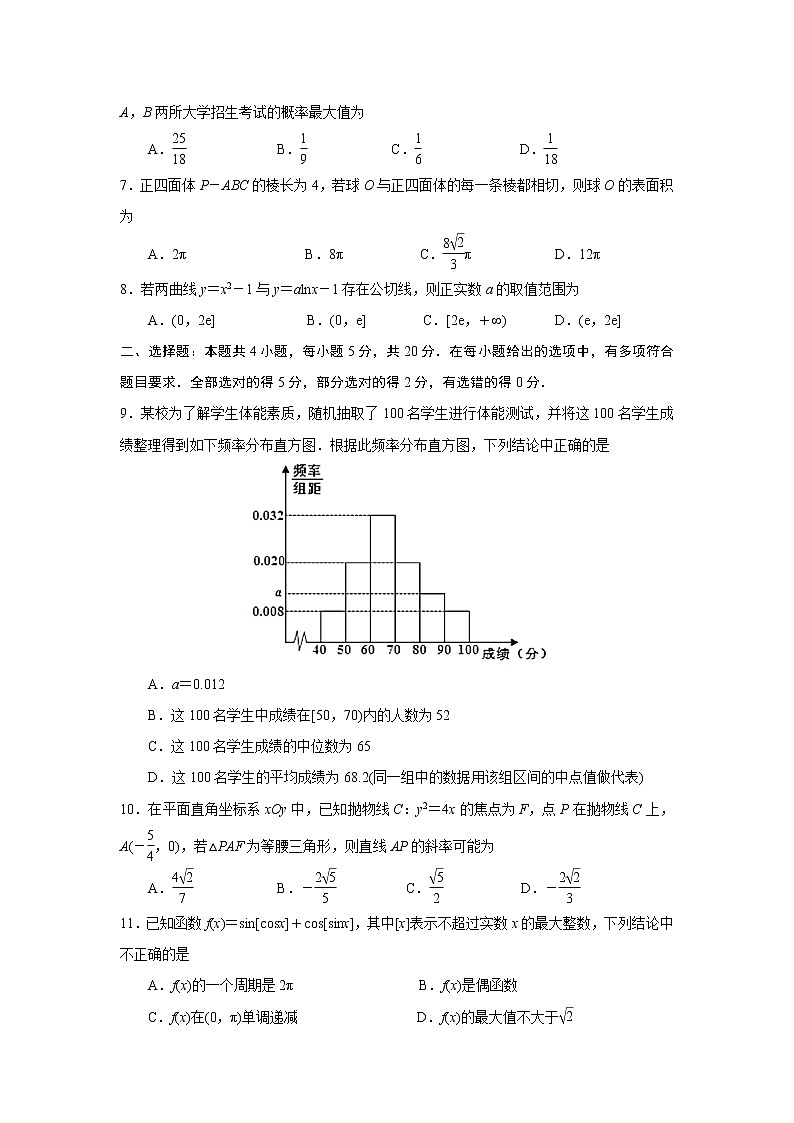
9．某校为了解学生体能素质，随机抽取了100名学生进行体能测试，并将这100名学生成绩整理得到如下频率分布直方图．根据此频率分布直方图，下列结论中正确的是
A．a＝0.012
B．这100名学生中成绩在[50，70)内的人数为52
C．这100名学生成绩的中位数为65
D．这100名学生的平均成绩为68.2(同一组中的数据用该组区间的中点值做代表)
10．在平面直角坐标系xOy中，已知抛物线C：y2＝4x的焦点为F，点P在抛物线C上，A(－eq \f(5,4)，0)，若△PAF为等腰三角形，则直线AP的斜率可能为
A．eq \f(4\r(,2),7) B．eq －\f(2\r(,5),5) C．eq \f(\r(,5),2) D．eq －\f(2\r(,2),3)
11．已知函数f(x)＝sin[csx]＋cs[sinx]，其中[x]表示不超过实数x的最大整数，下列结论中不正确的是
A．f(x)的一个周期是2π B．f(x)是偶函数
C．f(x)在(0，π)单调递减 D．f(x)的最大值不大于eq \r(,2)
12．如图，正方形ABCD－A1B1C1D1边长为1，P是A1D上的一个动点，下列结论中正确的是
A．BP的最小值为eq \f(\r(,6),2)
B．PA＋PC的最小值为eq \r(,2－\r(,2))
C．当P在直线A1D上运动时，三棱锥A－B1PC的体积不变
D．以点B为球心，eq \f(\r(,2),2)为半径的球面与面AB1C的交线长为eq \f(\r(,6),3)π
二、填空题：本题共4小题，每小题5分，共20分．
13．在eq (ax－\f(1,x))\s\up6(5)的展开式中，若含x项的系数为80，则实数a的值为________．
14．设函数y＝f(x)的图象与y＝3EQ \S\UP6(x＋m)的图象关于直线y＝x对称，若f(3)＋f(9)＝1，实数m的值为________．
15．在平面直角坐标系xOy中，已知点P(2，2)，C(5，6)．若在以点C为圆心，r半径的圆上存在不同的两点A，B，使得eq \\ac(\S\UP7(→),PA)－2\\ac(\S\UP7(→),AB)＝0，则r的取值范围为________．
16．德国数学家康托尔是集合论的创始人，以其名字命名的“康托尔尘埃”作法如下：第一次操作，将边长为1的正方形分成9个边长为eq \f(1,3)的小正方形后，保留靠角的4个，删去其余5个；第二次操作，将第一次剩余的每个小正方形继续9等分，并保留每个小正方形靠角的4个，其余正方形删去；以此方法继续下去……．经过n次操作后，共删去 个小正方形；若要使保留下来的所有小正方形面积之和不超过eq \f(1,1000)，则至少需要操作 次．(lg2＝0.3010，lg3＝0.4771)
三、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．
17．(本小题满分10分)
(1)求{an}的通项公式；
(2)若bn＝eq \f(a\s\d(n)－1,a\s\d(n)－14)，{bn}的前n项和为Tn，求Tn取得最小值时的n的值．
18．(本小题满分12分)
在△ABC中，a，b，c分别为A，B，C所对边，eq tanC＝\f(sinA＋sinB,csA＋csB)．
(1)求csC的值；
(2)若sinA＝eq \f(2\r(,7),7)，求eq \f(b,c)的值．
19．(本小题满分12分)
如图，在三棱柱ABC－A1B1C1中，底面ABC是边长为2的正三角形，侧面ACC1A1是菱形，平面ACC1A1⊥平面ABC，E，F分别是棱A1C1，BC的中点，G是棱CC1上一点，且EQ \\ac(\S\UP7(→),C\S\DO(1)G)＝tEQ \\ac(\S\UP7(→),GC)(t＞0)．
(1)证明：EF∥平面ABB1A1；
(2)若三棱锥C1－ABC的体积为1，且二面角A－EG－F的余弦值为EQ \F(4\R(,53),53)，求t的值．
20．(本小题满分12分)
自2022年3月起，新冠肺炎本土疫情已波及全国27个省份，呈现出点多、面广、频率大的特点．中国疾控中心流行病学专家表示，由于奥密克戎传染性强、隐匿性强，症状比较轻，增加了第一时间发现最早病例的难度，这就造成了多省多起疫情同时发生．某学校为了保障教学活动的正常进行，决定加强学生的核酸检测，同时为了避免过度防疫，造成人力、财力等不必要的浪费，核酸检测作如下要求：每班班级人数50人，每次按学号随机抽取30人，每周抽两次．
(1)一周内，高三(1)班的甲同学被抽取到的次数为X，求X的分布列和数学期望；
(2)设一周内，两次都被抽取到的人数为变量Y，则Y的可能取值是哪些?其中Y取到哪一个值的可能性最大?请说明理由．
21．(本小题满分12分)
在平面直角坐标系xOy中，设椭圆C：EQ \F(x\S(2),a\S(2))＋\F(y\S(2),b\S(2))＝1(a＞b＞0)的两个焦点分别为F1，F2，点P在椭圆C上，连结PF1，PF2并延长，分别交椭圆于点A，B．已知△APF2的周长为eq 8\r(,2)，△F1PF2面积最大值为4．
(1)求椭圆C的标准方程；
(2)当P不是椭圆的顶点时，试分析直线OP和直线AB的斜率之积是否为定值?若是，求出该定值，若不是，请说明理由．
22．(本小题满分12分)
已知函数f(x)＝e2x，g(x)＝m(2x＋1)，m＞0，设h(x)＝f(x)－g(x)．
(1)若函数h(x)有两个零点，求实数m的取值范围；
(2)若直线y＝g(x)是直线f(x)＝e2x的一条切线，求证：a＞b，都有eq \f(h(a)－h(b),a－b)≤2e2a－2．