




2022届北京市顺义区高三第二次统练数学试卷及参考答案
展开这是一份2022届北京市顺义区高三第二次统练数学试卷及参考答案,文件包含顺义区2022届高三第二次统练数学参考答案docx、顺义区2022届高三第二次统练数学试卷docx等2份试卷配套教学资源,其中试卷共12页, 欢迎下载使用。
顺义区2022届高三第二次统练
数学试卷
考 生 须 知 | 1.本试卷共5页,共两部分,21道小题,满分150分。考试时间120分钟。 2.在试卷和答题卡上准确填写学校名称、姓名和班级。 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。 4.在答题卡上,选择题用2B铅笔作答,其它试题用黑色字迹签字笔作答。 |
第一部分(选择题 共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
(1)函数的定义域为
(A) | (B) | (C) | (D) |
(2)如图,在复平面内,复数对应的点为,则复数
(A) | (B) | (C) | (D) |
|
|
|
|
(3)在的展开式中,常数项为
(A) | (B) | (C) | (D) |
(4)已知双曲线的一个焦点为,则双曲线的一条渐近线方程为
(A) | (B) | (C) | (D) |
(5)设等比数列的前项和为,公比为.若, 则
(A) | (B) | (C) | (D) |
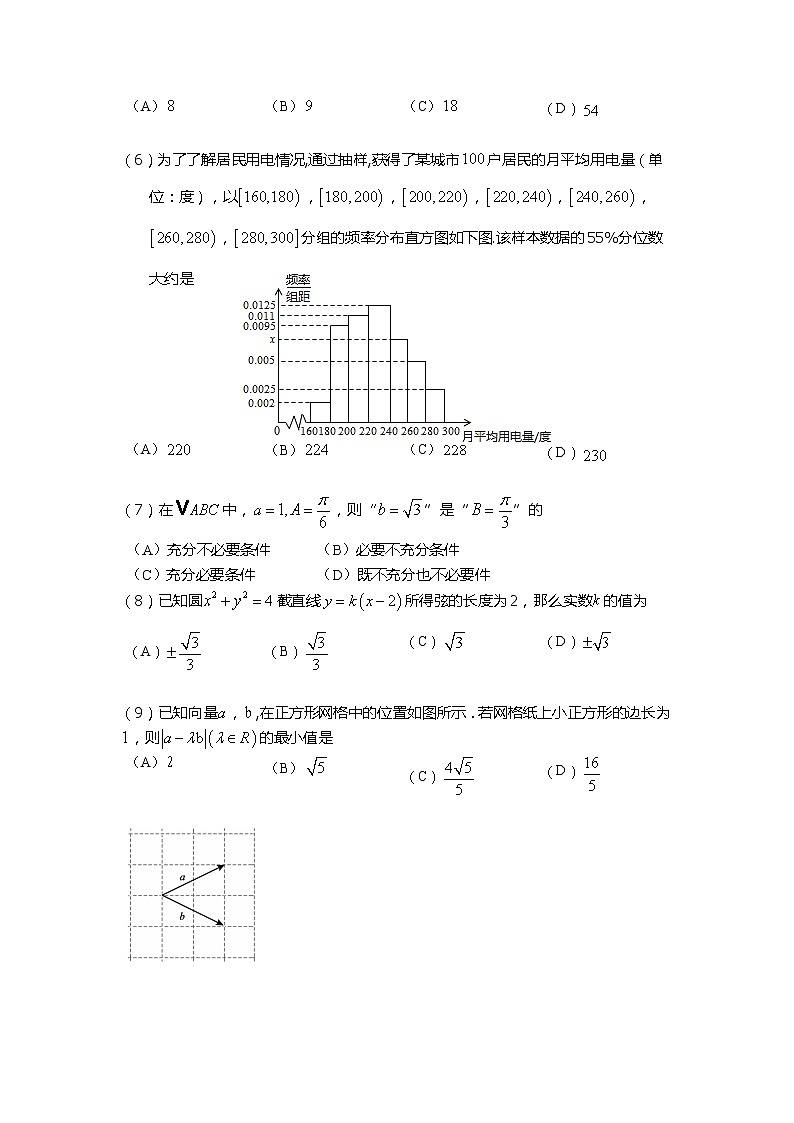
(6)为了了解居民用电情况,通过抽样,获得了某城市户居民的月平均用电量(单位:度),以,,,,,,分组的频率分布直方图如下图.该样本数据的55%分位数大约是
(A) | (B) | (C) | (D) |
(7)在中,,则“”是“”的
(A)充分不必要条件 | (B)必要不充分条件 |
|
(C)充分必要条件 | (D)既不充分也不必要件 |
|
(8)已知圆截直线所得弦的长度为2,那么实数的值为
(A) | (B) | (C) | (D) |
(9)已知向量,,在正方形网格中的位置如图所示.若网格纸上小正方形的边长为,则的最小值是
(A) | (B) | (C) | (D) |
(10)如图,设分别是长方体棱上的两个动点,点在点的左边,且满足,有下列结论:
①平面;
②三棱锥体积为定值;
③平面;
④平面平面;
其中,所有正确结论的序号是
(A)①② | (B)②③ | (C)②④ | (D)③④ |
第二部分(非选择题 共110分)
二、填空题共5道小题,每题5分。共25分,把答案填在答题卡上。
(11)已知集合,,则 ____________.
(12)已知函数,若,则_____________.
(13)已知抛物线的焦点为,点在抛物线上,垂直抛物线准线于点.若为等边三角形,则点的横坐标为___________,的面积是________________.
(14)已知是定义在上的函数,其值域为,则可以是________.(写出一个满足条件的函数表达式即可)
(15)向量集合,对于任意,,以及任意,都有,则称集合是“凸集”,现有四个命题:
①集合是“凸集”;
② 若为“凸集”,则集合也是“凸集”;
③若都是“凸集”,则也是“凸集”;
④若都是“凸集”,且交集非空,则也是“凸集”.
其中,所有正确的命题的序号是_____________________.
三、解答题共6道题,共85分。解答应写出文字说明,证明过程或演算步骤。
(16)(本小题14分)已知函数.
(I)求在区间上的最大值和最小值;
(II)设,求的最小正周期.
(17)(本小题14分)如图,在正方体中,为的中点.
(I)过点作出一条与平面平行的直线,并说明理由;
(II)求直线与平面所成角的正弦值.
(18)(本小题14分)为了解顺义区某中学高一年级学生身体素质情况,对高一年级的进行了抽测,采取如下方式抽样:每班随机各抽10名学生进行身体素质监测.经统计,每班10名学生中身体素质监测成绩达到优秀的人数散点图如下(轴表示对应的班号,轴表示对应的优秀人数):
(I)若用散点图预测高一年级学生身体素质情况,从高一年级学生中任意抽测1人,求该生身体素质监测成绩达到优秀的概率;
(II)若从以上统计的高一(4)班的10名学生中抽出2人,设表示2人中身体素质监测成绩达到优秀的人数,求的分布列及其数学期望;
(III)假设每个班学生身体素质优秀的概率与该班随机抽到的10名学生的身体素质优秀率相等.现在从每班中分别随机抽取1名同学,用“”表示第班抽到的这名同学身体素质优秀,“”表示第班抽到的这名同学身体素质不是优秀().写出方差的大小关系(不必写出证明过程).
(19)(本小题14分)已知椭圆过定点,离心率.
(I)求椭圆的标准方程;
(II)斜率为的直线与椭圆交于两点,为坐标原点,求面积的最大值及此时直线的方程.
(20)(本小题15分)若函数.
(I)判断方程解的个数,并说明理由;
(II)当,设,求的单调区间;
(21)(本小题14分)设正整数数列满足.
(I)若,请写出所有可能的取值;
(II)记集合,证明:若集合存在一个元素是3的倍数,则的所有元素都是3的倍数;
(III)若为周期数列,求所有可能的取值.
相关试卷
这是一份顺义区2022届高三第二次统练数学试卷,共13页。试卷主要包含了填空题共5道小题,每题5分,解答题共6道题,共85分等内容,欢迎下载使用。
这是一份2021北京顺义区高三下学期第二次统练数学试题缺答案,共5页。
这是一份2021北京顺义区高三下学期第二次统练数学试题含答案,共15页。












