高考数学圆锥曲线一轮复习——解析几何20讲

这是一份高考数学圆锥曲线一轮复习——解析几何20讲，文件包含1直线与方程doc、8中点弦问题--椭圆垂径定理doc、6椭圆的简单几何性质doc、16抛物线的焦点弦doc、3直线与圆的位置关系doc、10双曲线的标准方程doc、13双曲线的离心率计算doc、5椭圆的标准方程doc、18极点极线结构及非对称韦达定理doc、7直线与椭圆的位置关系及弦长计算doc、9椭圆离心率的计算doc、15抛物线的几何性质doc、14抛物线的标准方程doc、11双曲线的几何性质doc、2圆的标准方程与一般方程doc、20解析几何中的几何方法doc、17阿基米德三角形doc、4圆与圆的位置关系doc、12直线与双曲线的位置关系doc、19与斜率和斜率积有关的定点定值doc等20份课件配套教学资源，其中PPT共0页， 欢迎下载使用。
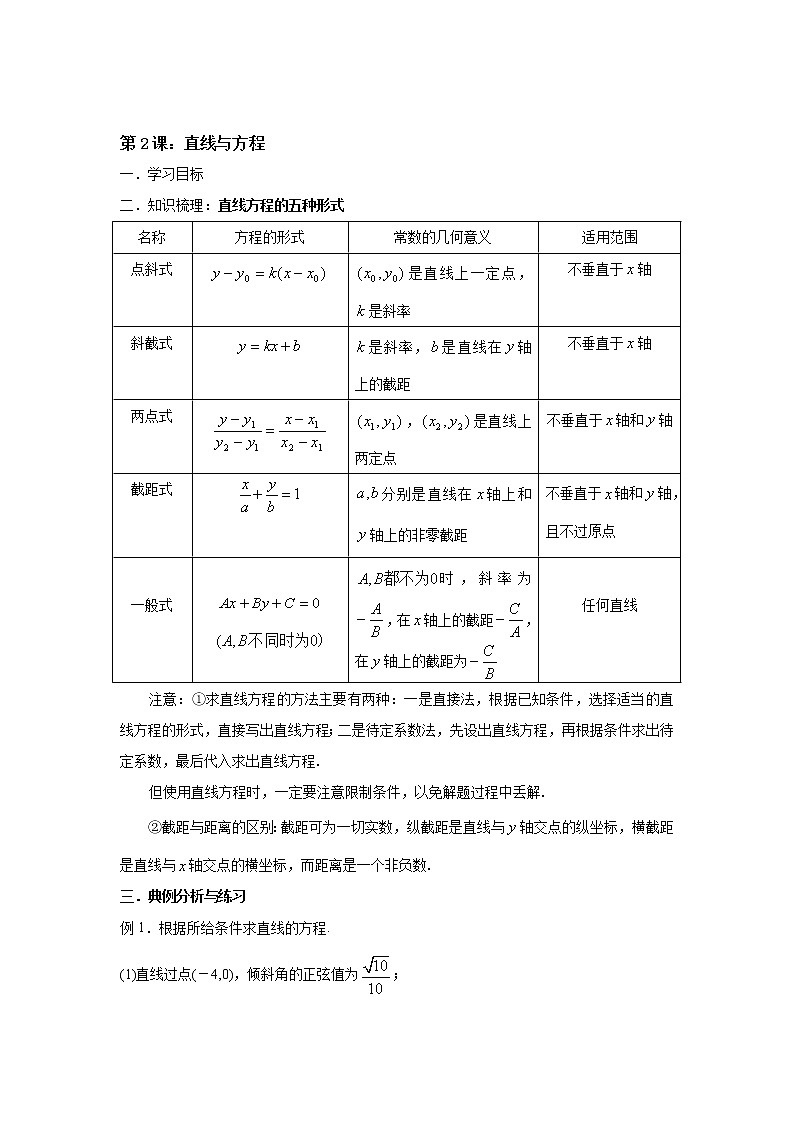
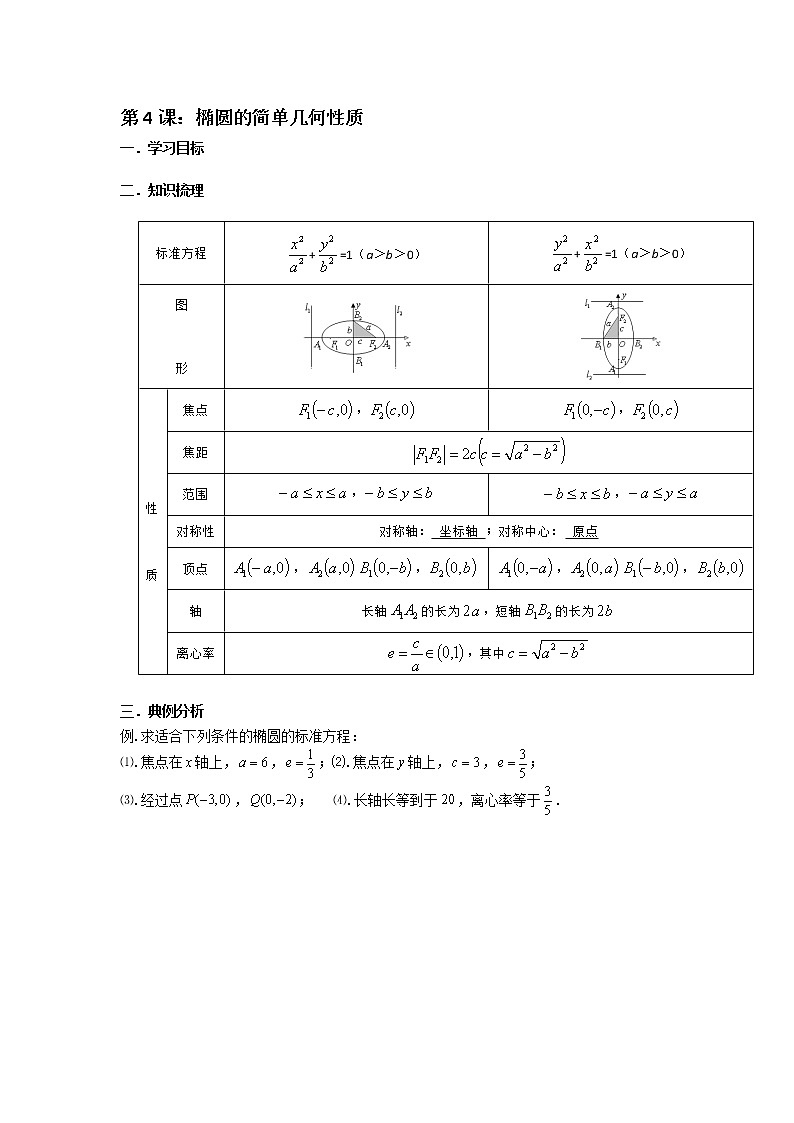
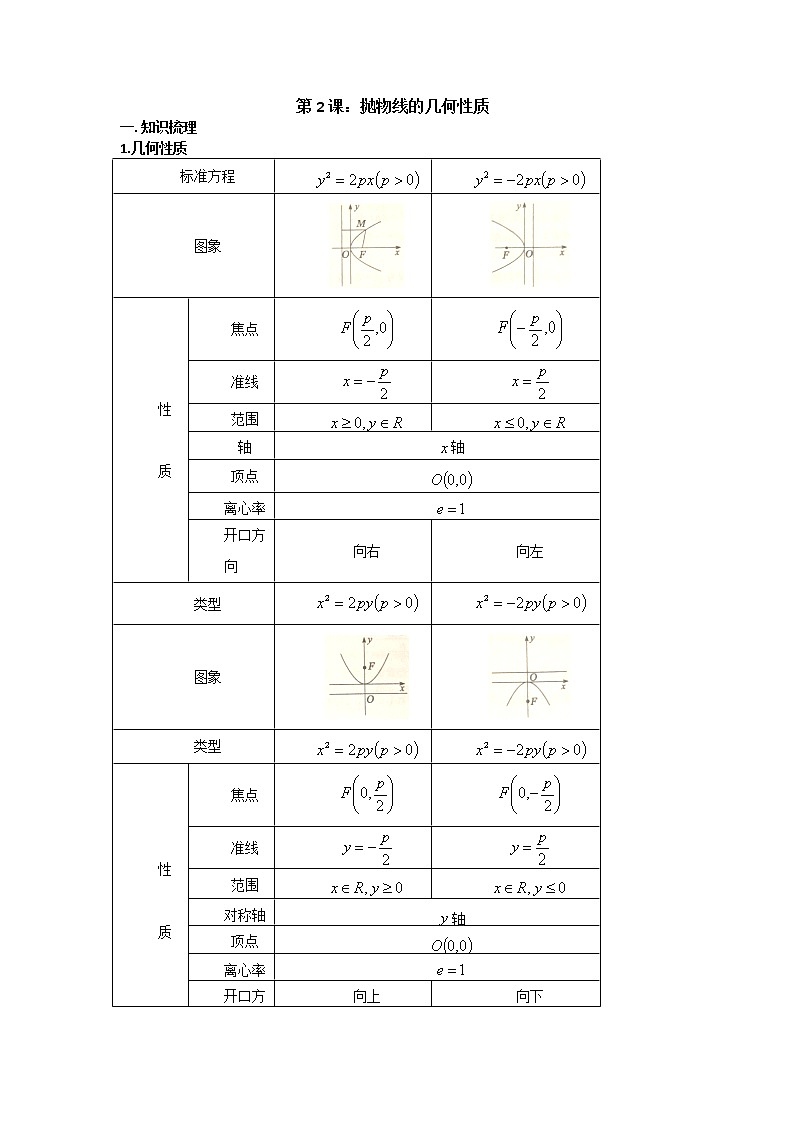
课题1：直线与方程第1课：倾斜角与斜率一．学习目标二．知识梳理： （1）直线的倾斜角定义：当直线与轴相交时，我们取轴作为基准，轴正向与直线向上方向之间所成的角叫做直线的倾斜角.当直线与轴平行或重合时，规定它的倾斜角为.倾斜角的范围为.（2）直线的斜率：定义：一条直线的倾斜角的正切值叫做这条直线的斜率，斜率常用小写字母表示，即.倾斜角是的直线，斜率不存在.（3） 过两点的直线的斜率公式：经过两点的直线的斜率公式：当时，；当时，斜率不存在.注：①任何直线都有倾斜角，但不是任何直线都有斜率，倾斜角是的直线的斜率不存在.②斜率随倾斜角的变化规律：倾斜角斜率，增大，增大不存在，增大，增大③可以用斜率来证明三点共线，即若，则三点共线. 三．典例分析与练习题1．在直角坐标系中，直线的倾斜角是（  ）A．30° B．60° C．120° D．150°2．若直线过点，则此直线的倾斜角是 （   ）A．30° B．45° C．60° D．90°3．直线的倾斜角是（）．A． B． C． D．4．若三点在同一直线上，则实数等于（   ）A． B．11 C． D．35．直线，的倾斜角是（    ）A． B． C． D．                     第2课：直线与方程一．学习目标二．知识梳理：直线方程的五种形式名称方程的形式常数的几何意义适用范围点斜式是直线上一定点，是斜率不垂直于轴斜截式是斜率，是直线在轴上的截距不垂直于轴两点式，是直线上两定点不垂直于轴和轴截距式分别是直线在轴上和轴上的非零截距不垂直于轴和轴，且不过原点 一般式 时，斜率为，在轴上的截距，在轴上的截距为 任何直线注意：①求直线方程的方法主要有两种：一是直接法，根据已知条件，选择适当的直线方程的形式，直接写出直线方程；二是待定系数法，先设出直线方程，再根据条件求出待定系数，最后代入求出直线方程.但使用直线方程时，一定要注意限制条件，以免解题过程中丢解.②截距与距离的区别：截距可为一切实数，纵截距是直线与轴交点的纵坐标，横截距是直线与轴交点的横坐标，而距离是一个非负数.三．典例分析与练习例1．根据所给条件求直线的方程.(1)直线过点(－4,0)，倾斜角的正弦值为；(2)直线过点(－3,4)，且在两坐标轴上的截距之和为12；(3)直线过点(5,10)，且到原点的距离为5.例2．中，顶点，AC边所在直线方程为，AB边上的高所在直线方程为．（1）求AB边所在直线的方程；（2）求AC边的中线所在直线的方程．   四．练习题1．经过点且在两坐标轴上截距相等的直线是（    ）A． B． C．或 D．或2．已知直线过点，且倾斜角为直线：的倾斜角的2倍，则直线的方程为（   ）A． B．C． D．3．过点且与直线：平行的直线的方程是（   ）A． B．C． D．4．已知中有，，且，则边上的中线所在直线方程为　　A． B． C． D．5．已知直线在两坐标轴上的截距相等，则实数　　A．1 B． C．或1 D．2或16．无论 取何实数，直线恒过一定点，则该定点坐标为（  ）A．  B． C． D．7．过点且在两坐标轴上截距相等的直线有（   ）A．1条    B．2条    C．3条    D．4条8．过点且与点距离最大的直线方程是（）A． B．C． D．9．点到直线（R）的距离的最大值为A． B． C．2 D．10．已知直线：.（1）若直线不经过第四象限，求的取值范围；（2）若直线交轴负半轴于点，交轴正半轴于点，为坐标原点，设的面积为4，求直线的方程.                第3课：直线与直线位置关系一．学习目标二．知识梳理1．两条直线的交点若直线：和：相交，则交点坐标是方程组的解.2．两条直线位置关系的判定（1）利用斜率判定若直线和分别有斜截式方程：和：，则①直线∥的等价条件为.②直线与重合的等价条件为.③直线与相交的等价条件为；特别地，的等价条件为.若与斜率都不存在，则与平行或重合.若与中的一条斜率不存在而另一条斜率为，则与垂直.（2）用直线一般式方程的系数判定设直线：，：，则①直线∥的等价条件为.②直线与重合的等价条件为.③直线与相交的等价条件为；特别地， 的等价条件为.注：与平行的直线方程一般可设为的形式，与垂直的直线方程一般可设为的形式.（3）用两直线联立的方程组的解的个数判定设直线：，：，将这两条直线的方程联立，得方程组，若方程组有惟一解，则与相交，此解就是，交点的坐标；若方程组无解，此时与无公共点，则∥；若方程组有无数个解，则与重合.3. 直线系问题（1）设直线：和：若与相交，则表示过与的交点的直线系（不包括）；若∥，则上述形式的方程表示与与平行的直线系.（2）过定点的旋转直线系方程为（不包括）；斜率为的平行直线系方程为.    注：直线系是具有某一共同性质的直线的全体，巧妙地使用直线系，可以减少运算量，简化运算过程.三．典例分析与练习1．若直线与平行,则的值为（    ）A．-1 B．1 C．-1或2 D．±12．设，则“”是“直线与直线平行”的（    ）A．充分不必要条件 B．必要不充分条件C．充分必要条件 D．既不充分也不必要条件3．已知直线：，：，若，则（    ）A． B．1 C．-1 D．不存在4．已知直线：与：平行，则的值是（   ）.A．或 B．或 C．或 D．或5．已知直线：，：，：，若且，则的值为　　A． B．10 C． D．2 6．已知直线，直线．（1）若，求实数的值；（2）若，求实数的值．     7．已知直线，与直线．（1）若，求的值；（2）若，求的值.     8．已知的顶点边上的中线所在直线方程为，边上的高所在直线方程为.求（1）顶点的坐标；（2）直线的方程.       9．已知中，，，，，垂足为．（1）求直线的方程；（2）求过点且平行于边的直线方程．     10．已知直线：，．（1）证明：直线恒过定点；（2）设是坐标原点，，若，求的值．                                          第4课：距离公式与对称问题1.距离公式（1）两点间的距离公式平面上的两点间的距离.特别地，原点与任一点的距离.若轴时，；若轴时，.（2）点到直线的距离公式已知点，直线：，则点到直线的距离.已知点，直线：，则点到直线的距离.已知点，直线：，则点到直线的距离.注：用此公式求解点到直线距离问题时，直线方程要化成一般式.（3）两条平行直线间的距离公式已知两平行直线：和：，若点在上，则两平行直线和的距离可转化为到直线的距离.已知两平行直线：和：，则两直线和的距离.注：用此公式求解两平行直线间的距离时，直线方程要化成一般式，并且项的系数必须对应相等.2.对称问题（1）中心对称①点关于点的对称点关于的对称点为.②直线关于点的对称在已知直线上取两点，利用中点坐标公式求出它们关于已知点对称的两点的坐标，再由两点式求出直线的方程，或者求出一个对称点，再利用∥，由点斜式求出直线的方程，或者在所求直线上任取一点，求出它关于已知点的对称点的坐标，代入已知直线，即可得到所求直线的方程.(2）轴对称①点关于直线的对称点关于的对称点为,则有,由此可求出.特别地, 点关于的对称点为，点关于的对称点为.②直线关于直线的对称此类问题一般转化为点关于直线的对称问题来解决，有两种情况：一是已知直线与对称直线相交，一是已知直线与对称直线平行.三．典例分析与练习题1．点关于直线对称的点的坐标是（    ）A． B． C． D．2．设直线 与直线的交点为,则到直线的距离最大值为(    )A． B． C． D．3．已知直线(3k－1)x＋(k＋2)y－k＝0，则当k变化时，所有直线都通过定点(   )A．(0,0) B．(，) C．(，) D．(，)4．已知直线过定点，点在直线上，则的最小值是（    ）A． B． C． D．5．平行线与之间的距离等于（    ）．A． B． C． D．6．若点到直线的距离为1，则的值为（    ）A． B． C．或 D．或7．已知方程（2＋λ）x－（1＋λ）y－2（3＋2λ）＝0与点P（－2，2）.（1）证明：对任意的实数λ，该方程都表示直线，且这些直线都经过同一定点，并求出这一定点的坐标；（2）证明：该方程表示的直线与点P的距离d小于.    8．已知直线l：x＋2y－2＝0.（1）求直线l1：y＝x－2关于直线l对称的直线l2的方程；（2）求直线l关于点A(1,1)对称的直线方程．    9．已知直线l：3x－y＋3＝0，求：(1)点P(4,5)关于l的对称点；(2)直线x－y－2＝0关于直线l对称的直线方程；(3)直线l关于(1,2)的对称直线．    本章知识结构