2021-2022学年江西省赣州市瑞金市八年级（下）期中数学试卷（含解析）

2021-2022学年江西省赣州市瑞金市八年级（下）期中数学试卷

一．选择题（本题共6小题，共18分）

1. 与是同类二次根式的是

A.  B.  C.  D.

2. 下列运算中，正确的是

A.  B.  C.  D.

3. 已知的三个内角分别为、、，三边分别为、、，下列条件不能判定是直角三角形的是

A. ：：：： B.
C.  D. ：：：：

4. 如图，▱中，平分，，则

A.
B.
C.
D.

5. 如图，在平行四边形中，于，于，若，，平行四边形的周长为则平行四边形的面积为

A.
B.
C.
D.

6. 如图，长方体的长为，宽为，高为，点离点的距离为，一只蚂蚁如果要沿着长方体的表面从点爬到点，需要爬行的最短路程是

A.
B.
C.
D.

二．填空题（本题共6小题，共18分）

7. 如果代数式有意义，则的取值范围是______．
8. 如图所有四边形都是正方形，所有三角形都是直角三角形，其中最大的正方形边长为，则正方形、、、的面积和为______．
   
    

9. 如图，在平行四边形中，、分别是、上的点，请添加一个条件，使得四边形为平行四边形，则添加的条件是______ 答案不唯一，添加一个即可．

10. 比较大小：______填“”，“”，“”号
11. 如图，在中，，，，、分别是和边上的点，把沿着直线折叠，若点落在边上，则的取值范围是______．
     

12. 在平行四边形中，平分，交于点，平分，交于点，，，则的长为______．

三．计算题（本题共1小题，共8分）

13. 计算：；
    ．

四．解答题（本题共10小题，共76分）

14. 在中，，，求的长．
    在中，，，，判断是否是直角三角形．
15. 已知，，求下列各式的值．
    ；
    ．
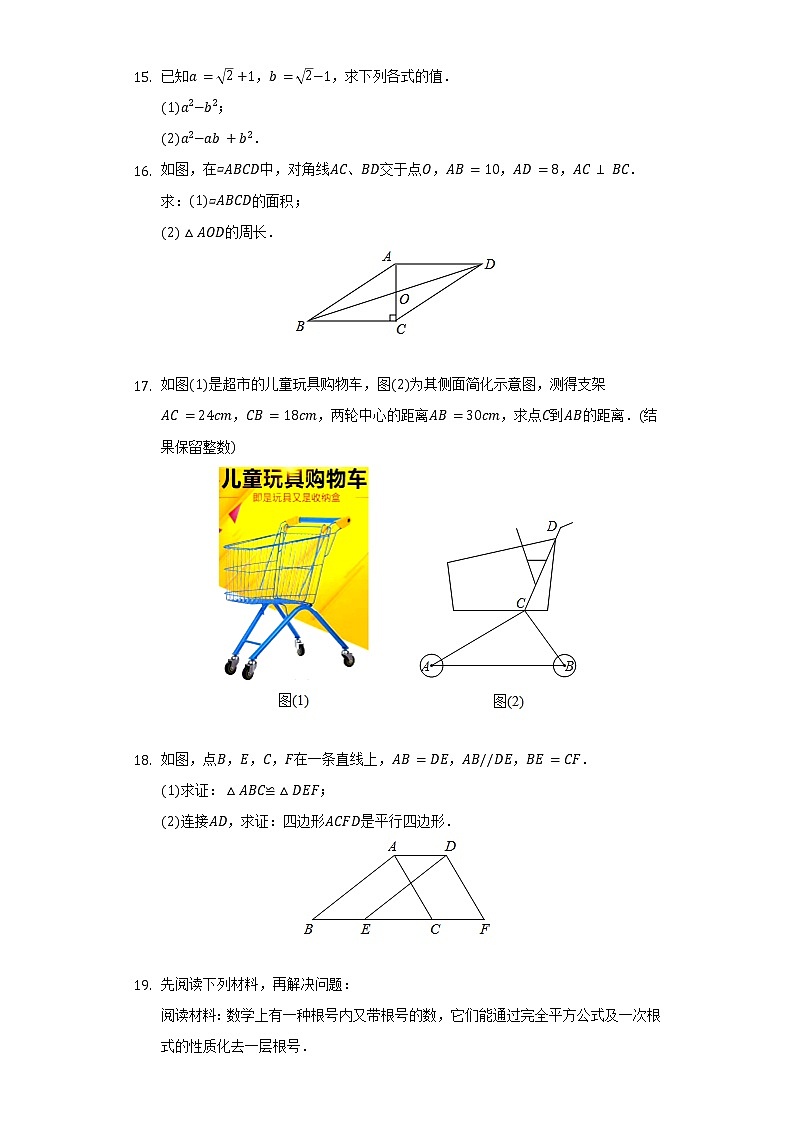
16. 如图，在▱中，对角线、交于点，，，．
    求：▱的面积；
    的周长．

17. 如图是超市的儿童玩具购物车，图为其侧面简化示意图，测得支架，，两轮中心的距离，求点到的距离．结果保留整数

18. 如图，点，，，在一条直线上，，，．
    求证：≌；
    连接，求证：四边形是平行四边形．

19. 先阅读下列材料，再解决问题：
    阅读材料：数学上有一种根号内又带根号的数，它们能通过完全平方公式及一次根式的性质化去一层根号．
    例如：．
    解决问题：
    化简下列各式：
    ；
    ．
20. 如图，在边长为的小正方形组成的网格中，的三个顶点均在格点上，请按要求完成下列各题．
    画出关于直线对称的；
    的面积为______；
    试判断的形状并说明理由．
    
     

21. 如图，平分，，若，则______．
    探究：如图，四边形，平分，，求证：．
    应用：如图，四边形，平分，，，，．
    求的长．

22. 在初、高中阶段，要求二次根式化简的最终结果中分母不含有根号，也就是说当分母中有无理数时，要将其化为有理数，实现分母有理化，比如：
    ；
    
    试试看，将下列各式进行化简：
    ；
    ；
    ．
23. 如图，已知在中，，，，是上的一点，，点从点出发沿射线方向以每秒个单位的速度向右运动．设点的运动时间为，连接．
    当秒时，求的长度；
    当为等腰三角形时，求的值；
    过点作于点，连接，在点的运动过程中，当平分时，直接写出的值．

答案和解析

1.【答案】

【解析】解：选项，，故该选项不符合题意；
选项，是最简二次根式，被开方数不是，故该选项不符合题意；
选项，，故该选项不符合题意；
选项，，故该选项符合题意；
故选：．
将各选项化简，被开方数是的二次根式是的同类二次根式，从而得出答案．
本题考查了同类二次根式，二次根式的性质与化简，掌握一般地，把几个二次根式化为最简二次根式后，如果它们的被开方数相同，就把这几个二次根式叫做同类二次根式是解题的关键．
 

2.【答案】

【解析】解：、，故此选项错误；
B、，故此选项错误；
C、，故此选项错误；
D、，正确．
故选：．
直接利用二次根式的性质分别化简得出答案．
此题主要考查了二次根式的性质与化简，正确掌握二次根式的性质是解题关键．
 

3.【答案】

【解析】解：、：：：：，，故不能判定是直角三角形；
B、，，，故能判定是直角三角形；
C、，，故能判定是直角三角形；
D、，故能判定是直角三角形；
故选：．
由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方或最大角是否是即可．
本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，可利用勾股定理的逆定理和直角三角形的定义判断．
 

4.【答案】

【解析】解：在▱中，
，
，
平分，
，
又，
．
故选：．
根据平行四边形的性质和角平分线的性质求解．
本题利用了两直线平行，同旁内角互补，内错角相等和角的平分线的性质．
 

5.【答案】

【解析】解：设，则，根据“等面积法”得
，解得，
平行四边形的面积故选D．
已知平行四边形的高、，设，则，根据“等面积法”列方程，求，从而求出平行四边形的面积．
本题应用的知识点为：平行四边形一组邻边之和为平行四边形周长的一半，平行四边形的面积底高，可用两种方法表示．
 

6.【答案】

【解析】解：只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形，如图：
长方体的宽为，高为，点离点的距离是，
；
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形，如图：
长方体的宽为，高为，点离点的距离是，
；
只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形，如图：
长方体的宽为，高为，点离点的距离是，
；
，
蚂蚁爬行的最短距离是．
故选：．
要求长方体中两点之间的最短路径，最直接的作法，就是将长方体侧面展开，然后利用两点之间线段最短解答．
本题考查的是平面展开最短路径问题，根据题意画出长方体的侧面展开图，根据勾股定理求解是解答此题的关键．
 

7.【答案】

【解析】解：由题意可得：，
解得：，
故答案为：．
根据二次根式有意义的条件列不等式求解．
本题考查二次根式有意义的条件，掌握二次根式有意义的条件被开方数为非负数是解题关键．
 

8.【答案】

【解析】解：

根据勾股定理可得面积面积面积，面积面积面积，面积面积面积，
、、、的面积和平方厘米
故答案为：．
根据勾股定理的几何意义解答．
此题考查勾股定理问题，灵活应用勾股定理以及正方形的性质来解决问题是关键．
 

9.【答案】

【解析】解：四边形平行四边形，
，，
，
，
，
四边形为平行四边形．
故答案为：．
根据平行四边形的性质可得，，添加，即可得，进而可得结论．
本题考查了平行四边形的判定与性质，解决本题的关键是掌握平行四边形的判定与性质．
 

10.【答案】

【解析】解：，，
，
，
故答案为：．
先把根号外的因式移入根号内，再比较即可．
本题考查了实数的大小比较法则和二次根式的性质，能选择适当的方法比较大小是解此题的关键．
 

11.【答案】

【解析】解：当点折叠后落在点上时，此时最长为，
当点折叠后落在点上时，此时最短，连接，如图，

此时垂直平分，，设，则，
在中，，
，
解得，
故答案为．
需要分情况讨论点落在点或者点处时的长．
本题主要考查了翻折变换的性质和勾股定理，解题关键是能够推断出的最大值和最小的位置．
 

12.【答案】或

【解析】解：四边形为平行四边形，，
，，
，
平分，
，
，
，
同理，
如图，，
，
，
如图，，
，
，
综上所述，的长为或，
故答案为：或．
根据平行四边形的性质可得，结合角平分线的定义，等腰三角形的性质可求解，，由即可求得的长．
本题主要考查平行四边形的性质，角平分线的定义，等腰三角形的性质，证明，是解题的关键．
 

13.【答案】解：

．
．

．

【解析】先利用二次根式的性质化简，再利用二次根式的加减混合运算法则计算．
直接利用二次根式的乘法和除法运算法则计算．
本题考查二次根式的乘除运算、二次根式的加减运算，正确掌握相关运算法则是解题的关键．
 

14.【答案】解：由勾股定理得：；

，，，
，，
，
是直角三角形．

【解析】根据勾股定理得出，再代入求出答案即可；
先分别求出两小边的平方和和最长边的平方，再看看是否相等即可．
本题考查了勾股定理和勾股定理的逆定理，能灵活运用定理进行计算是解此题的关键，注意：如果一个三角形的两边、的平方和等于第三边的平方，那么这个三角形是直角三角形．
 

15.【答案】解：，
，，
原式

；
当，时，



．

【解析】直接利用平方差公式分解因式，进而代入计算即可得出答案；
直接代入，然后根据乘法公式计算即可得出答案．
本题主要考查了二次根式的加减法和乘法，熟练掌握乘法公式是解决问题的关键．
 

16.【答案】解：四边形是平行四边形，，
，
，
，
在中，由勾股定理得，

；
四边形是平行四边形，，
，，
，，
，
，
．

【解析】根据平行四边形的性质和勾股定理以及平行四边形的面积公式即可得到结论；
根据平行四边形的性质和勾股定理以及三角形的周长公式即可得到结论．
此题主要考查了平行四边形的性质以及勾股定理，正确得出的长是解题关键．
 

17.【答案】解：过点作于点，则的长即点到的距离，
在中，，，，
，，
，
为直角三角形，即，
，
，即，
，
答：点到的距离约为．

【解析】过点作于点，则的长即点到的距离，根据勾股定理的逆定理得到为直角三角形，即，根据三角形的面积公式即可得到结论．
本题考查了勾股定理的应用，三角形的面积公式，勾股定理的逆定理，正确的识别图形是解题的关键．
 

18.【答案】证明：，
，
，
，
即，
在和中，
，
≌；
由得：≌，
，，
，
四边形是平行四边形．

【解析】由证明≌即可；
由全等三角形的性质得，，则，即可得出结论．
本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的性质等知识，熟练掌握平行四边形的判定，证明≌是解题的关键．
 

19.【答案】解：


；



．

【解析】首先把被开方数拆项，再化为完全平方的形式，最后根据二次根式的性质化简；
首先把被开方数拆项，再化为完全平方的形式，最后根据二次根式的性质化简．
本题考查二次根式的性质与化简、完全平方公式，熟练掌握二次根式的性质，把被开方数拆项，化为完全平方的形式是解题关键．
 

20.【答案】

【解析】解：如图所示；

的面积


．
故答案为：；

由勾股定理得，，
，
，
，
，
，
是直角三角形．
根据网格结构找出点、、关于直线的对称点、、的位置，然后顺次连接即可；
根据三角形的面积等于三角形所在的矩形面积减去四周三个直角三角形的面积列式计算即可得解；
利用勾股定理列式求出、、，再根据勾股定理逆定理解答．
本题考查了利用轴对称变换作图，勾股定理，勾股定理逆定理，三角形的面积，熟练掌握网格结构并准确找出对应点的位置是解题的关键．
 

21.【答案】

【解析】解：平分，
，
在和中，
，
≌，
，
故答案为：；
证明：在上截取，连接，如图所示：

平分，
，
在和中，
，
≌，
，，
，
，
，
，
，
；
解：如图，在上截取，连接，过作于，

由同理可得，，
，
，
是等腰直角三角形，
，
，
，，
，
在中，由勾股定理得：．
证≌，再由全等三角形的性质即可得出答案；
在上截取，连接，证≌，得，，再证，得，即可得出结论；
连接，在上截取，连接，过作于，同得，，再证是等腰直角三角形，得，，则，然后由勾股定理即可得出答案．
本题是四边形综合题目，考查了全等三角形的判定与性质，角平分线定义，等腰直角三角形的判定与性质，勾股定理等知识，本题综合性强，解题的关键是学会添加辅助线，构造出全等三角形，属于中考常考题型．
 

22.【答案】解：；
；
原式


．

【解析】仿照材料方法即可化简；
仿照材料方法即可化简；
先将各数分母有理化，再合并即可．
本题考查二次根式的分母有理化，解题的关键式读懂题意，能将二次根式分母有理化．
 

23.【答案】解：根据题意，得，
，
在中，，
根据勾股定理，得．
答：的长为．

在中，，，
根据勾股定理，得，
为等腰三角形，
若，则，
在中，根据勾股定理得，，解得．
若，则，解得；
若，则，，解得；
即满足条件的的值为或或．

点在线段上时，过点作于，如图所示：
则，
，
平分，
，
又，
≌，
，，
，
，
，
在中，由勾股定理得：，
解得：；
点在线段的延长线上时，过点作于，如图所示：
同得：≌，
，，
，
，
，
在中，由勾股定理得：，
解得：；
综上所述，在点的运动过程中，当的值为或时，平分．

【解析】根据动点的运动速度和时间先求出，再根据勾股定理即可求解；
根动点运动过程中形成三种等腰三角形，分情况即可求解；
分两种情况：点在线段上时，过点作于，先证≌，得出，，再由勾股定理求出，则，然后在中，由勾股定理得出方程，解方程即可；
点在线段的延长线上时，过点作于，同得≌，得出，，再由勾股定理得，则，然后在中，由勾股定理得出方程，解方程即可．
本题是三角形综合题，考查了全等三角形的判定与性质、勾股定理、等腰三角形的性质以及分类讨论等知识；本题综合性强，熟练掌握等腰三角形的性质和勾股定理，证明三角形全等是解本题的关键．