

2022年河北省唐山市路北区中考二模数学试题 (word版含答案)
展开2022年九年级第二次模拟检测
数学试卷
一、选择题(本大题共16个小题;1-10小题,每题3分;11-16小题,每题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列图形中,内角和与外角和相等的多边形是( )
A. B. C. D.
2.一个数用科学计数法表示为,则这个数是( )
A.5.01 B.0.501 C.0.0501 D.0.00501
3.几种气体的液化温度(标准大气压)如表:
气体 | 氧气 | 氢气 | 氮气 | 氦气 |
液化温度 | -183 | -253 | -195.8 | -268 |
其中液化温度最低的气体是( )
A.氦气 B.氮气 C.氢气 D.氧气
4.把多项式分解因式,结果正确的是( )
A. B.
C. D.
5.下列计算正确的是( )
A. B.
C. D.
6.某几何体的三视图如图所示,则该几何体是( )
A.圆柱 B.圆锥 C.三棱锥 D.三棱柱
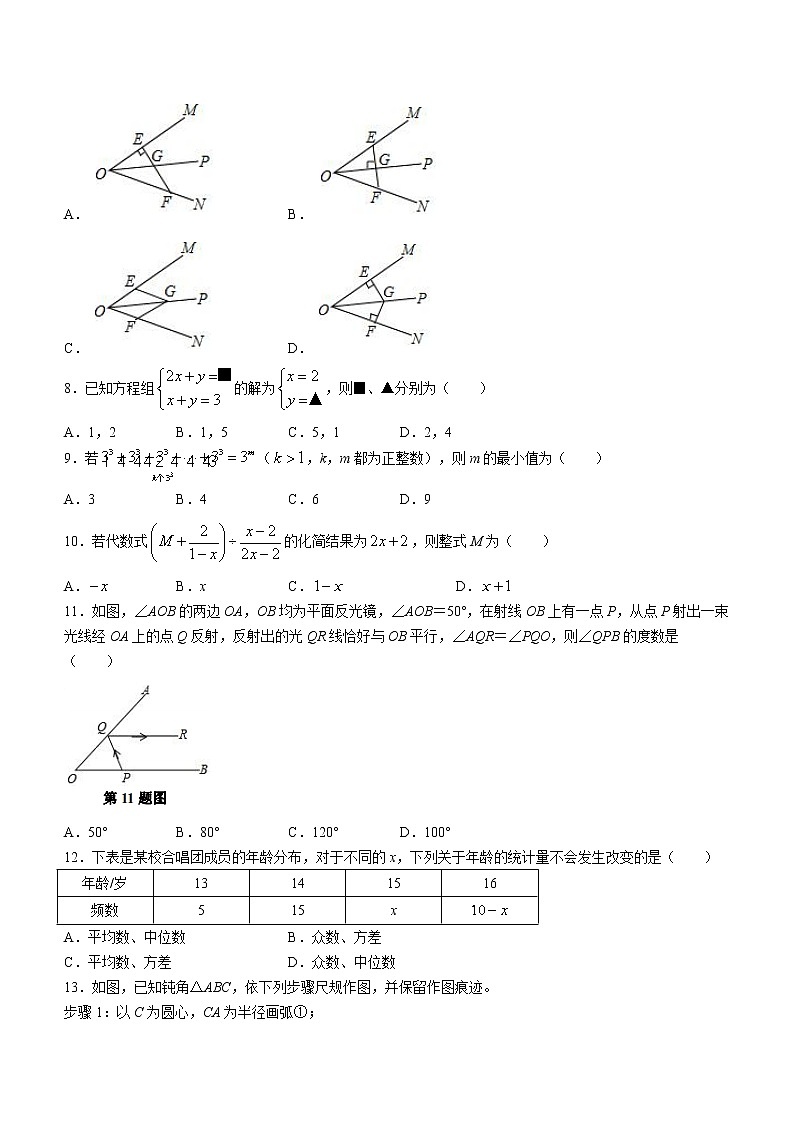
7.下列各图中,OP是∠MON的平分线,点E,F,G分别在射线OM,ON,OP上,则可以解释定理“角的平分线上的点到角的两边的距离相等”的图形是( )
A. B.
C. D.
8.已知方程组的解为,则■、▲分别为( )
A.1,2 B.1,5 C.5,1 D.2,4
9.若(,k,m都为正整数),则m的最小值为( )
A.3 B.4 C.6 D.9
10.若代数式的化简结果为,则整式M为( )
A. B.x C. D.
11.如图,∠AOB的两边OA,OB均为平面反光镜,∠AOB=50°,在射线OB上有一点P,从点P射出一束光线经OA上的点Q反射,反射出的光QR线恰好与OB平行,∠AQR=∠PQO,则∠QPB的度数是( )
A.50° B.80° C.120° D.100°
12.下表是某校合唱团成员的年龄分布,对于不同的x,下列关于年龄的统计量不会发生改变的是( )
年龄/岁 | 13 | 14 | 15 | 16 |
频数 | 5 | 15 | x |
A.平均数、中位数 B.众数、方差
C.平均数、方差 D.众数、中位数
13.如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹。
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②;
步骤3:连接AD,交BC延长线于点H。
下列叙述正确的是( )
A. B.AC平分∠BAD
C.BH垂直平分线段AD D.AB=AD
14.已知:四边形ABCD是平行四边形,如图所示.
求证:AO=CO,BO=DO.
以下是排乱的证明过程,正确的顺序应是( )
①∵∠ABO=∠CDO,∠BAC=∠DCA.
②∵四边形ABCD是平行四边形.
③∴,AB=DC.④△AOB≌△COD.⑤∴OA=OC,OB=OD
A.②①③④⑤ B.②③⑤①④
C.②③①④⑤ D.③②①④⑤
15.如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.5米,最高点C距灯柱的水平距离为1.6米,灯柱AB高为1.5米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为( )
A.3.2 B.0.32 C.2.5 D.1.6
16.如图,在△ABC中,∠B=∠C=40°,点D在线段BC上(不与B、C重合),若O为△ADC的内心,则∠AOC不可能是( )
A.100° B.120° C.140° D.150°
二、填空题(本大题共3个小题;每题2空,每空2分,共12分.)
17.如图1,点A,B,C是数轴上从左到右排列的三点,分别对应的数为,b,5.某同学将刻度尺如图2放置,使刻度尺上的数字0对齐数轴上的点A,发现点B对齐刻度尺1.5cm处,点C对齐刻度尺4.5cm处.
(1)在图1的数轴上,AC=________个单位长;
(2)求数轴上点B所对应的数b为________.
18.如图1,在△ABC内部任取一点,则图中互不重叠的所有角的和是540°
(1)在图1中的任一小三角形内任取一点(如图2),则图中互不重叠的所有角的和是______;
(2)以此类推,当取到点时,图中互不重叠的所有角的和是____________(用含n的代数式表示)
19.如图,在△ABC中,AB=8cm,AC=16cm,点P从A出发,以2cm/s的速度向B运动,同时点Q从C出发,以3cm/s的速度向A运动,当其中一个动点到达端点时,另一个动点也随之停止运动,设运动的时间为t.
(1)用含t的代数式表示:AQ________;
(2)当以A,P,Q为顶点的三角形与△ABC相似时,运动时间t=________.
三、解答题(本大题共7个小题;共66分)
20.本题8分
老师在黑板上出示了下面的5个未计算完的有理数.
,,,,
(1)求这5个数的和,并直接写出这5个数的中位数.
(2)在这5个数中,最大的数是m,最小的数是n.求的值.
21.本题9分
在化简题目中:◆表示+,-,×,÷四个运算符号中的某一个.
(1)若◆表示“-”,请化简
(2)当,时,的值为12,请推算出◆所表示的符号.
22.本题9分
为了解城镇民营企业员工每月的收入状况,统计局对全市城镇民营企业员工月平均收入随机抽样调查,将抽样的数据按“2000元以内”、“2000~4000元”、“4000~6000元”和“6000元以上”分为四组,进行整理,分别用A,B,C,D表示,得到下面两幅不完整的统计图.由图中所给出的信息解答下列问题:
(1)本次抽样调查的员工有_________人,在扇形统计图中x的值为_________,表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是_________;
(2)将不完整的条形统计图补充完整,并估计该市年城镇民营企业20万员工中,每月的收入在“2000~4000元”的约多少人?
(3)统计局根据抽样数据计算得到,该市城镇民营企业员工月平均收入为4872元,请你结合上述统计的数据,谈一谈用平均数反映月收入情况是否合理?
23.本题9分
如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2.
(1)求证:△AEC≌△BED;
(2)若∠C=75°,求∠AEB的度数;
(3)若∠AEC=90°,当△AEC的外心在直线DE上时,CE=2,求AE的长.
24.本题10分
如图,直线OC:与双曲线(x>0)交于点,且横坐标为1的点P也在双曲线(x>0)上,直线l经过点P,C.
(1)_________,_________;
(2)求直线l的解析式;
(3)设直线l与y轴交于点A,将直线OC沿射线CP方向平移至点A为止,直接写出直线OC在平移过程中与x轴交点横坐标的取值范围;
(4)直接写出直线l与双曲线(x>0)围成的区域内(图中阴影部分,不含边界)整点(横坐标和纵坐标都是整数)的坐标.
25.本题10分
如图,在矩形ABCD中,AD=4,∠BAC=30°,点O为对角线AC上的动点(不与A、C重合),以点O为圆心在AC下方作半径为2的半圆O,交AC于点E、F.
(1)求AC的长;
(2)当半圆O过点A时,求半圆O被AB边所截得的弓形的面积;
(3)若M为的中点,在半圆O移动的过程中,求BM的最小值;
(4)当半圆O与矩形ABCD的边相切时,直接写出AE的长.
26.本题12分
如图是某跳台滑雪训练场的横截面示意图,取水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系.图中的抛物线:近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4米处的A点滑出,滑出后沿一段抛物线:运动.
(1)当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线的函数解析式(不要求写出自变量x的取值范围);
(2)在(1)的条件下,当运动员运动水平线的水平距离为多少米时,运动员与小山坡的竖直距离为1米?
(3)当运动员运动到坡顶正上方,且与坡顶距离超过3米时,求b的取值范围.
2022年九年级第二次模拟检测数学参考答案
一、选择题(1-10小题,每题3分;11-16小题,每题2分,共42分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
答案 | C | C | A | A | C | B | D | C | B | B | D | D | C | C | A | A |
二、填空题:(每小题各有2个空,每空2分,共12分)
17.(1)9;(2);18.(1)900°;(2);19.(1),(2)或4s
三.解答题:(共67分)
20.解:(1),
中位数是1;
(2)∵最大的数是4,最小的数是,
∴
21.解:(1)
(2)由题意得,
即
所以◆表示÷.
22.解:(1)500,14,21.6°;
(2)补统计图如图;
每月的收入在“2000~4000元”的约有:(万人);
(3)不合理,因为平均数不能代表大多数人的收入,应该用中位数或众数代表.
23.证明:(1)∵∠ADE=∠1+∠C=∠2+∠BDE,且1=2,∴∠C=∠BDE,
∵∠A=∠B,AE=BE,∴△AEC≌△BED;
(2)∵△AEC≌△BED,∴DE=EC,∠BDE=∠AEC,
∴∠EDC=∠C=75°,∴∠1=30°,∴∠AEB=∠1=30°;
(3)∵∠AEC=90°,△AEC的外心在直线DE上,
∴点D是AC的中点,∴AD=CD=DE,
∵DE=EC,∴△ECD是等边三角形,
∴∠C=60°,∴
24.解:(1),3;
(2)由(1)可得双曲线,
将代入得,∴,
设直线l解析式为,则,解得,
∴直线l解析式为;
(3)交点横坐标的取值范围是;
(4)如图:整点的坐标是、.
25.解:(1)∵AD=4,∠BAC=30°,∴AC=8;
(2)如图,当半圆O过点A时,设该半圆与AB的另一个交点为点G,连接OG,过点O作ON⊥AB于点N
∵OA=OG=2,∠BAC=30°,
∴ON=1,,∠OGA=30°,∴∠AOG=120°
∴,.
∴
(3)如图,连接OM,BM,
当O、B、M三点共线时,BM的值最小,此时OB⊥AC.
∵AD=BC=4,∠BAC=30°,∴.∴.
∴;
(4)当半圆O与矩形的边相切时,AE的长为2或
26.(1)根据题意可知:点,点代入抛物线:得,
,解得:,
∴抛物线的函数解析式;
(2)∵运动员与小山坡的竖直距离为1米,
∴,
解得:(不合题意,舍去),,
故当运动员运动水平线的水平距离为12米时,运动员与小山坡的竖直距离为1米;
(3)∵点,∴抛物线:,
∴抛物线:,∴坡顶坐标为,
∵当运动员运动到坡顶正上方,且与坡顶距离超过3米时,
∴,解得:.
2024年河北省唐山市路北区中考二模前数学摸底试题: 这是一份2024年河北省唐山市路北区中考二模前数学摸底试题,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年河北省唐山市路北区中考数学二模试卷(含解析): 这是一份2023年河北省唐山市路北区中考数学二模试卷(含解析),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年河北省唐山市路北区中考二模数学试题(含解析): 这是一份2023年河北省唐山市路北区中考二模数学试题(含解析),共27页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












