2022年安徽省城名校中考最后三模数学试题（三） (word版含答案)

省城名校2022年中考最后三模（三）

数学试题

一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A、B、C、D四个选项，其中只有一个是正确的。

1．的绝对值是（    ）

A． B． C． D．

2．计算的结果是（    ）

A． B． C． D．

3．“工”字型零件如图所示，其左视图是（    ）

A． B． C． D．

4．新华社北京5月5日电，记者从国家邮政局获悉，“五一”假期全国邮政快递业揽收快递包裹13.4亿件，同比增长2.3%，其中“13.4亿”用科学记数法表示为（    ）

A． B． C． D．

5．化简的结果是（    ）

A． B． C． D．

6．如图，AB为的直径，点C，D在上．若，则的度数是（    ）

A．15° B．20° C．25° D．30°

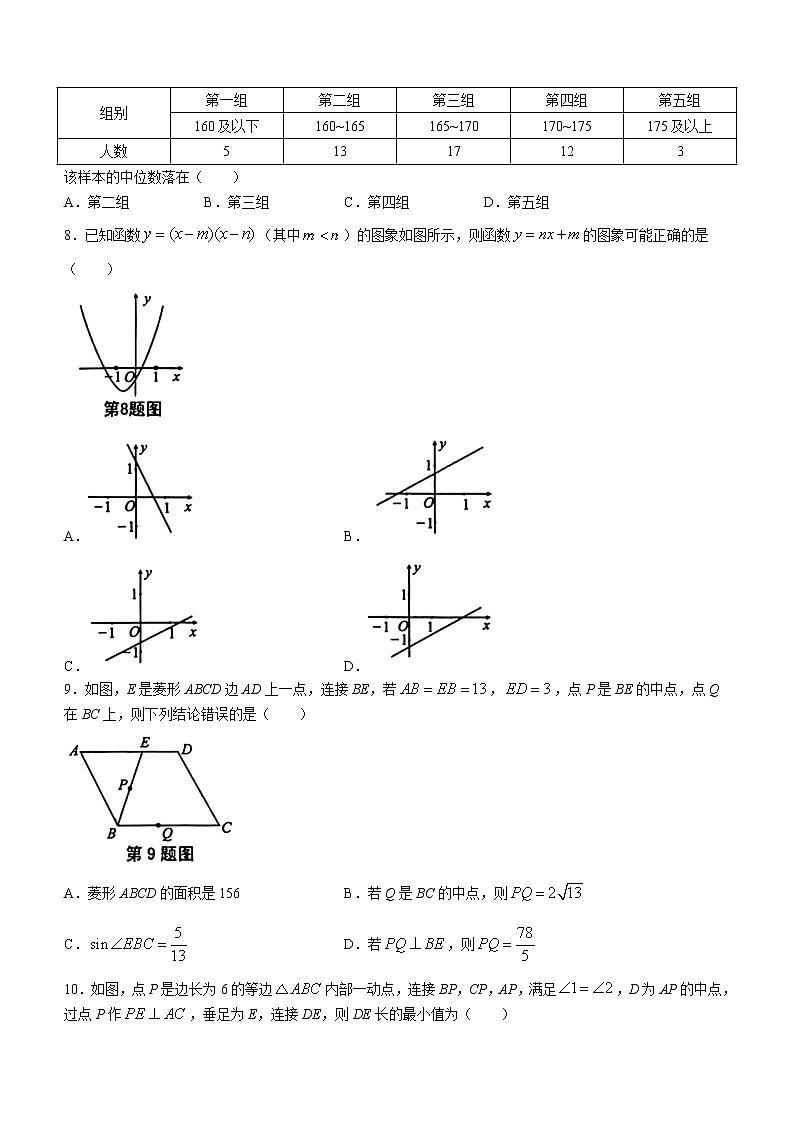
7．为了解九年级男生的身高情况，校体育部随机抽测了九年级部分男生的身高（单位：厘米），数据统计如下：

该样本的中位数落在（    ）

A．第二组 B．第三组 C．第四组 D．第五组

8．已知函数（其中）的图象如图所示，则函数的图象可能正确的是（    ）

A．  B．

C．  D．

9．如图，E是菱形ABCD边AD上一点，连接BE，若，，点P是BE的中点，点Q在BC上，则下列结论错误的是（    ）

A．菱形ABCD的面积是156 B．若Q是BC的中点，则

C．  D．若，则

10．如图，点P是边长为6的等边内部一动点，连接BP，CP，AP，满足，D为AP的中点，过点P作，垂足为E，连接DE，则DE长的最小值为（    ）

A．2 B． C．3 D．

二、填空题（本大题共4小题，每小题5分，满分20分）

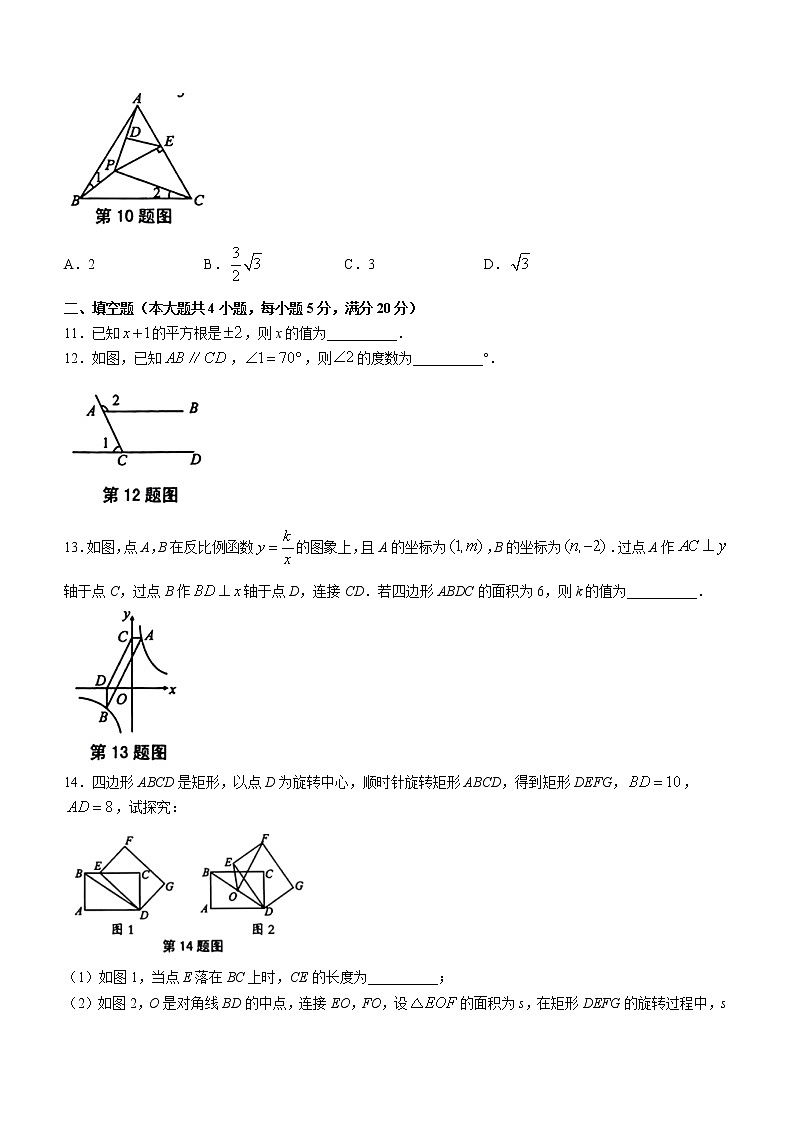
11．已知的平方根是，则x的值为__________．

12．如图，已知，，则的度数为__________°．

13．如图，点A，B在反比例函数的图象上，且A的坐标为，B的坐标为．过点A作轴于点C，过点B作轴于点D，连接CD．若四边形ABDC的面积为6，则k的值为__________．

14．四边形ABCD是矩形，以点D为旋转中心，顺时针旋转矩形ABCD，得到矩形DEFG，，，试探究：

（1）如图1，当点E落在BC上时，CE的长度为__________；

（2）如图2，O是对角线BD的中点，连接EO，FO，设的面积为s，在矩形DEFG的旋转过程中，s的取值范围为__________．

三、（本大题共2小题，每小题8分，满分16分）

15．解不等式：．

16．如图，在每个小正方形的边长为1个单位的网格中，点A，B，C均是格点（网格线的交点）．

（1）在图中将平移得到，使得点B的对应点为点C，作出平移后的图形；

（2）用无刻度直尺在图中的线段AB上找一点P，使．

四、（本大题共2小题，每小题8分，满分16分）

17．某商店以每盏25元的价格采购了一批节能灯，运输过程中损坏了3盏，然后以每盏30元售完，共获利160元．该商店共购进了多少盏节能灯？

18．杨辉三角是中国古代数学杰出的研究成果之一．如图所示是一种变异的“杨辉三角”：

仔细观察上表，根据你发现的规律，解答下列问题：

（1）从上往下数第6行，左边第二个数是__________，右边最后一个数是__________；

（2）该数表中是否存在数255？并说明理由．

五、（本大题共2小题，每小题10分，满分20分）

19．如图，在东西方向的旅游线路上设有两个公交站点A，B，它们相距4.9千米，景点C在B的南偏东23°方向，且千米；景点D在A的正南方向，且在C的北偏东67°方向．求景点D到线路AB的距离．（参考数据：，，）

20．如图，在四边形ABCD中，，，以BC为直径的半与边AD相切于点E．

（1）求证：；

（2）若，求DE的长．

六、（本题满分12分）

21．晴明中学为培养学生正确的劳动价值观和良好的劳动品质，特开设了A农业园艺、B家禽饲养、C营养烹饪、D家电维修等四项特色劳动课程，学校要求每名学生必须选修且只能选修一项课程．为保证课程的有效实施，学校随机对部分学生选择课程情况进行了一次调查，并将调查结果绘制成如下不完整的统计图．

根据以上信息，解答下列问题：

（1）学校这次调查共抽取__________人，补全条形统计图；

（2）该校有1000名学生，请你估计选择“A”课程的学生有多少名；

（3）在劳动课程中表现优异的明明和兰兰两位同学被选中与其他学生一起参加劳动技能展示表演，展示表演分为3个小组，求明明和兰兰两人恰好分在同一组的概率．

七、（本题满分12分）

22．已知抛物线（a是实数）．

（1）若该当抛物线的顶点的纵坐标为，求该抛物线的表达式；

（2）若点，都在该抛物线上，求b的最大值．

八、（本题满分14分）

23．如图1，在中，，，点D是AC的中点，点E在BC上，连接AE交BD于F，作交AC于G，连接BG，BG交AE于P．

（1）求的大小；

（2）连接CP并延长交AB于点K，如图2，若K恰好是AB的中点．

①求证：；②直接写出的值．

省城名校2022年中考最后三模（三）

数学试题参考答案及评分标准

一、选择题（本大题共10小题，每小题4分，满分40分）

10．D  在中，，易得，故点P在的外接圆的弧BC上，当时，AP有最小值，则DE的最小值是．

二、填空题（本大题共4小题，每小题5分，满分20分）

11．3 12．110

13．5

连接AD，延长AC，BD交于点E，点B的坐标为，

则点A的坐标为，∵轴，轴，

∴，，

，

∵四边形ABDC的面积为6，∴，

∴，∴．

14．（1） （2）

（1），当点E落在BC上时，

CE的长度为；

（2）当点E落在BD上时，s最小，此时，，

∴；

当点D落在BD的反向延长线上时，s最大，，

∴，∴．

三、（本大题共2小题，每小题8分，满分16分）

15．解：去分母得，

移项得，

合并同类项得，

系数化为1得．

16．解：

（1）如图所示；．

（2）点P如图所示．

四、（本大题共2小题，每小题8分，满分16分）

17．解：设该商店共购进了x盏节能灯，

得，解得，

答：该商店共购进了50盏节能灯．

18．解：

（1）64，68；

（2）该数表中存在数255；

理由：经观察发现数表中的第n行数字从左到右依次为、、、……、，假设255分布在第n行，则，可得，即，故255位于第8行左起第1个数．

五、（本大题共2小题，每小题10分，满分20分）

19．解：如图，过点C作交于点M，过点D作于点N．

∵景点D在A的正南方向，∴，∴四边形MADN为矩形，

∴，；

在中，，千米，

由得（千米），

∴千米，∴千米；

由得（千米）；

在中，，

由得（千米），

∴千米，∴千米，

即景点D到线路AB的距离为5千米．

20．解：

（1）如图，连接OE，∵半与AD相切于点E，∴．

∵，∴，∴，∴．

∵，∴，∴；

（2）如图，连接BE，∵，，∴，

∵，∴．

设，则，∵BC为的直径，∴．

∵，

∴，，

∴，∴，∴，即，

解得，即DE的长为．

六、（本题满分12分）

21．解：

（1）200；（由条形图和扇形统计图可知：选择C的人数为56人，所占的百分比为28%，

∴（人），选择D的学生人数为：（人））

补全条形统计图如下：

（2）（人），∴选择“A”课程的学生大约有320人．

（3）画树状图如图（3个小组记为A，B，C）：

可得一共有9种可能，明明和兰兰两人恰好分在同一组有3种，所以明明和兰兰两人恰好分在同一组的概率为．

七、（本题满分12分）

22．解：

（1）∵抛物线，∴，

∴，∴该抛物线的表达式为；

（2）点，都在该抛物线上，

∴对称轴为直线，

∴，∴，∴点N的坐标为，

代入，得，

∴当时，b有最大值，最大值为3．

八、（本题满分14分）

23．解：

（1）证明：∵，，∴，∵D是AC的中点，

∴，，．∵，

∴，∴，∴．∵，

∴．在与中，，

∴，

∴．∵，，

∴，故．

（2）①∵，，∴，，

∴．∵，K恰好是AB的中点，∴，

∴．

又∵，∴．∵，∴，

∴，即，

过点C作交BG的延长线于点H，∴．

在与中，，∴，∴．

∵，∴．∵，∴，

∴；

（也可设，则，，可证，得

，∴，又可证，

∴，∴，

∴，∴．）

②．

（简析：由得，∵，

∴．∵，∴，

∴．）