2022年江苏省无锡市中考数学仿真模拟试卷(word版含答案)

这是一份2022年江苏省无锡市中考数学仿真模拟试卷(word版含答案)，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022年中考数学江苏省无锡市仿真模拟试卷题号一二三总分得分    注意：本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题，所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题，所有答案必须填在答题卷的相应位置。答案写在试卷上均无效，不予记分。 一、选择题（本大题共10小题，共30分）下列说法：①相反数等于本身的数是0；②绝对值等于本身的是正数；③倒数等于本身的数是±1； ④平方等于本身的数是0和1；⑤平方为9的数是3；⑥有绝对值最小的有理数．正确的个数为（　　）A.  B.  C.  D. 汽车由北京驶往相距120千米的天津，它的平均速度是40千米/时，则汽车距天津的路程s（千米）与行驶时间t（时）的函数关系及自变量的取值范围是（　　）A.  B.
C.  D. 下列各式计算正确的是（　　）A.  B.  C.  D. 小明有两根长度分别为5cm和8cm的木棒，他想钉一个三角形的木框．现在有5根木棒供他选择，其长度分别为3cm、5cm、10cm、13cm、14cm．小明随手拿了一根，恰好能够组成一个三角形的概率为（）A.  B.  C.  D. 一组数据为5，6，7，8，10，10，某同学在抄题时，误把其中一个10抄成了100，那么该同学所抄的数据和原数据相比，不变的统计量是（　　）A. 中位数 B. 平均数 C. 方差 D. 众数下列几何体中，主视图是矩形的是（　　）A.  B.  C.  D. 菱形具有而矩形不一定具有的特征是（　　）A. 四条边相等 B. 四个内角都相等 C. 对角线互相平分 D. 两组对边分别平行如图，AB为⊙O的直径，点C，D是⊙O上的两点，连接CA，CD，AD，若∠CDA=120°，AB=4，则长是（　　）A.
B.
C.
D. 如图，一次函数与反比例函数的图象相交于A、B两点，则图中使反比例函数的值小于一次函数的值的x的取值范围是() A.
B.
C. ，或
D. ，或
 已知，等腰Rt△ABC中AC=BC，点D在BC上，且∠ADB=105°，ED⊥AB，G是AF延长线上一点，BE交AG于F，且DE=2FG，连GE、GB．则下列结论：
①AG⊥BE；②∠DGE=60°；③BF=2FG；④AD+DC=AB．
其中正确的结论有（　　）A.
B.
C.
D.  二、填空题（本大题共8小题，共24分）-2×4的相反数是______ ；的算术平方根是______ .据有关部门统计，全国现有党员人数已突破83000000人，将数据83000000用科学记数法表示为           ．分解因式2x2﹣4x+2＝____．已知圆锥的底面半径为2cm，母线长为6cm（如图），则圆锥的侧面展开图的圆心角为______ 度.

  若二次函数y=ax2的图象开口向上，则直线y=ax+a不经过第______ 象限．如图在Rt△ABC中，∠ACB=90°，CD⊥AB于D，若AC=6，BC=8，则CD=______．

  如图，在▱ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F，若△EDF的周长为9，则△BCF的周长为______ ．


  如图，正方形ABCD边长为2，E为CD的中点，以点A为中心，把△ADE顺时针旋转90°得△ABF，连接EF，则EF的长等于______ ．

    三、解答题（本大题共10小题，共96分）解关于x的方程：（x+2）2-（x-2）（x+2）=6．观察下列等式：
，，，…
解答下列问题：
（1）若n为正整数，请你根据上述规律写出第n个式子．
（2）利用规律解方程：
=．如图，▱ABCD中，E是AD边的中点，BE的延长线与CD的延长线相交于F.
（1）求证：△ABE≌△DFE.
（2）连接AF、BD，若三角形DEF的面积为1，则四边形ABCF的面积为多少.
  为体现我们党和国家对治理污染紧迫性和艰巨性的清醒认识，倡导全社会共同行动，保卫我们赖以生存的共同家园．达州市某校举行了“洁美家园”的演讲比赛，赛后整理参赛同学的成绩，将学生的成绩分成 A、B、C、D四个等级，并制成了如下的条形统计图和扇形统计图（如图1、图2）
（1）补全条形统计图；
（2）学校决定从本次比赛中获得A和B的学生中各选出一名去参加市中学生环保演讲比赛，已知A等中男生有2名，B等中女生有3名，请你用“列表法”或“树状图法”的方法求出所选两位同学恰好是一名男生和一名女生的概率．
为了丰富同学们的课余生活，某学校将举行“亲近大自然”户外活动．现随机抽取了部分学生进行主题为“你最想去的景点是”的问卷调查，要求学生只能从“A（绿博园），B（人民公园），C（湿地公园），D（森林公园）”四个景点中选择一项，根据调查结果，绘制了如下两幅不完整的统计图．
（1）本次共调查了多少名学生？
（2）补全条形统计图；
（3）若该学校共有3 600名学生，试估计该校最想去湿地公园的学生人数．
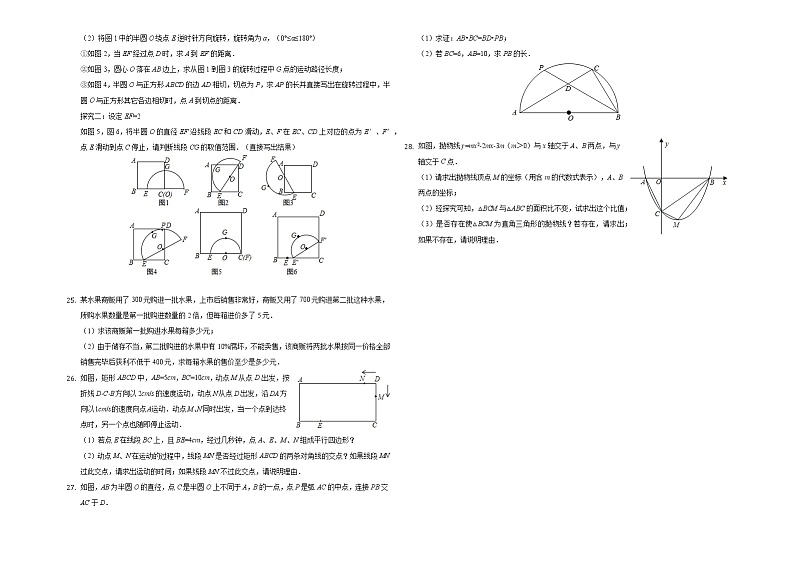
四边形ABCD是正方形，BC=3，点E在BC上且BE=1，以EF为直径作半圆O，点G是半圆弧的中点
探究一：设定EF=4，
（1）如图1，当F在BC延长线上时，DG的长______；
（2）将图1中的半圆O绕点E逆时针方向旋转，旋转角为a，（0°≤α≤180°）
①如图2，当EF经过点D时，求A到EF的距离．
②如图3，圆心O落在AB边上，求从图1到图3的旋转过程中G点的运动路径长度；
③如图4，半圆O与正方形ABCD的边AD相切，切点为P，求AP的长并直接写出在旋转过程中，半圆O与正方形其它各边相切时，点A到切点的距离．
探究二：设定EF=2
如图5，图6，将半圆O的直径EF沿线段EC和CD滑动，E、F在EC、CD上对应的点为E′、F′，点E滑动到点C停止，请判断线段CG的取值范围．（直接写出结果）
某水果商贩用了300元购进一批水果，上市后销售非常好，商贩又用了700元购进第二批这种水果，所购水果数量是第一批购进数量的2倍，但每箱进价多了5元．
（1）求该商贩第一批购进水果每箱多少元；
（2）由于储存不当，第二批购进的水果中有10%腐坏，不能卖售，该商贩将两批水果按同一价格全部销售完毕后获利不低于400元，求每箱水果的售价至少是多少元．如图，矩形ABCD中，AB=5cm，BC=10cm，动点M从点D出发，按折线D-C-B方向以2cm/s的速度运动，动点N从点D出发，沿DA方向以1cm/s的速度向点A运动．动点M、N同时出发，当一个点到达终点时，另一个点也随即停止运动．
（1）若点E在线段BC上，且BE=4cm，经过几秒钟，点A、E、M、N组成平行四边形？
（2）动点M、N在运动的过程中，线段MN是否经过矩形ABCD的两条对角线的交点？如果线段MN过此交点，请求出运动的时间；如果线段MN不过此交点，请说明理由．如图，AB为半圆O的直径，点C是半圆O上不同于A，B的一点，点P是弧AC的中点，连接PB交AC于D．
（1）求证：AB•BC=BD•PB；
（2）若BC=6，AB=10，求PB的长．
如图，抛物线y=mx2-2mx-3m（m＞0）与x轴交于A、B两点，与y轴交于C点．
（1）请求出抛物线顶点M的坐标（用含m的代数式表示），A、B两点的坐标；
（2）经探究可知，△BCM与△ABC的面积比不变，试求出这个比值；
（3）是否存在使△BCM为直角三角形的抛物线？若存在，请求出；如果不存在，请说明理由．

  
 1.D2.A3.A4.A5.A6.D7.A8.B9.D10.B11.8 12.8.3×10713.2（x-1）214.12015.四16.4.817.1818.19.解：（x+2）2-（x-2）（x+2）=6，
x2+4x+4-x2+4=6，
4x=6-8，
x=-．20.解：（1）根据题意得：=-；

（2）原方程可化为：-+-+-+-=，
即-==，
去分母得：3x+10=4，
解得：x=-2，
经检验x=-2是增根，分式方程无解．21.（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=DC，
∴∠F=∠EBA，
∵E是AD边的中点，
∴DE=AE，
在△ABE与△DFE中，
，
∴△ABE≌△DFE（AAS）；

（2）解：∵△ABE≌△DFE，
∴DF=AB，
∵AB∥CD，
∴四边形ABDF是平行四边形，
∵三角形DEF的面积为1，
∴S▱ABCD=4S△DEF=4，
∴S△BCD=S▱ABCD=×4=2，
∴S四边形ABDF=S▱ABDF+S△BCD=4+2=6．22.解：（1）根据题意得：3÷15%=20（人），
故等级B的人数为20-（3+8+4）=5（人），
补全统计图，如图所示；

（2）列表如下： 男男女女女男（男，男）（男，男）（女，男）（女，男）（女，男）男（男，男）（男，男）（女，男）（女，男）（女，男）女（男，女）（男，女）（女，女）（女，女）（女，女）所有等可能的结果有15种，其中恰好是一名男生和一名女生的情况有8种，
则P恰好是一名男生和一名女生=．23.解：（1）本次调查的样本容量是15÷25%=60；
（2）选择C的人数为：60-15-10-12=23（人），
补全条形图如图：

（3）×3600=1380（人）．
答：估计该校最想去湿地公园的学生人数约由1380人．24.125.解：（1）设该商场第一批购进了这种水果x箱，则第二批购进这种水果2x箱，
可得：-=5，
解得：x=10，
经检验：x=10是原分式方程的解，
=30（元），
答：该商贩第一批购进水果每箱30元；
（2）设水果的售价为y元，根据题意得：
30y-（300+700）-20×10%y≥400，
解得：y≥50，
则水果的售价为50元．
答：每箱水果的售价至少为50元．26.解：（1）∵点N只在AD上运动，
∴当点M运动到BC边上的时候，点A、E、M、N才可能组成平行四边形，
即2.5＜t＜7.5，
设经过t秒，四点可组成平行四边形．分两种情形：
①当M点在E点右侧，
如图：此时AN=EM，则四边形AEMN是平行四边形，
∵DN=t，CM=2t-5，
∴AN=10-t，EM=10-4-（2t-5），
∴10-t=10-4-（2t-5），
解得：t=1，
∵2.5＜t＜7.5，
∴t=1舍去，
②当M点在B点与E点之间，如图，
则MC=2t-5，BM=10-（2t-5）=15-2t，
∴ME=4-（15-2t）=2t-11，
2t-11=10-t，解得t=7，此时符合，
∴当t=7秒时，点A、E、M、N组成平行四边形；
（2）动点M、N在运动的过程中，线段MN能经过矩形ABCD的两条对角线的交点，此时M在BC上，如图，
∵四边形ABCD是矩形，
∴OA=OC，AD∥BC，
∴∠NAO=∠MCO，
在△ANO和△CMO中
∴△ANO≌△CMO（ASA），
∴AN=CM，
设N运动的时间是t秒，则10-t=2t-5，
解得：t=5，
即动点M、N在运动的过程中，线段MN能经过矩形ABCD的两条对角线的交点，此时运动的时间是5秒．27.（1）证明：如图，连接AP，
∵AB为半圆O的直径，
∴∠APB=∠ACB=90°，
∵点P是弧AC的中点，
∴∠CBD=∠ABP，
∴△ABP∽△DBC，
∴AB•BC=BD•PB；

（2）解：连接OP，OP交AC于E点，
在直角△ABC中，BC=6，AB=10，
∴AC==8，
∵点P是弧AC的中点，
∴OP⊥AC，AE=4，
由三角形中位线定理得OE=BC=3，
∴PE=5-3=2，
在直角△APE中，AP==2，
在直角△ABP中，PB==4．28.解：（1）∵y=mx2-2mx-3m=m（x2-2x-3）=m（x-1）2-4m，
∴抛物线顶点M的坐标为（1，-4m）；
∵抛物线y=mx2-2mx-3m（m＞0）与x轴交于A、B两点，
∴当y=0时，mx2-2mx-3m=0，
∵m＞0，
∴x2-2x-3=0；
解得x1=-1，x2=3，
∴A、B两点的坐标为（-1，0）、（3，0）．

（2）当x=0时，y=-3m，
∴点C的坐标为（0，-3m）．
∴．
过点M作MD⊥x轴于点D，则OD=1，BD=OB-OD=2，
MD=|-4m|=4m．
∴S△BCM=S△BDM+S梯形OCMD-S△OBC
=
=
=3m．
∴S△BCM：S△ABC=1：2，
故答案为：；

（3）存在使△BCM为直角三角形的抛物线；
过点C作CN⊥DM于点N，则△CMN为Rt△，CN=OD=1，DN=OC=3m，
∴MN=DM-DN=m．
∴CM2=CN2+MN2=1+m2；
在Rt△OBC中，BC2=OB2+OC2=9+9m2，
在Rt△BDM中，BM2=BD2+DM2=4+16m2；
①如果△BCM是Rt△，且∠BMC=90°，那么CM2+BM2=BC2，
即1+m2+4+16m2=9+9m2，
解得，
∵m＞0，∴．
∴存在抛物线y=x2-x-使得△BCM是Rt△；
②如果△BCM是Rt△，且∠BCM=90°，那么BC2+CM2=BM2，
即9+9m2+1+m2=4+16m2，
解得m=±1，
∵m＞0，
∴m=1；
∴存在抛物线y=x2-2x-3，使得△BCM是Rt△；
③如果△BCM是Rt△，且∠CBM=90°，那么BC2+BM2=CM2，
即9+9m2+4+16m2=1+m2，整理得，此方程无解；
∴以∠CBM为直角的直角三角形不存在；
综上所述，存在抛物线y=x2-x-和y=x2-2x-3，使得△BCM是直角三角形．