苏科版九年级上册2.6 正多边形与圆教学设计及反思

2.6  正多边形与圆                                           

教学目标：

1、了解正多边形的概念、正多边形和圆的关系；

2、会通过等分圆心角的方法等分圆周，画出所需的正多边形；

3、能够用直尺和圆规作图，作出一些特殊的正多边形。

教学重点、难点：

重点：正多边形的概念及正多边形与圆的关系

难点：利用直尺与圆规作特殊的正多边形

教学过程：

一、情境创设

观察下列图形，你能说出这些图形的特征吗？

二、探索活动

活动一:观察生活中的一些图形，归纳它们的共同特征，引入正多边形的概念

_________________________________的多边形叫做正多边形。

（注：各边相等与各角相等必须同时成立，否则不一定是正多边形，例如菱形、矩形等）

活动二:用量角器作正多边形，探索正多边形与圆的内在联系

1、用量角器将一个圆n（n≥3）等分，依次连接各等分点所得的n边形是这个圆的____________；圆的内接正n边形将圆______________；

2、__________________________叫正多边形的中心。

活动三:探索正多边形的对称性

正三角形、正方形、正五边形、正六边形、正八边形中，哪些是轴对称图形？哪些是中心对称图形？哪些既是轴对称图形，又是中心对称图形？如果是轴对称图形，画出它的对称轴；如果是中心对称图形，找出它的对称中心。

结论：

正n(n为奇数)边形是_________图形，有____条对称轴，其对称轴是___________________；

正n(n为偶数)边形既是_______图形又是___________；有______条对称轴，其对称轴是____________________________________________；其对称中心是___________。

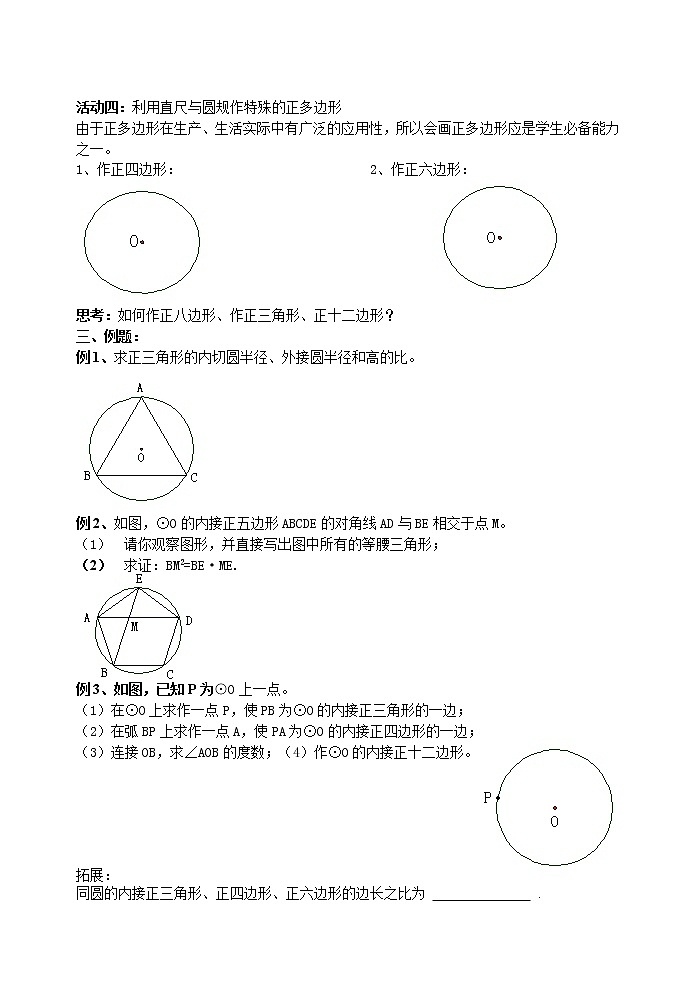
活动四：利用直尺与圆规作特殊的正多边形

由于正多边形在生产、生活实际中有广泛的应用性，所以会画正多边形应是学生必备能力之一。

1、作正四边形：                           2、作正六边形：

思考：如何作正八边形、作正三角形、正十二边形？

三、例题：

例1、求正三角形的内切圆半径、外接圆半径和高的比。

例2、如图，⊙O的内接正五边形ABCDE的对角线AD与BE相交于点M。

（1）       请你观察图形，并直接写出图中所有的等腰三角形；

（2）          求证：BM2=BE·ME.

例3、如图，已知P为⊙O上一点。

（1）在⊙O上求作一点P，使PB为⊙O的内接正三角形的一边；

（2）在弧BP上求作一点A，使PA为⊙O的内接正四边形的一边；

（3）连接OB，求∠AOB的度数；（4）作⊙O的内接正十二边形。

拓展：

同圆的内接正三角形、正四边形、正六边形的边长之比为                .

四、课堂小结

五、课堂作业

1、下列命题中，正确的说法有_________________（填序号）。

①正多边形的各边相等；②各边相等的多边形是正多边形；③正多边形的各角相等；④各角相等的多边形是正多边形；⑤既是轴对称图形，又是中心对称的多边形是正多边形。

2、用量角器将圆五等分，得到正五边形ABCDE（如图），

AC、BD相交于点P，则∠APB等于________。

3、如果要画一个正十二边形，那么用量角器将圆_______等分，

   每一份的圆心角是_______°。

4、用圆规和直尺在下列圆中画正三角形、正八边形。

5、如图，在半径为10cm的⊙O中作一个正六边形ABCDEF.试求此正六边形的面积。

6、如图1、2、3、4，M、N分别为⊙O的内接正三角形ABC，正四边形ABCD、正五边形ABCDE，……正n边形ABCDE……的边AB、BC上的点，且BM=CN，连接OM、ON。

（1）求图1中∠MON的度数；（2）图2中∠MON的度数为_________；

（3）请探究∠MON的度数与正n边形边数n的关系（直接写答案）。

课后作业：

1.判断

(1)各边相等的多边形是正多边形.（       ）

(2)各角相等的多边形是正多边形.（       ）

(3)正十边形绕其中心旋转36°和本身重合.（       ）

2.正多边形都是     对称图形，一个正n边形有    条对称轴，每条对称轴都通过正n边形的  ；一个正多边形，如果有偶数条边，那么它既是      ，又是           对称图形。

3.正十二边形的每一个外角为    °每一个内角是     °该图形绕其中心至少旋

转    °和本身重合.

4.用一张圆形纸剪一个边长为4cm的正六边形，则这个圆形纸片半径最小应为_   cm.

5.正方形ABCD的外接圆圆心O叫做正方形ABCD的______．

6.正方形ABCD的内切圆⊙O的半径OE叫做正方形ABCD的______．

7.若正六边形的边长为1，那么正六边形的中心角是______度，半径是______，边心距是______，它的每一个内角是______．

8.正n边形的一个外角度数与它的______角的度数相等．

9、⊙的内接多边形周长为3 ，⊙的外切多边形周长为3.4，则下列各数中与此圆的周长最接近的是（     ）A．          B．         C．        D．

10、粉笔是校园中最常见的必备品．图1是一盒刚打开的六角形粉笔，总支数为50支．图2是它的横截面（矩形ABCD），已知每支粉笔的直径为12mm，由此估算矩形ABCD的周长约为_______ mm．(，结果精确到1 mm)             

11、如图，AB为半圆的直径，C是半圆弧上一点，正方形DEFG的一边DG在直径AB上，另一边DE过ΔABC的内切圆圆心O，且点E在半圆弧上。①若正方形的顶点F也在半圆弧上，则半圆的半径与正方形边长的比是______________；②若正方形DEFG的面积为100，且ΔABC的内切圆半径=4，则半圆的直径AB = __________.

12、如图①，在平面直角坐标系xOy中，点M在x轴的正半轴上，⊙M交x轴于A、B两点，交y轴于C、D两点，且C为弧AE的中点，AE交y 轴于G点，若点A的坐标为（－2，0），AE=8．  

（1）求点C的坐标；（2）连接MG、BC，试说明：MG∥BC；

（3）如图2，过点D，作⊙M的切线，交x轴于点P，动点F在⊙M的圆周上运动时，OF/PF的比值是否发生变化，若不变，求出比值；若改变，说明变化规律．