








高中数学人教A版 (2019)必修 第一册2.2 基本不等式优秀ppt课件
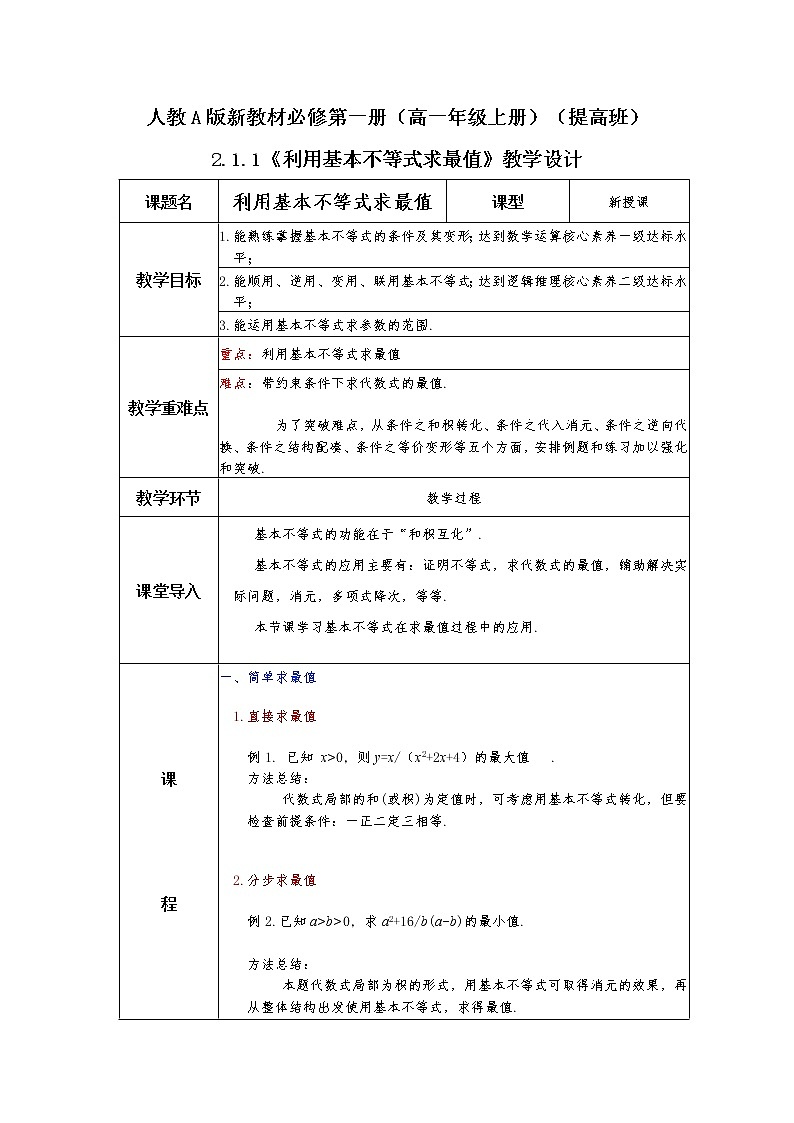
展开基本不等式的功能在于“和积互化”. 基本不等式的应用主要有:证明不等式,求代数式的最值,辅助解决实际问题,消元,多项式降次,等等. 本节课学习基本不等式在求最值过程中的应用.
用基本不等式求最值
(一) 直接求最值
方法总结: 代数式局部的和(或积)为定值时,可考虑用基本不等式转化,但要检查前提条件:一正二定三相等.
(二) 分步求最值
方法总结: 本题代数式局部为积的形式,用基本不等式可取得消元的效果,再从整体结构出发使用基本不等式,求得最值.
例3. 已知 x>0, y>0 ,x+y+2=xy,则xy的 最小值为 .
(三) 条件最值之和积转化
方法总结: 已知条件同时含有和与积,而目标式只含有积,故先借助于基本不等式将和转化为积,再求最值.
已知 x>0, y>0, 且x2+4y2+5xy=1,则 x+2y 的最小值为 .
(四) 条件最值之代入消元
(五) 条件最值之逆向代换
方法总结: 在求含两个变量代数式的最值时,代入消元是可考虑的一个方向;如果条件是代数式等于常数的结构,逆向代换往往是高效的解决途径.
(四) 配凑条件求最值
(六) 条件最值之结构配凑
方法总结: 用逆向代换时,代数式结构不完整的,可以进行适当的配凑. 本题也可以先用代入消元法,再用基本不等式.
(七) 条件最值之等价变形
方法总结: 条件式应该怎样使用,取决于目标式的结构特点. 本题目标式为积的形式,故先将条件式变形,化归为“和化积”模型. 但如果问题是“求x+2y的最小值”,则条件式无需变形,只需逆向代换即可.
逆向代换
结构配凑
等价变形
二、本节课提升的核心素养
三、本节课训练的数学思想方法
基础作业: .
能力作业: .
人教A版 (2019)必修 第一册2.2 基本不等式教课内容课件ppt: 这是一份人教A版 (2019)必修 第一册2.2 基本不等式教课内容课件ppt,共38页。PPT课件主要包含了目标认知,两个重要不等式,知识点一基本不等式,不小于,知识点二最值定理,①②③等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.2 基本不等式精品课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.2 基本不等式精品课件ppt,文件包含22课件环节四基本不等式二pptx、22教案环节四基本不等式二doc、22同步测试环节四基本不等式二doc等3份课件配套教学资源,其中PPT共11页, 欢迎下载使用。
人教A版 (2019)必修 第一册4.2 指数函数试讲课课件ppt: 这是一份人教A版 (2019)必修 第一册4.2 指数函数试讲课课件ppt,文件包含新人教A版数学必修第一册第4章+22指数函数第二课时提高班课件pptx、新人教A版数学必修第一册第4章+22指数函数第二课时提高班教案docx等2份课件配套教学资源,其中PPT共29页, 欢迎下载使用。














