北师大版八年级下册数学 期末考试检测试卷

这是一份北师大版八年级下册数学 期末考试检测试卷，共15页。试卷主要包含了若a＞b，则下列不等式成立的是，在平面直角坐标系中，已知点O，若分式方程有增根，则m等于等内容，欢迎下载使用。
北师大版八年级下册数学 期末考试检测试卷
一．选择题（共12小题）
1．我国冬奥会将于2022年2月4日在北京，张家口等地召开，并在此之前进行了冬奥会会标征集活动，以下是部分参选作品，其文字上方的图案是中心对称图形的是（　　）

A．①② B．①③ C．② D．②④
2．若式子+有意义，则x满足的条件是（　　）
A．x≠3且x≠﹣3 B．x≠3且x≠4 C．x≠4且x≠﹣5 D．x≠﹣3且x≠﹣5
3．多项式a2﹣9与a2+6a+9的公因式是（　　）
A．a+3 B．a﹣3 C．a+9 D．a﹣9
4．若a＞b，则下列不等式成立的是（　　）
A．﹣9a＞﹣9b B．
C． D．7b﹣c＜7a﹣c
5．在平面直角坐标系中，已知点O（0，0）A（2，4），将线段OA沿x轴向左平移2个单位，再向上平移2个单位，得到O、A两点的对应点分别为O1，A1，则O1，A1的坐标分别是（　　）
A．（﹣2，2），（4，6） B．（﹣2，2），（0，6）
C．（2，﹣2），（4，6） D．（2，﹣2），（0，6）
6．如图，已知▱ABCD中，AE⊥BC于点E，以B为中心，取旋转角等于∠ABC把△BAE顺时针旋转，得到△BA'E'，连接BA'，若∠ADC＝60°，∠ADA'＝50°，则∠DA′E′度数为（　　）

A．130° B．150° C．160° D．170°
7．如图，▱ABCD的对角线AC，BD相交于点O，且AC+BD＝16，若△BCO的周长为14，则AD的长为（　　）

A．12 B．9 C．8 D．6
8．如图，在已知的△ABC中，按以下步骤作图：
①分别以B，C为圆心，以大于BC的长为半径作弧，两弧相交于两点M，N；
②作直线MN交AB于点D，连接CD．
若CD＝AC，∠A＝50°，则∠ACB的度数为（　　）

A．90° B．95° C．100° D．105°
9．如图，△ABC绕点A逆时针旋转40°得到△ADE，∠BAC＝50°，则∠DAC的度数为（　　）

A．10° B．15° C．20° D．25°
10．若分式方程有增根，则m等于（　　）
A．3 B．﹣3 C．2 D．﹣2
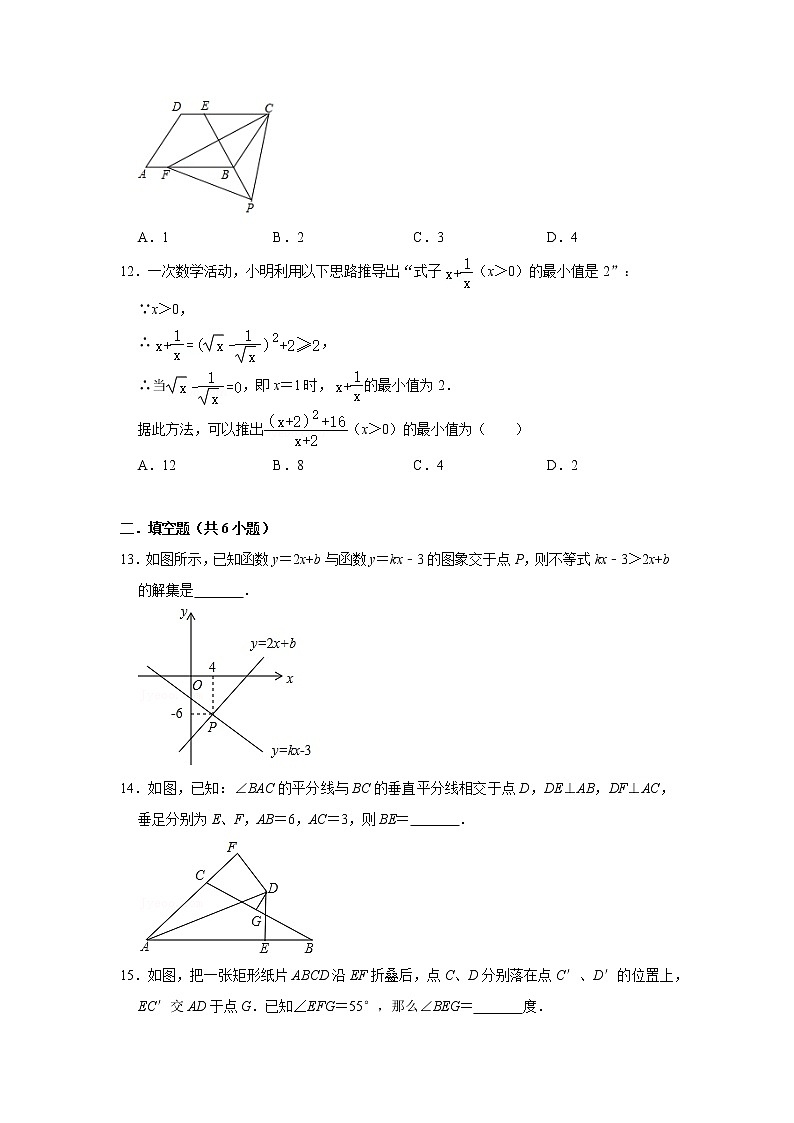
11．如图，四边形ABCD是平行四边形，点E是边CD上一点，且BC＝EC，CF⊥BE交AB于点F，P是EB延长线上一点，下列结论：
①BE平分∠CBF；②CF平分∠DCB；③BC＝FB；④PF＝PC．
其中正确结论的个数为（　　）

A．1 B．2 C．3 D．4
12．一次数学活动，小明利用以下思路推导出“式子（x＞0）的最小值是2”：
∵x＞0，
∴，
∴当，即x＝1时，的最小值为2．
据此方法，可以推出（x＞0）的最小值为（　　）
A．12 B．8 C．4 D．2

二．填空题（共6小题）
13．如图所示，已知函数y＝2x+b与函数y＝kx﹣3的图象交于点P，则不等式kx﹣3＞2x+b的解集是　 　．

14．如图，已知：∠BAC的平分线与BC的垂直平分线相交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F，AB＝6，AC＝3，则BE＝　 　．

15．如图，把一张矩形纸片ABCD沿EF折叠后，点C、D分别落在点C′、D′的位置上，EC′交AD于点G．已知∠EFG＝55°，那么∠BEG＝　 　度．

16．现在有住宿生若干名，分住若干间宿舍，若每间住4人，则还有19人无宿舍住；若每间住6人，则有一间宿舍不空也不满．若设宿舍间数为x，则可以列得不等式组为　 　．
17．如图，AB＝12m，CA⊥AB于A，DB⊥AB于B，且AC＝4m，P点从B向A运动，每分钟走1m，Q点从B向D运动，每分钟走2m，P、Q两点同时出发，运动 　 　分钟后，△CAP与△PQB全等．

18．如图①为Rt△AOB，∠AOB＝90°，其中OA＝3，OB＝4．将AOB沿x轴依次以A，B，O为旋转中心顺时针旋转．分别得图②，图③，…，则旋转到图⑩时直角顶点的坐标是　 　．


三．解答题（共7小题）
19．先化简，然后从﹣1≤x≤2的范围内选取一个你喜欢的整数作为x的值代入求值.

20．解不等式组：，并在数轴上表示出它的解集．

21．如图，D是△ABC边BC的中点，连接AD并延长到点E，使DE＝AD，连接BE．
（1）哪两个图形成中心对称？
（2）已知△ADC的面积为4，求△ABE的面积；
（3）已知AB＝5，AC＝3，求AD的取值范围．

22．数学探究课上老师处这样一道题：“如图，等边△ABC中有一点P，且PA＝3，PB＝4，PC＝5，试求∠APB的度数．”小明和小军探讨时发现了一种求∠APB度数的方法，下面是这种方法的一部分思路，请按照下列思路要求画图或判断
（1）在图中画出△APC绕点A顺时针旋转60°后的△AP1B；
（2）试判断△AP1P的形状，并说明理由；
（3）试判断△BP1P的形状，并说明理由；
（4）由（2）、（3）两问可知：∠APB＝　 　．

23．在平面直角坐标系xOy中，直线l1：y＝3x与直线l2：y＝kx+b交于点A（a，3），点B（2，4）在直线l2上．
（1）求a的值；
（2）求直线l2的解析式；
（3）直接写出关于x的不等式3x＜kx+b的解集．

24．去冬今春，我市部分地区遭受了罕见的旱灾，“旱灾无情人有情”．某单位给某乡中小学捐献一批饮用水和蔬菜共320件，其中饮用水比蔬菜多80件．
（1）求饮用水和蔬菜各有多少件？
（2）现计划租用甲、乙两种货车共8辆，一次性将这批饮用水和蔬菜全部运往该乡中小学．已知每辆甲种货车最多可装饮用水40件和蔬菜10件，每辆乙种货车最多可装饮用水和蔬菜各20件．则运输部门安排甲、乙两种货车时有几种方案？请你帮助设计出来；
（3）在（2）的条件下，如果甲种货车每辆需付运费400元，乙种货车每辆需付运费360元．运输部门应选择哪种方案可使运费最少？最少运费是多少元？




25．已知点E，F分别是平行四边形ABCD的边BC，CD上的点，∠EAF＝60°．
（1）如图1，若AB＝2，AF＝5，点E与点B，点F与点D分别重合，求平行四边形ABCD的面积；
（2）如图2，若AB＝BC，∠B＝∠EAF＝60°，求证：AE＝AF；
（3）如图3，若BE＝CE，CF＝3DF，AB＝4，AF＝6，求AE的长度．














北师大版八年级下册数学 期末考试检测试卷
参考答案
一．选择题（共12小题）
1．解：图形①③④均不能找到这样的一个点，使图形绕某一点旋转180度后和原图形完全重合，所以不是中心对称图形，
图形②能找到这样的一个点，使图形绕某一点旋转180度后和原图形完全重合，所以是中心对称图形，故选：C．
2．解：∵分式有意义，
∴x﹣3≠0，x﹣4≠0，
∴x≠3且x≠4，故选：B．
3．解：a2﹣9＝（a+3）（a﹣3），a2+6a+9＝（a+3）2，
则多项式a2﹣9与a2+6a+9的公因式为（a+3），故选：A．
4．解：A、因为a＞b，所以﹣9a＜﹣9b，故A不符合题意；
B、因为a＞b，所以b﹣12＜a﹣12，故B不符合题意；
C、因为a＞b，所以a＞b，故C不符合题意；
D、因为a＞b，所以7b﹣c＜7a﹣c，故D符合题意，故选：D．
5．解：线段OA沿x轴向左平移2个单位，再向上平移2个单位，只须让原来的横坐标都减2，纵坐标都加2即可，
∴新横坐标分别为0﹣2＝﹣2，2﹣2＝0，
新纵坐标分别为0+2＝2，4+2＝6．，
即新坐标为（﹣2，2），（0，6），故选：B．
6．解：∵四边形ABCD为平行四边形，
∴∠ABC＝∠ADC＝60°，AD∥BC，
∴∠ADA′+∠DA′B＝180°，
∴∠DA′B＝180°﹣50°＝130°，
∵AE⊥BE，
∴∠BAE＝30°，
∵△BAE顺时针旋转，得到△BA′E′，
∴∠BA′E′＝∠BAE＝30°，
∴∠DA′E′＝130°+30°＝160°，故选：C．
7．解：∵四边形ABCD是平行四边形，
∴AO＝CO＝AC，BO＝DO＝BD，
∵AC+BD＝16，
∴BO+CO＝8，
∵△BCO的周长为14，
∴BC＝6＝AD，故选：D．
8．解：∵CD＝AC，∠A＝50°，
∴∠ADC＝∠A＝50°，
根据题意得：MN是BC的垂直平分线，
∴CD＝BD，
∴∠BCD＝∠B，
∴∠B＝∠ADC＝25°，
∴∠ACB＝180°﹣∠A﹣∠B＝105°，故选：D．
9．解：由旋转的性质可知，∠BAD＝40°，
∵∠BAC＝50°，
∴∠DAC＝∠BAC﹣∠BAD＝50°﹣40°＝10°，故选：A．
10．解：分式方程去分母得：x﹣3＝m，
由分式方程有增根，得到x﹣1＝0，即x＝1，
把x＝1代入整式方程得：m＝﹣2，故选：D．
11．证明：∵BC＝EC，
∴∠CEB＝∠CBE，
∵四边形ABCD是平行四边形，
∴DC∥AB，
∴∠CEB＝∠EBF，
∴∠CBE＝∠EBF，
∴①BE平分∠CBF，正确；
∵BC＝EC，CF⊥BE，
∴∠ECF＝∠BCF，
∴②CF平分∠DCB，正确；
∵DC∥AB，
∴∠DCF＝∠CFB，
∵∠ECF＝∠BCF，
∴∠CFB＝∠BCF，
∴BF＝BC，
∴③正确；
∵FB＝BC，CF⊥BE，
∴B点一定在FC的垂直平分线上，即PB垂直平分FC，
∴PF＝PC，故④正确．故选：D．
12．解：∵x＞0，
∴x+2＞0．
∴＝（x+2）+＝（﹣）2+8≥8．
当﹣＝0，即x＝2时，的最小值是8，故选：B．
二．填空题（共6小题）
13．解：∵函数y＝2x+b与函数y＝kx﹣3的图象交于点P（4，﹣6），
∴不等式kx﹣3＞2x+b的解集是x＜4，故答案为x＜4．
14．解：连接CD，BD，

∵AD是∠BAC的平分线，DE⊥AB，DF⊥AC，
∴DF＝DE，∠F＝∠DEB＝90°，∠ADF＝∠ADE，
∴AE＝AF，
∵DG是BC的垂直平分线，
∴CD＝BD，
在Rt△CDF和Rt△BDE中，，∴Rt△CDF≌Rt△BDE（HL），
∴BE＝CF，
∴AB＝AE+BE＝AF+BE＝AC+CF+BE＝AC+2BE，
∵AB＝6，AC＝3，
∴BE＝1.5，故答案为：1.5．
15．解：∵AD∥BC，
∴∠CEF＝∠EFG＝55°，
由折叠的性质，得∠GEF＝∠CEF＝55°，
∴∠BEG＝180°﹣∠GEF﹣∠CEF＝70°，故答案为：70．
16．解：∵若每间住4人，则还有19人无宿舍住，
∴学生总人数为（4x+19）人，
∵一间宿舍不空也不满，
∴学生总人数﹣（x﹣1）间宿舍的人数在1和5之间，
∴列的不等式组为：.
17．解：∵CA⊥AB于A，DB⊥AB于B，
∴∠A＝∠B＝90°，
设运动x分钟后△CAP与△PQB全等，则BP＝xm，BQ＝2xm，则AP＝（12﹣x）m，
分两种情况：①若BP＝AC，则x＝4，
AP＝12﹣4＝8，BQ＝8，AP＝BQ，
∴△CAP≌△PBQ；
②若BP＝AP，则12﹣x＝x，
解得：x＝6，BQ＝12（m）≠AC，
此时△CAP与△PQB不全等；
综上所述：运动4分钟后△CAP与△PQB全等，故答案为：4．
18．解：∵∠AOB＝90°，OA＝3，OB＝4，
∴AB＝＝＝5，
根据图形，每3个图形为一个循环组，3+5+4＝12，
所以，图⑨的直角顶点在x轴上，横坐标为12×3＝36，
所以，图⑨的顶点坐标为（36，0），
又∵图⑩的直角顶点与图⑨的直角顶点重合，
∴图⑩的直角顶点的坐标为（36，0），故答案为：（36，0）．
三．解答题（共7小题）
19．解：原式＝•＝，
∵x≠±1，x≠2，
∴可取x＝0，
则原式＝﹣．
20．解：解不等式①，得：x＜5，
解不等式②，得：x≥﹣2，
则不等式组的解集为﹣2≤x＜5，
将不等式组的解集表示在数轴上如下：

21．解：（1）图中△ADC和三角形EDB成中心对称；
（2）∵△ADC和三角形EDB成中心对称，△ADC的面积为4，
∴△EDB的面积也为4，
∵D为BC的中点，
∴△ABD的面积也为4，所以△ABE的面积为8；
（3）∵在△ABD和△ECD中，，∴△ABD≌△ECD（SAS），
∴AB＝EC，
∵△ACE中，AB﹣AC＜AE＜AC+AB，
∴2＜AE＜8，
∴1＜AD＜4．

22．解：（1）如图，△AP1B为所作；
（2）连接PP1，如图，

△AP1P为等边三角形．理由如下：
∵△APC绕点A顺时针旋转60°后的△AP1B，
∴AP1＝AP，∠PAP1＝60°，
∴△AP1P为等边三角形；
（3）△BP1P为直角三角形．
理由如下：
∵△APC绕点A顺时针旋转60°后的△AP1B，
∴BP1＝PC＝5，
∵△AP1P为等边三角形，
∴PP1＝AP＝3，
∵PP12+PB2＝BP12，
∴△BP1P为直角三角形，∠BPP1＝90°；
（3）∵△AP1P为等边三角形，
∴∠APP1＝60°，
而∠BPP1＝90°；
∴∠AP1B＝90°+60°＝150°，
∵△APC绕点A顺时针旋转60°后的△AP1B，
∴∠BPC＝∠AP1B＝150°，故答案为150°．
23．解：（1）直线 l1：y＝3x 与直线 l2：y＝kx+b 交于点 A（a，3），所以3a＝3．
解得a＝1．
（2）由（1）得点 A（1，3），
直线 l2：y＝kx+b 过点 A（1，3），点 B （ 2，4 ），
所以，解得，所以直线 l2 的解析式为 y＝x+2，
（3）不等式3x＜kx+b的解集为x＜1．

24．解：（1）设饮用水有x件，则蔬菜有（x﹣80）件．
x+（x﹣80）＝320，解得x＝200．
∴x﹣80＝120．
答：饮用水和蔬菜分别为200件和120件；
（2）设租用甲种货车m辆，则租用乙种货车（8﹣m）辆．
由题意得：，解得2≤m≤4．
∵m为正整数，
∴m＝2或3或4，安排甲、乙两种货车时有3种方案．
设计方案分别为：
①甲车2辆，乙车6辆；②甲车3辆，乙车5辆；③甲车4辆，乙车4辆；
（3）3种方案的运费分别为：
①2×400+6×360＝2960（元）；
②3×400+5×360＝3000（元）；
③4×400+4×360＝3040（元）；
∴方案①运费最少，最少运费是2960元．
答：运输部门应选择甲车2辆，乙车6辆，可使运费最少，最少运费是2960元．
25．（1）解：过点B作BH⊥AD于H，如图1所示，

在Rt△ABH中，∠BAD＝60°，
∴∠ABH＝30°，
∵AB＝2，
∴AH＝1，BH＝＝＝，
∴S▱ABCD＝AD×BH＝AF×BH＝5×＝5；
（2）证明：连接AC，如图2所示，

∵AB＝BC，∠B＝∠EAF＝60°，
∴△ABC是等边三角形，
∴AB＝AC，∠BAC＝∠ACB＝60°，
∴∠BAE＝∠CAF，
∵四边形ABCD是平行四边形，AB＝AC，
∴四边形ABCD是菱形，
∴∠ACF＝∠ACB＝60°，
∴∠B＝∠ACF，
在△ABE和△ACF中，，∴△ABE≌△ACF（ASA），
∴AE＝AF；
（3）解：延长AE交DC延长线于P，过点F作FG⊥AP于G，如图3所示，

∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠B＝∠ECP，
在△ABE和△PCE中，，∴△ABE≌△PCE（ASA），
∴AE＝PE，PC＝AB＝CD＝4，
∵CF＝3DF，
∴CF＝3，
∴PF＝7，
在Rt△AFG中，AF＝6，∠EAF＝60°，
∴∠AFG＝30°，
∴AG＝AF＝3，FG＝＝＝3
在Rt△PFG中，由勾股定理得：PG＝＝＝，
∴AP＝AG+PG＝3+，
∴AE＝PE＝AP＝．