2022年山东省济南市中考数学考前模拟冲刺试题

这是一份2022年山东省济南市中考数学考前模拟冲刺试题，共18页。

2022年山东省济南市中考数学考前模拟冲刺试题
（考试时间：120分钟 满分：150分）
第Ⅰ卷（选择题 共48分）
一．选择题（共12小题，满分48分，每小题4分）
1．（4分）下列四个数中，最大的实数是（　　）
A．-23 B．0 C．2 D．23
2．（4分）如图所示放置的几何体，它的俯视图是（　　）

A． B． C． D．
3．（4分）天津国家会展中心建成后将成为中国北方最大的国家级会展中心，它的总建筑面积为1340000m2．将1340000用科学记数法可表示为（　　）
A．0.134×107 B．1.34×106 C．13.4×105 D．134×104
4．（4分）如图，直线AB∥CD，直线EF分别与直线AB、CD相交于点G、H，若∠2＝35°，则∠1的度数为（　　）

A．165° B．155° C．145° D．135°
5．（4分）计算a-1a+1a，正确的结果是（　　）
A．1 B．12 C．a D．1a
6．（4分）有甲、乙两个不透明的袋子，甲袋子里放有四个完全一样的球，标号分别为1、2、3、4；乙袋子里装有三个完全一样的球，标号分别为1、2、3，分别从甲、乙两个袋子里各拿出一个球，两个球标号相同的概率是（　　）
A．56 B．14 C．23 D．12
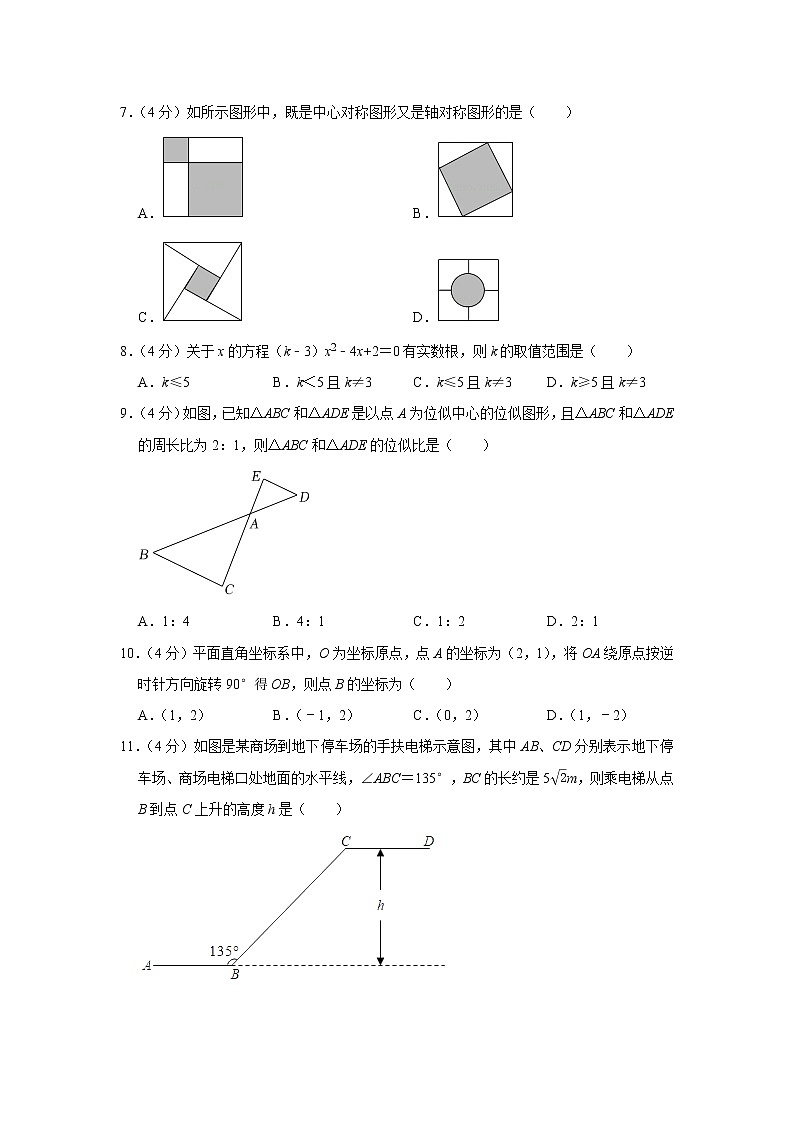
7．（4分）如所示图形中，既是中心对称图形又是轴对称图形的是（　　）
A． B．
C． D．
8．（4分）关于x的方程（k﹣3）x2﹣4x+2＝0有实数根，则k的取值范围是（　　）
A．k≤5 B．k＜5且k≠3 C．k≤5且k≠3 D．k≥5且k≠3
9．（4分）如图，已知△ABC和△ADE是以点A为位似中心的位似图形，且△ABC和△ADE的周长比为2：1，则△ABC和△ADE的位似比是（　　）

A．1：4 B．4：1 C．1：2 D．2：1
10．（4分）平面直角坐标系中，O为坐标原点，点A的坐标为（2，1），将OA绕原点按逆时针方向旋转90°得OB，则点B的坐标为（　　）
A．（1，2） B．（﹣1，2） C．（0，2） D．（1，﹣2）
11．（4分）如图是某商场到地下停车场的手扶电梯示意图，其中AB、CD分别表示地下停车场、商场电梯口处地面的水平线，∠ABC＝135°，BC的长约是52m，则乘电梯从点B到点C上升的高度h是（　　）

A．522m B．5m C．52m D．10m
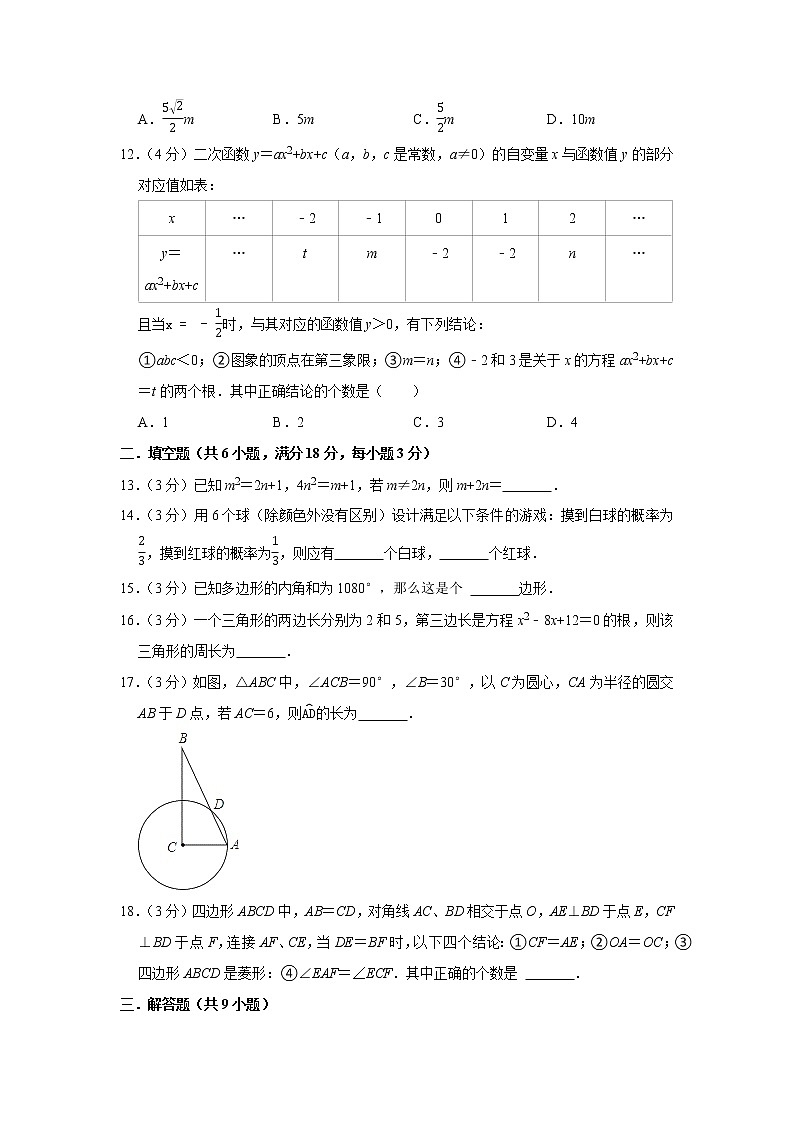
12．（4分）二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）的自变量x与函数值y的部分对应值如表：
x
…
﹣2
﹣1
0
1
2
…
y＝ax2+bx+c
…
t
m
﹣2
﹣2
n
…
且当x=-12时，与其对应的函数值y＞0，有下列结论：
①abc＜0；②图象的顶点在第三象限；③m＝n；④﹣2和3是关于x的方程ax2+bx+c＝t的两个根．其中正确结论的个数是（　　）
A．1 B．2 C．3 D．4
二．填空题（共6小题，满分18分，每小题3分）
13．（3分）已知m2＝2n+1，4n2＝m+1，若m≠2n，则m+2n＝　 　．
14．（3分）用6个球（除颜色外没有区别）设计满足以下条件的游戏：摸到白球的概率为23，摸到红球的概率为13，则应有　 　个白球，　 　个红球．
15．（3分）已知多边形的内角和为1080°，那么这是个 　 　边形．
16．（3分）一个三角形的两边长分别为2和5，第三边长是方程x2﹣8x+12＝0的根，则该三角形的周长为　 　．
17．（3分）如图，△ABC中，∠ACB＝90°，∠B＝30°，以C为圆心，CA为半径的圆交AB于D点，若AC＝6，则AD的长为　 　．

18．（3分）四边形ABCD中，AB＝CD，对角线AC、BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连接AF、CE，当DE＝BF时，以下四个结论：①CF＝AE；②OA＝OC；③四边形ABCD是菱形：④∠EAF＝∠ECF．其中正确的个数是 　 　．
三．解答题（共9小题）
19．(13-2)-1+3-827+(6-2)0．
20．解不等式组：1+2x＞3+x5x＜4x-1．
21．如图，在菱形ABCD中，E、F分别是AB和BC上的点，且AE＝CF．
（1）求证：△ADE≌△CDF；
（2）若∠ADC＝150°，∠CDF＝50°，求∠EDB的度数．

22．2021～2023年是我县国家文明卫生城市的创建周期，它是我县民生工程的一件盛事，我县委托第三方评估机构进行创建评估，以了解10～60岁年龄段市民对本轮创建的关注程度，随机选取了100名年龄在该范围内的市民进行了调查，并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图，如表所示：
组别
年龄段
频数（人数）
第1组
10≤x＜20
5
第2组
20≤x＜30
a
第3组
30≤x＜40
35
第4组
40≤x＜50
20
第5组
50≤x＜60
15
（1）请直接写出a＝　 　，m＝　 　；
（2）第3组人数在扇形统计图中所对应的圆心角是 　 　°；
（3）假设我县现有10～60岁的市民70万人，问40～50岁年龄段的关注本轮创建国家文明卫生城市的人数约有多少？

23．如图，AB是圆O的弦，OA⊥OD，AB，OD相交于点C，且CD＝BD．
（1）判断BD与圆O的位置关系，并证明你的结论；
（2）当OA＝3，OC＝1时，求线段BD的长．

24．Ⅰ号无人机从海拔10m处出发，以10m/min的速度匀速上升，Ⅱ号无人机从海拔30m处同时出发，以a（m/min）的速度匀速上升，经过5min两架无人机位于同一海拔高度b（m）．无人机海拔高度y（m）与时间x（min）的关系如图．两架无人机都上升了15min．
（1）求b的值及Ⅱ号无人机海拔高度y（m）与时间x（min）的关系式；
（2）问无人机上升了多少时间，Ⅰ号无人机比Ⅱ号无人机高28米．

25．已知点P的坐标为（m，0），点Q在x轴上（不与P重合），以PQ为边，∠PQM＝60°作菱形PQMN，使点M落在反比例函数y=-23x的图象上．
（1）如图所示，若点P的坐标为（1，0），求出图中点M的坐标；
（2）当P（1，0）时，在（1）图中已经画出一个符合条件的菱形PQMN，请您在原图上画出另一个符合条件的菱形PQ1M1N1，并求点M1的坐标；
（3）随着m的取值不同，这样的菱形还可以画出三个和四个，当符合上述条件的菱形刚好能画出三个时，请直接写出点M的坐标．

26．如图，在平面直角坐标系中，点A、C分别在x轴、y轴上，四边形ABCO为矩形，BC＝6，点D与点A关于y轴对称，sin∠ACB=45．点E、F分别是线段AD、AC上的动点（点E不与A、D点重合），且∠CEF＝∠ACB．
（1）求AC的长与点D的坐标．
（2）说明△AEF与△DCE相似．
（3）当△EFC为等腰三角形时，求点E的坐标．

27．如图：已知抛物线y＝x2+px+q与x轴交于A，B两点（A点在B点的左边），交y轴负半轴于C点．
（1）若p＝﹣2，q＝﹣3，请求出抛物线的顶点坐标．
（2）若∠ACB＝90°，且1OA-1OB=2OC
①求△ABC的外接圆的半径
②能否在x轴上找有一点E，抛物线上找到一点F，使以A，C，E，F为顶点的四边形为平行四边形？若有，请直接写出符合条件所有E，F点的坐标．（此小问不要求写解答过程）


参考答案与试题解析
一．选择题（共12小题，满分48分，每小题4分）
1．【解答】解：∵-23＜0＜23＜2，
∴四个数中，最大的实数是2．
故选：C．
2．【解答】解：从上面看，是两个同心圆．
故选：B．
3．【解答】解：1340000＝1.34×106．
故选：B．
4．【解答】解：∵AB∥CD，∠2＝35°，
∴∠1+∠2＝180°，
∴∠1＝180°﹣∠2＝145°．
故选：C．
5．【解答】解：原式=a-1+1a=1．
故选：A．
6．【解答】解：画树状图如图：

共有12个等可能的结果，其中两个球标号相同的结果有3个，
∴两个球标号相同的概率为312=14，
故选：B．
7．【解答】解：A．是轴对称图形，不是中心对称图形，故本选项不符合题意；
B．不是轴对称图形，是中心对称图形，故本选项不符合题意；
C．不是轴对称图形，是中心对称图形，故本选项不符合题意；
D．既是轴对称图形，又是中心对称图形，故本选项符合题意；
故选：D．
8．【解答】解：当k﹣3＝0，即k＝3，方程化为﹣4x＝2，解得x=-12；
当k﹣3≠0时，Δ＝（﹣4）2﹣4（k﹣3）×2≥0，解得k≤5且k≠3，
综上所述，k的范围为k≤5．
故选：A．
9．【解答】解：∵△ABC和△ADE是以点A为位似中心的位似图形，
∴△ABC∽△ADE，位似比等于相似比，
∵△ABC和△ADE的周长比为2：1，
∴△ABC和△ADE的相似比为2：1，
∴△ABC和△ADE的位似比是2：1．
故选：D．
10．【解答】解：如图，B（﹣1，2）

故选：B．
11．【解答】解：如图，作CH⊥AB于H．

在Rt△CBH中，∵∠CHB＝90°，BC＝52m，∠CBH＝45°，
∴sin45°=CHBC，
∴CH＝BC×22=5（m）．
故选：B．
12．【解答】解：∵抛物线经过（0，﹣2），（1，﹣2），
∴c＝﹣2，抛物线对称轴为直线x=-b2a=12，
∴b＝﹣a，即ab＜0，
∴abc＞0，①错误．
∵抛物线对称轴为直线x=12＞0，
∴②错误．
∵2-12=12-（﹣1），
∴（﹣1，m），（2，n）关于对称轴对称，
∴m＝n，③正确．
∵抛物线经过（﹣2，t），抛物线对称轴为直线x=12，
∴抛物线经过（3，t），即﹣2和3是关于x的方程ax2+bx+c＝t的两个根，④正确．
故选：B．
二．填空题（共6小题，满分18分，每小题3分）
13．【解答】解：∵m2＝2n+1，4n2＝m+1，
∴m2﹣4n2＝2n+1﹣m﹣1，
∴m2﹣4n2＝2n﹣m，
∴（m+2n）（m﹣2n）＝2n﹣m，
∵m≠2n，
∴m+2n＝﹣1．
故答案为﹣1．
14．【解答】解：根据概率公式P（A）=mn，m＝n×P（A），
则有6×23=4个白球，6×13=2个红球．
故答案为：4，2．
15．【解答】解：由题意可得：
（n﹣2）×180°＝1080°，
解得n＝8，
故答案为：八．
16．【解答】解：∵x2﹣8x+12＝0，
∴（x﹣2）（x﹣6）＝0，
∴x1＝2，x2＝6，
∵三角形的两边长分别为2和5，第三边长是方程x2﹣8x+12＝0的根，2+2＜5，2+5＞6，
∴三角形的第三边长是6，
∴该三角形的周长为：2+5+6＝13．
故答案为：13．
17．【解答】解：如图，连接CD，
∵∠ACB＝90°，∠B＝30°，AC＝6
∴AB＝2AC＝12
∵CD＝AC＝6，∠A＝90°﹣30°＝60°
∴∠ACD＝60°
∴AD的长为：60π⋅6180=2π．

18．【解答】解：如图，∵DE＝BF，
∴DE﹣EF＝BF﹣EF，
即BE＝DF，
∵AE⊥BD于点E，CF⊥BD于点F，
∴∠AEB＝∠CFD＝90°，
在Rt△ABE和Rt△CDF中，
AB=CDBE=DF，
∴Rt△ABE≌Rt△CDF（HL），
∴AE＝CF，故①正确；
∵AE⊥BD于点E，CF⊥BD于点F，
∴AE∥FC，
∵AE＝CF，
∴四边形CFAE是平行四边形，
∴OA＝OC，∠EAF＝∠ECF，故②、④正确，
∵Rt△ABE≌Rt△CDF，
∴∠ADE＝∠CBF，
∴AB∥CD，
∵AB＝CD，
∴四边形ABCD是平行四边形，
没有条件证出四边形ABCD是菱形，故③错误；
故答案为：①②④．

三．解答题（共9小题）
19．【解答】解：(13-2)-1+3-827+(6-2)0
=3-2+（-23）+1
=3-53．
20．【解答】解：1+2x＞3+x①5x＜4x-1②，
解①得x＞2，
解②得x＜﹣1，
所以不等式组无解．
21．【解答】解：（1）∵四边形ABCD是菱形，
∴∠A＝∠C，AB＝CB，AD＝DC，
在△ADE和△CDF中，
AD=DC∠A=∠CAE=CF，
∴△ADE≌△CDF（SAS）；

（2）∵△ADE≌△CDF，
∴∠ADE＝∠CDF，
∵四边形ABCD是菱形，∠ADC＝150°，
∵∠ADB=12∠ADC＝75°，
∵∠CDF＝50°，
∴∠EDB＝∠ADB﹣∠ADE＝∠ADB﹣∠CDF＝25°．
22．【解答】解：（1）a＝100﹣（5+35+20+15）＝25，m%=20100×100%＝20%，即m＝20，
故答案为：25、20；
（2）第3组人数在扇形统计图中所对应的圆心角是360°×35100=126°，
故答案为：126；
（3）40～50岁年龄段的关注本轮创建国家文明卫生城市的人数约有70×20100=14（万人）．
23．【解答】（1）证明：连接OB，
∵OA＝OB，DC＝DB，
∴∠A＝∠ABO，∠DCB＝∠DBC，
∵AO⊥OD，
∴∠AOC＝90°，即∠A+∠ACO＝90°，
∵∠ACO＝∠DCB＝∠DBC，
∴∠ABO+∠DBC＝90°，即OB⊥BD，
则BD为圆O的切线；

（2）解：设BD＝x，则OD＝x+1，而OB＝OA＝3，
在RT△OBD中，OB2+BD2＝OD2，
即32+x2＝（x+1）2，
解得x＝4，
∴线段BD的长是4．

24．【解答】解：（1）b＝10+10×5＝60，
设函数的表达式为y＝kx+t，
将（0，30）、（5，60）代入上式得t=3060=5k+t，解得k=6t=30，
故函数表达式为y＝6x+30（0≤x≤15）；

（2）由题意得：（10x+10）﹣（6x+30）＝28，
解得x＝12＜15，
故无人机上升12min，Ⅰ号无人机比Ⅱ号无人机高28米．
25．【解答】解：（1）如图，过点M作MT⊥PQ于T，设M（a，-23a）．

∵QP＝QM，∠PQM＝60°，
∴△PQM是等边三角形，
∴MT=23a．，PT＝a﹣1，
∵tan60°=MTPT，
∴a-123a=3，
∴a＝2，
∴M（2，-3）．

（2）如下图中，

∵四边形PQ1M1N1是菱形，
∴Q1P＝Q1M1，
∵∠PQ1M1＝60°，
∴△PQ1M1是等边三角形，
∴∠Q1PM1＝60°，
∴直线PM1的解析式为y=-3x+3，
由y=-23xy=-3x+3解得x=-1y=23或x=2y=-3，
∴M1（﹣1，23）．

（3）如下图，当过点P与x轴的夹角为60°的直线与反比例函数的交点的个数只有3个时，满足条件的菱形只有3个．

设直线PM1的解析式为y=3x+b，
由y=-23xy=3x+b，消去y得到：3x2+bx+23=0，
由题意：Δ＝0，
∴b＝±26，
当b＝﹣26时，可得y=3x﹣26，
由：y=-23xy=3x-26，解得x=2y=-6，
∴M1（2，-6），
由y=-23xy=-3x+26解得x=2+2y=6-23或x=2-2y=6+23，
∴M2（2+2，6-23），M2（2-2，6+23），
当b＝26时，同法可得满足条件的点M的坐标为（-2，6）或（-2-2，23-6）或（-2+2，﹣23-6）．
26．【解答】解：（1）由题意sin∠ACB=45，
∴cos∠ACB=35，
∵四边形ABCO为矩形，BC＝6，
∴AC=BCcos∠ACB=10，
∴A点坐标为（﹣6，0），
∵点D与点A关于y轴对称，
∴D（6，0）；
（2）∵点D与点A关于y轴对称，
∴∠CDE＝∠CAO，
∵∠CEF＝∠ACB，∠ACB＝∠CAO，
∴∠CDE＝∠CEF，
∵∠AEC＝∠AEF+∠CEF＝∠CDE+∠DCE，
∴∠AEF＝∠DCE，又∠CDE＝∠CAO，
∴△AEF∽△DCE；
（3）当△EFC为等腰三角形时，有以下三种情况：
①当CE＝EF时，
∵△AEF∽△DCE，
∴△AEF≌△DCE，
∴AE＝CD＝10，
∴OE＝AE﹣OA＝10﹣6＝4，
∴E（4，0）；
②当EF＝FC时，如图所示，过点F作FM⊥CE于M，则点M为CE中点，
∴CE＝2ME＝2EF•cos∠CEF＝2EF•cos∠ACB=65EF．
∵△AEF∽△DCE，
∴EFCE=AECD，即EF65EF=AE10，
解得，AE=253，
∴OE＝AE﹣OA=253-6=73，
∴E（73，0）；
③当CE＝CF时，则∠CFE＝∠CEF，
∵∠CEF＝∠ACB＝∠CAO，
∴∠CFE＝∠CAO，即此时E点与D点重合，这与已知条件矛盾
综上所述，当△EFC为等腰三角形时，点E的坐标为（4，0）或（73，0）．

27．【解答】解：（1）将p、q的值代入抛物线表达式得：y＝x2﹣2x﹣3，
则函数的对称轴为x＝1，
当x＝1时，y＝x2﹣2x﹣3＝﹣4，
故抛物线顶点的坐标为（1，﹣4）；

（2）①设A点横坐标为x1、B点横坐标x2；
∵∠ACO+∠BCO＝90°，∠BCO+∠OBC＝90°，
∴∠ACO＝∠OBC，
∴tan∠ACO＝tan∠OBC，即AOCO=OCOB，
∴﹣x1•x2＝q2①，
令y＝x2+px+q＝0，则x1•x2＝q，x1+x2＝﹣p，
∵且1OA-1OB=2OC
∴x1+x2x1x2=2q②，
将x1•x2＝q代入①式得，﹣q＝q2，
解得q＝﹣1或q＝0（不合题意，舍去）．
将x1•x2＝q，x1+x2＝﹣p代入②式得，-pq=2q，
解得：p＝﹣2，
∴抛物线的解析式y＝x2﹣2x﹣1．
令y＝x2﹣2x﹣1＝0，解得x＝1±2，
即点A、B的坐标分别为（1-2，0）、（1+2，0），
故AB＝1+2-（1-2）＝22，
∵△ABC为直角三角形，故该三角形外接圆的圆心在AB的中点，
则外接圆的半径=12AB=2；
②对于y＝x2﹣2x﹣1，令x＝0，则y＝﹣1，故点C（0，﹣1），
设点E、F的坐标分别为（x，0）、（m，m2﹣2m﹣1），
当AC是边时，
则点A向右平移（2-1）个单位向下平移1个单位得到点C，
同样，点E（F）向右平移（2-1）个单位向下平移1个单位得到点F（E），
∴x+2-1=m0-1=m2-2m-1或x-2+1=m0+1=m2-2m-1，
解得x=3-2m=2或x=2±3m=1±3（不合题意的值已舍去），
故点E、F的坐标分别为（3-2，0）、（2，﹣1）或（2+3，0）、（3+1，1）或（2-3，0）、（1-3，1）；
当AC是对角线时，
由中点公式得：12(1-2+0)=12(x+m)12(0-1)=12(m2-2m-1)，解得m=2x=-2-1（不合题意的值已舍去），
故点E、F的坐标分别为（-2-1，0）、（2，﹣1）；
综上，点E、F的坐标分别为（3-2，0）、（2，﹣1）或（2+3，0）、（3+1，1）或（2-3，0）、（1-3，1）或（-2-1，0）、（2，﹣1）．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/5/25 23:17:27；用户：张航；邮箱：orFmNt2M9nu7kHt3DvbpiZu-gtDQ@weixin.jyeoo.com；学号：28300569