2021-2022学年江苏省盐城中学高二下学期期中数学试题含解析

这是一份2021-2022学年江苏省盐城中学高二下学期期中数学试题含解析，共19页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
2021-2022学年江苏省盐城中学高二下学期期中数学试题
一、单选题
1．已知向量，，若与互相垂直，则的值为（       ）
A．－1 B．2 C． D．1
【答案】B
【分析】根据与互相垂直，可得，再根据数量积的坐标运算即可得解.
【详解】解：因为与互相垂直，
所以，
即，解得.
故选：B.
2．函数的单调递减区间是（       ）
A． B．
C． D．
【答案】D
【分析】的定义域为，利用导函数求解即可.
【详解】由题，的定义域为，且，
令，则或（舍去），
所以当时，；当时，，
所以的单调减区间为，
故选：D
3．为支援上海抗击新冠疫情，盐城市某医院欲从5名医生和3名护士中抽选3人(医生和护士均至少有一人)分配到A，B，C三个地区参加医疗救援(每个地区一人)，由于A地区医生充足，故A地区不再分配医生，则分配方案共有（       ）
A．120种 B．200种 C．216种 D．224种
【答案】A
【分析】先分一名护士去地区，然后再分选择一名医生与一名护士和选择名医生两种情况讨论，从而可得出答案.
【详解】解：由题可知，地区需分得1名护士，有种方法，
此时分两种情况，再选择一名医生和一名护士，有方法，
再选择名医生，有种方法，
故一共有种方法.
故选：A.
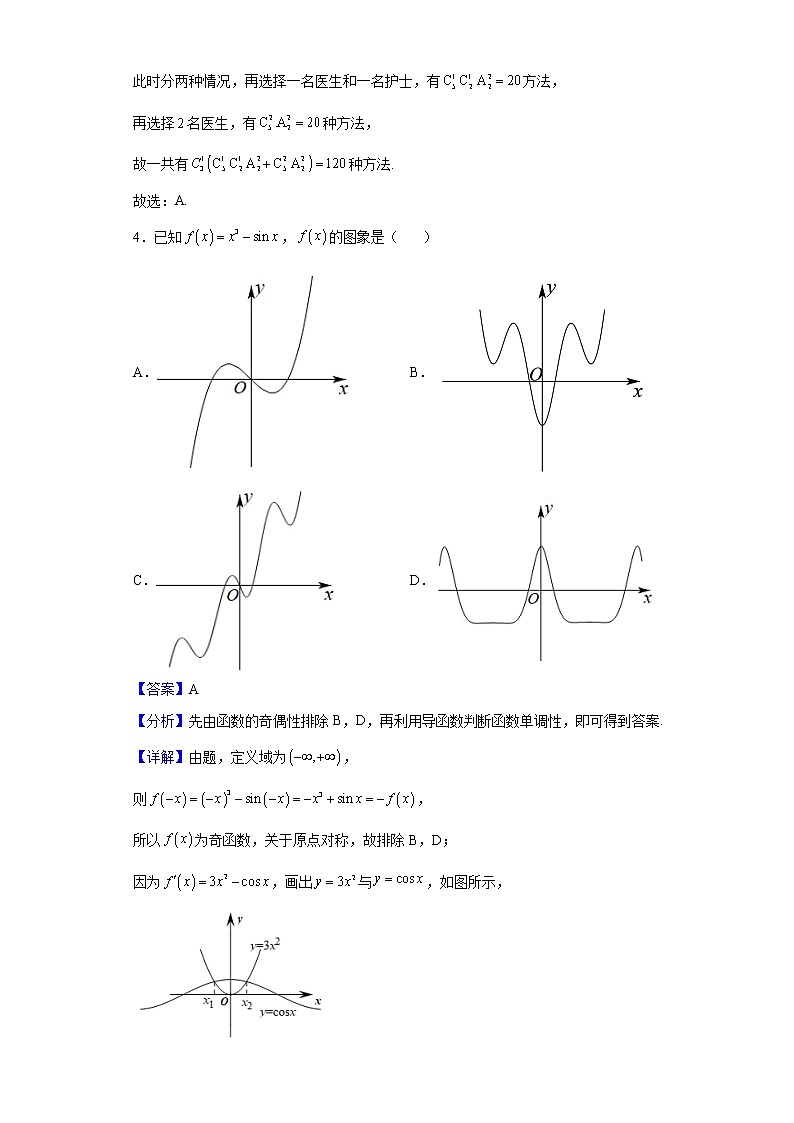
4．已知，的图象是（       ）
A． B．
C． D．
【答案】A
【分析】先由函数的奇偶性排除B，D，再利用导函数判断函数单调性，即可得到答案.
【详解】由题，定义域为，
则，
所以为奇函数，关于原点对称，故排除B，D；
因为，画出与，如图所示，

交于两点，所以当，时，；当时，，
所以当，时，单调递增；当时，单调递减，
故排除C，
故选：A
5．一袋中装有除颜色外完全相同的6个白球和4个黑球，如果不放回地依次摸取3个小球，则在前2次摸到白球的条件下，第3次还摸到白球的概率为（       ）
A． B． C． D．
【答案】C
【分析】设“前2次摸到白球”，“第3次摸到白球”，分别得到和，根据条件概率公式求解即可.
【详解】在这3次摸球过程中，设“前2次摸到白球”，“第3次摸到白球”，
则，
，
所以，
故选：C
6．“杂交水稻之父”袁隆平一生致力于杂交水稻技术的研究，为我国粮食安全、农业科学发展和世界粮食供给作出了杰出贡献．某杂交水稻种植研究所调查某地水稻的株高，得出株高ζ(单位：cm)近似服从正态分布N(80，102)．已知X~N(μ，σ2)时，有P(|x－μ|≤σ)≈0.6827，P(|X－μ|≤2σ)≈0.9545，P(|X－μ|≤3σ)≈0.9973．下列说法错误的是（       ）
A．该地水稻的平均株高约为80cm B．该地水稻株高的方差约为100
C．该地株高低于110cm的水稻约占99.87% D．该地株高超过90cm的水稻约占34.14%
【答案】D
【分析】根据已知条件，结合正态分布的对称性，即可求解．
【详解】解：根据正态分布的定义，
故均值为，方差为，故AB正确；
该地株高低于110cm的水稻所占概率，即该地株高低于110cm的水稻约占99.87%，故C正确；
该地株高超过90cm的水稻所占概率，
即该地株高超过90cm的水稻约占，故D错误.
故选：D.
7．在常压下，六氟化硫是一种无色、无毒、不燃的稳定气体，有良好的绝缘性，在电器工业方面具有广泛用途．六氟化硫分子结构为正八面体结构，如图所示．若此正八面体的内切球的半径为2，则它的棱长为（       ）

A． B．3 C． D．
【答案】C
【分析】设棱长为，利用等体积法求解即可.
【详解】设棱长为，则，
解得，
故选：C
8．若，e为自然对数的底数，则下列结论正确的是（       ）
A． B．
C． D．
【答案】B
【分析】利用导函数来判断函数单调性：利用函数在上的单调性可判断A选项的正误；利用函数在上的单调性可判断B选项的正误；利用函数在上的单调性可判断CD选项的正误.
【详解】对于A选项，构造函数，则，
当时，；当时，，
所以，函数在上单调递增，在上单调递减，
因为函数在上不单调，无法比较、的大小，故A错；
对于B选项，构造函数，则，
当时，，所以在上单调递增，
因为，所以，即，则，故B对；
对于CD选项，构造函数，其中，，
因为函数、在上均为增函数，故函数在上为增函数，
因为，，
所以，存在，使得，
当时，，此时函数单调递减，
当时，，此时函数单调递增，
所以，函数在上不单调，无法比较、的大小，C错，D错.
故选：B
二、多选题
9．下列说法正确的有（       ）
A．设随机变量X服从二项分布B(n，p)，若E(X)＝50，D(X)＝20，则
B．设随机变量ξ服从正态分布N(0，1)，若，则
C．若样本数据的方差为3，则数据的方差为12
D．若从这10件产品(7件正品，3件次品)中任取2件，则恰好取到1件次品的概率
【答案】BC
【分析】选项A. 由二项分布的期望和方差公式可求出，从而判断；选项B.   由正态分布曲线的对称性可判断；选项C. 由方差的性质可判断；选项D. 由古典概率可求解判断.
【详解】选项A. 由随机变量X服从二项分布B(n，p)，则
解得，故选项A不正确.
选项B.   由随机变量ξ服从正态分布N(0，1)，则
所以，故选项B正确.
选项C.   样本数据的方差为3
则数据的方差为，故选项C正确.
选项D.   恰好取到1件次品的概率为 ，故选项D不正确.
故选： BC
10．下列结论中正确的有（       ）
A．＋＝
B．(2x－3)9＝a0＋a1(x－1)＋…＋a9(x－1)9，则a1＋a2＋…＋a9＝2
C．320－1不能被100整除
D．＋＋＋＋＝29
【答案】ABD
【分析】根据组合数的性质即可判断A；分别令和，即可判断B；根据，结合二项式定理即可判断C；根据二项式定理的性质即可判断D.
【详解】解：对于A，由组合数的性质可得＋＝，故A正确；
对于B，令，则，
令，则，
所以，故B正确；
对于C，

，
显然每一项都是的整数倍，
所以320－1能被100整除，故C错误；
对于D，＋＋＋＋表示指数为10的二项式中偶数项的二项式系数之和，
则＋＋＋＋＝29，故D正确.
故选：ABD.
11．如图，在四棱锥E－ABCD中，底面ABCD是边长为4的正方形，△CDE是正三角形，M为线段DE的中点，点N为底面ABCD内的动点，则下列结论正确的是（       ）

A．若BC⊥DE，则平面CDE⊥平面ABCD
B．若BC⊥DE，则直线EA与平面ABCD所成的角的正弦值：
C．若平面CDE⊥平面ABCD，且点N为底面ABCD的中心，则BM＝EN
D．若平面CDE⊥平面ABCD，则四棱锥E－ABCD的体积
【答案】ABD
【分析】对于A，利用线面垂直和面面垂直的判定定理即可判断；对于B，取的中点，连接，利用面面垂直的性质可得平面ABCD，则即为直线EA与平面ABCD所成角的平面角，从而可判断；对于C，分别求出，即可判断；对于D，根据棱锥的体积公式计算即可判断.
【详解】解：对于A，因为BC⊥DE，，
所以直线平面CDE，
又因平面ABCD，
所以平面CDE⊥平面ABCD，故A正确；
对于B，取的中点，连接，
因为△CDE是正三角形，所以，
又平面CDE⊥平面ABCD，平面CDE平面ABCD，平面CDE，
所以平面ABCD，
所以即为直线EA与平面ABCD所成角的平面角，
再中，，
则，
即直线EA与平面ABCD所成的角的正弦值为，故B正确；
对于C，若平面CDE⊥平面ABCD，
则，
因为平面CDE平面ABCD，，平面ABCD，
所以平面CDE，
又平面CDE，所以，
则，
所以，故C错误；
对于D，若平面CDE⊥平面ABCD，
由B得，平面ABCD，
则，故D正确.
故选：ABD.

12．定义在上的函数，满足，则下列说法正确的有（       ）
A．对任意恒成立
B．时，的图象位于x轴下方
C．有且只有两个极值点
D．若恒成立，则
【答案】AB
【分析】A：，利用导函数判断单调性，即可判断选项A；B：由时，的正负即可判断；C：利用导函数判断即可；D：整理不等式为，设，转化问题为求的最小值，即可判断.
【详解】A：因为，即，
设，则，
所以在，，所以，故正确；
B：由题，当时，，，所以，故正确；
C：设，则，
令，则，如图所示，

与只有一个交点，
设交点横坐标为，因为当时，，所以，则，时，；时，，故有且只有一个极值点，故错误；
D：恒成立，则恒成立，
设，则，
令，则，因为，
所以当时，；，，
所以，
所以，故错误.
故选：AB
三、填空题
13．若拋掷4枚质地、大小完全一样的硬币，则正面向上的硬币枚数为1或者4的概率为________．
【答案】0.3125
【分析】根据二项分布的概率公式即可求解
【详解】设表示4枚硬币中正面朝上的硬币数量，则，
则，，
则，
故答案为：
14．某市一水电站的年发电量y(单位：亿千瓦时)与该市的年降雨量x(单位：毫米)有如下统计数据：

2017年
2018年
2019年
2020年
2021年
降雨量x（hm）
1500
1400
1900
1600
2100
发电量y（亿千瓦时）
7.4
7.0
9.2
7.9
10.0
若由表中数据求得线性回归方程为y＝0.004x＋a，由气象部门预估2022年的降雨量约为2000毫米，请你预测2022年发电量约为__________亿千瓦时．
【答案】
【分析】根据样本中心点求得，进而求得预测值.
【详解】解：，
，
所以，
所以，
当，亿千瓦时.
故答案为：
15．数学中有一类顺读与倒读都是同一个数的自然数，称为“回文数”，如22，585，3443等．由数字0，1，2，3，4，5，6可以组成5位“回文数”的个数为_________．
【答案】294
【分析】依据回文数对称的特征，可知万位和个位数字相同，千位和十位数字相同，且万位数字不为0，进而求解.
【详解】依据回文数对称的特征，
万位和个位数字相同，千位和十位数字相同，
万位数字，从1，2，3，4，5，6中取一个，有6种选择；
千位数字，从0，1，2，3，4，5，6中取一个，有7中选择；
百位数字，从0，1，2，3，4，5，6中取一个，有7中选择，
则有，
故答案为：294
16．当a＞0时，若不等式恒成立，则的最小值是__________．
【答案】
【分析】先将不等式转化为，进而转化为的图像恒在图像的下方，求出两个函数的零点，比较两个函数的零点得到，
且当恰为在处的切线时取得最小值，即可求解.
【详解】由题意知：，由可得，即不等式恒成立，令，
易得为斜率大于0的一条直线，；，当时，单增，
当时，单减，又，要使不等式恒成立，必有的零点与的零点重合
或者在的零点左侧，如图所示：

故有，解得，当且仅当恰为在处的切线时取等，此时的图像恒在图像的下方，
即满足恒成立，即恒成立.又，故在处的切线方程为，
即时，取得最小值.
故答案为：.
四、解答题
17．（1）把6本不同的书分给3位学生，每人2本，共有多少种不同的分法?
（2）学校组建了“数学建模社”和“数学文化社”，高二(8)班某小组共有9人参加，其中3人只参加“数学建模社”，4人只参加“数学文化社”，还有2人两个社团都参加了.现从中选出5人参加数学展示活动，其中2人展示“数学建模”，3人展示“数学文化”，共有多少种不同的选法?
【答案】（1）90；（2）124.
【分析】（1）先分组，后分配；
（2）将被选取的多面手（参加两个社团的人）分类讨论.
【详解】(1)       先将6本书平均分成3组，共，再分配给三个学生
所以共有90种不同的分法；
(2)       ①无多面手（参加两个社团的人）参与展示数学建模：；
     ②1个多面手参与展示数学建模：；
     ③2个多面手参与展示数学建模：.
   所以共有60+60+4=124种选法.
18．已知的展开式中前三项的二项式系数之和为22．
(1)求展开式中的常数项；
(2)求展开式中系数最大的项．
【答案】(1)135
(2)
【分析】（1）根据前三项二项式系数和求得，利用通项公式求解展开式中的常数项即可.（2）不妨设第项系数最大，利用最大项的系数不小于相邻两项的系数列式求出的取值范围，由为整数确定出的值，进而求出最大项.
【详解】(1)由题意，展开式前三项的二项式系数和为22.
前三项二项式系数和为：，
解得：或(舍去)，即的值为6，
由通项公式，
令,可得：，
所以展开式中的常数项为
(2)设第项系数最大，则
解之得
因为，所以，
所以展开式中系数最大的项为
19．如图，在三棱台ABC－中，＝B1C1＝C1C=2，AB⊥BC，平面AA1B1B⊥平面BB1C1C．

(1)证明：AB⊥平面BB1C1C；
(2)若AB＝2，则求二面角B－C1C－A的大小．
【答案】(1)见解析
(2)
【分析】（1）在等腰梯形中，作，利用勾股定理得到，再利用面面垂直的性质定理得到，即可得证.
（2）建立空间直角坐标系，写出相应点的坐标，求出平面与平面的法向量，由二面角的向量公式代入即可得出答案.
【详解】(1)
在等腰梯形中，作，，则，在中，，中，，解得，
，即
由平面平面，平面平面，
平面     
，平面
平面.
(2)如图，在平面内，过点作，以为原点，以所在的直线为轴建立空间直角坐标系，

设，则

设平面的法向量为，
则，即，则
平面的一个法向量为
则，所以结合图可知，二面角B－C1C－A的大小为.
20．高校Q为吸引更多优秀的大学本科生加入该校的研究生院进一步深造，在全国硕士研究生统考前，单独组织夏令营考试．考试分为两轮，第一轮为笔试，需要考2门学科，每科笔试成绩从高到低依次有A＋ABC四个等级．若两科笔试成绩均为A＋，则直接被该校提前录取；若一科笔试成绩为A＋，另一科笔试成绩不低于B，则要参加第二轮面试，面试通过也将被该校提前录取，否则均不能被该校提前录取．现甲、乙两人报名参加，两人互不影响．甲在每科笔试中取得A＋ABC的概率分别为，，，；乙在每科笔试中取得A＋ABC的概率分别为，，，，甲、乙在面试中通过的概率分别为，．
(1)求甲需要参加第二轮面试的概率P1；
(2)求甲、乙都被高校Q提前录取的概率P2．
【答案】(1)
(2)
【分析】（1）甲需要参加第二轮面试即笔试的成绩为一科笔试成绩为A＋，另一科笔试成绩不低于B，进而求解即可.
（2）被高校Q提前录取的情况有两种，分别求得甲、乙被高校Q提前录取的概率，进而得到答案.
【详解】(1)由题，甲需要参加第二轮面试，需满足笔试的成绩为一科笔试成绩为A＋，另一科笔试成绩不低于B（且不为A＋，即为A或B）

(2)甲被提前录取的概率为：，
乙被提前录取的概率为：，
所以甲、乙都被高校Q提前录取的概率为
21．火龙果的甜度一般在11－20度之间，现对某火龙果种植基地在新、旧施肥方法下种植的火龙果的甜度作对比，从新、旧施肥方法下种植的火龙果中各随机抽取了200个火龙果，根据水果甜度(单位：度)进行分组，若按[11，12)，[12，13)，[13，14)，[14，15)，[15，16)，[16，17)，[17，18)，[18，19)，[19，20]分组，旧施肥方法下的火龙果的甜度的频率分布直方图与新施肥方法下的火龙果的甜度的频数分布表如下所示．若规定甜度不低于15度为“超甜果”，其他为“非超甜果”．
甜度









频数
10
16
24
20
32
28
36
24
10
新施肥方法下的火龙果的甜度的频数分布表

(1)设两施肥方法下的火龙果的甜度相互独立，记A表示事件：“旧施肥方法下的火龙果的甜度不低于15度，新施肥方法下的火龙果的甜度低于15度”，以样本估计总体，求事件A的概率．
(2)根据上述样本数据，列出2×2列联表，并判断是否有99.5%的把握认为是否为“超甜果”与施肥方法有关?
(3)以样本估计总体，若从旧施肥方法下的200个火龙果中按“超甜果”与“非超甜果”的标准划分，采用分层抽样的方法抽取5个，再从这5个火龙果中随机抽取3个，设“非超甜果”的个数为ξ，求随机变量ξ的分布列及数学期望．
附：，其中n＝a＋b＋c＋d．
P(K2≥k0)
0.025
0.01
0.005
k0
5.024
6.635
7.879
【答案】(1)
(2)列联表见解析，有99.5%的把握认为是否为“超甜果”与施肥方法有关．
(3)分布列见解析，
【分析】（1）首先根据频率分布表，计算新方法下的火龙果的甜度低于15度的频率、旧方法下的火龙果的甜度不低于15度的频率，再利用独立事件概率求；
（2）由题意可得列联表，求计算，再根据临界值，即可判断；
（3）由题意可得随机变量的所有可能取值为1，2，3，再利用超几何概率分布，求分布列和数学期望.
【详解】(1)记表示事件：“旧施肥方法下的火龙果的甜度不低于15度”，表示事件：“新施肥方法下的火龙果的甜度低于15度”，
则有．
由频率分布直方图可知旧施肥方法下的火龙果的甜度不低于15度的频率为．
由频数分布表可知新施肥方法下的火龙果的甜度低于15度的频率为．
故事件的概率为．
(2)依题意可得到列联表

非超甜果
超甜果
合计
旧施肥方法
120
80
200
新施肥方法
70
130
200
合计
190
210
400
，
故有99.5%的把握认为是否为“超甜果”与施肥方法有关．
(3)旧施肥方法下的200个火龙果中，“非超甜果”为120个，“超甜果”为80个，按分层抽样的方法随机抽取5个，则抽取的“非超甜果”为3个，“超甜果”为2个，所以随机变量的所有可能取值为1，2，3.
，，，
随机变量的分布列为

1
2
3




数学期望．
22．已知，函数，其中．
(1)函数满足，当时，的单调区间；
(2)是否存在实数的值，使得对任意的，都有恒成立，若存在，则求出的值；若不存在，则请说明理由；
(3)证明：有唯一极值点，且．
【答案】(1)单调减区间：，单调增区间：
(2)不存在，理由见解析
(3)证明见解析
【分析】（1）当时，，由于，则可根据的正负进而得到的单调区间；
（2）转化问题为的解集为，进而求解即可；
（3）整理，可判断其导函数为单调增函数，由（2）可得，，则在上有唯一零点，即有唯一极值点，再根据整理可得，通过分析法证明即可.
【详解】(1)由题，当时，，
因为，令，则，
所以当时，，当时，，
所以在上单调递减，在上单调递增.
(2)不存在，理由如下：
对任意的，都有恒成立，即的解集为，
则或的解集为，所以，即，
设，则，当时，，
所以，所以方程无解，
故不存在实数，使得对任意的，都有恒成立.
(3)证明：，，
则，
所以在上是增函数，
由（2）可得，，，
所以在上有唯一零点，即在上有唯一零点，
当时，，单调递减；当时，，单调递增，
所以有唯一极小值点，且，，
则，即，，
所以，
要证，即证时，，
即证，
因为，
只需证，即证，
即证，显然成立，
综上，有唯一极值点，且
【点睛】（1）对无法参变分离的恒成立问题，可进行分类讨论；
（2）函数的极值点问题，即导函数的零点问题，可结合导函数的单调性，特殊点的导函数值，及零点存在性定理进行证明.