2021-2022学年江西省临川第一中学暨临川一博中学高一下学期期中考试数学试题含解析

这是一份2021-2022学年江西省临川第一中学暨临川一博中学高一下学期期中考试数学试题含解析，共17页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
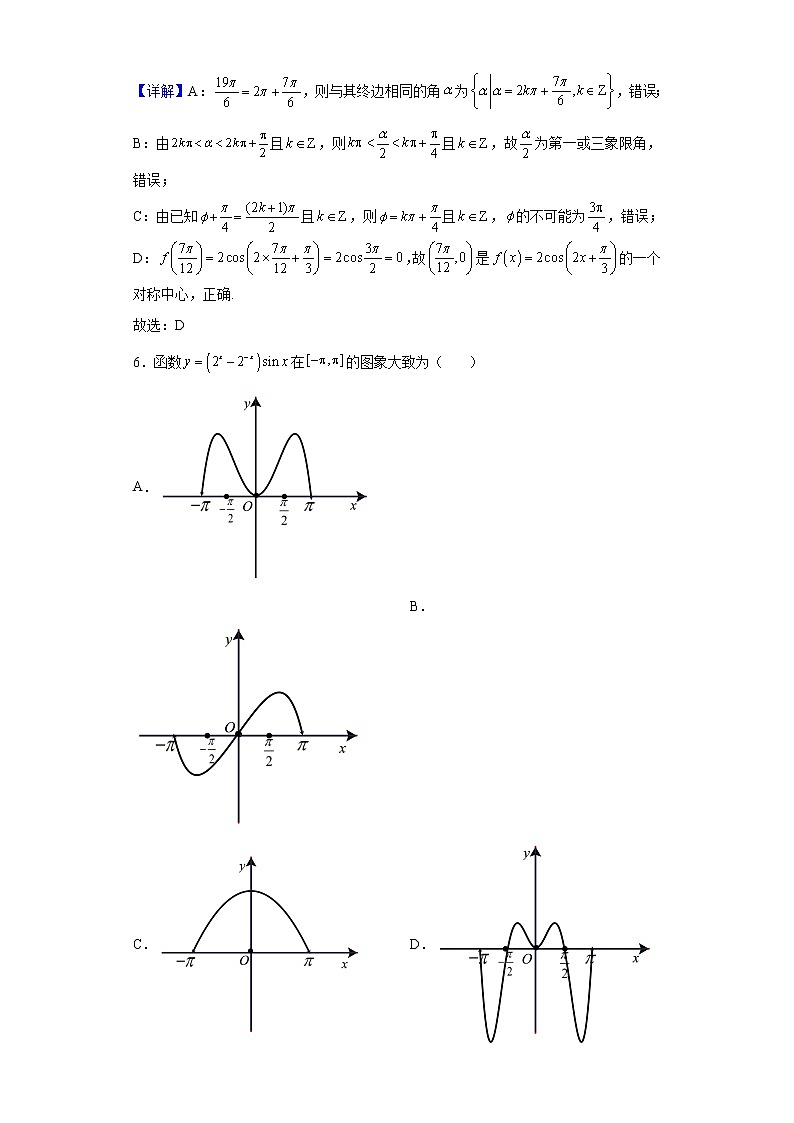
2021-2022学年江西省临川第一中学暨临川一博中学高一下学期期中考试数学试题一、单选题1．已知下列三角函数：①；②；③；④，其中值为正的是（       ）A．①② B．②③ C．①④ D．②④【答案】D【分析】根据三角函数的诱导公式和象限角的符号，这个判定，即可求解.【详解】①中，由于为第三象限角，所以；②中，由；③中，；④中，由于3为第二象限角，所以．故选：D.2．已知，则a､b､c的大小关系为（       ）A． B． C． D．【答案】C【分析】根据正弦函数、正切函数的性质计算可得；【详解】解：因为，在上单调递增，所以，即，，又，所以，所以；故选：C3．已知，，点P是线段MN上的点，且，则P点的坐标为（       ）A． B． C． D．【答案】A【分析】设出点P的坐标，利用向量的坐标运算结合相等向量，列式计算作答.【详解】设，则，，因，从而有，解得，所以P点的坐标为.故选：A4．在等腰梯形中，，，为的中点，则（       ）A． B．C． D．【答案】A【分析】作出示意图，利用数形结合，在梯形中，利用三角形法则即可求解.【详解】如图所示：在三角形中，.故选：A.5．下列说法正确的是（       ）A．与角终边相同的角的集合可以表示为B．若为第一象限角，则仍为第一象限角C．函数是偶函数，则的一个可能值为D．点是函数的一个对称中心【答案】D【分析】A写出其终边相同的角的集合判断；B由且，进而确定的范围，即可判断；C由三角函数的性质可得且，即可判断；D将点代入判断是否为对称中心即可.【详解】A：，则与其终边相同的角为，错误；B：由且，则且，故为第一或三象限角，错误；C：由已知且，则且，的不可能为，错误；D：，故是的一个对称中心，正确.故选：D6．函数在的图象大致为（       ）A． B．C． D．【答案】A【分析】根据函数解析式，结合特殊值，即可判断函数图象.【详解】设，则，故为上的偶函数，故排除B．又，，排除C、D．故选：A．【点睛】本题考查图象识别，注意从函数的奇偶性、单调性和特殊点函数值的正负等方面去判断，本题属于中档题.7．已知是边长为3的正方形内（包含边界）的一点，则的最大值是（       ）A．6 B．3 C．9 D．8【答案】C【解析】在正方形中建立如图的直角坐标系，设，结合向量数量积的概念可得结果.【详解】以点为原点建立如图所示的直角坐标系，设，，可得，，所以，，故，当时，最大，最大值为9，故选：C.【点睛】本题主要考查了向量数量积的最值问题，利用坐标法是解题的关键，属于基础题.8．在△ABC中，内角A，B，C所对边分别为a，b，c．若，AC＝4，，则（       ）A． B． C． D．【答案】D【分析】首先根据三角形面积公式和正余弦定理求得外接圆半径，然后结合正弦定理及和分比的性质求解.【详解】由三角形面积公式可得：，即，解得：c＝3，结合余弦定理可得：，则，由正弦定理有：，所以，结合和分比性质可得：．故选：D.二、多选题9．下列关于向量，，的说法错误的是（       ）A．若且，则B．当时，的充要条件是存在不全为零的实数，使得C．若，则D．，则【答案】ACD【分析】对于A、C：取，否定命题；对于B：利用向量共线定理直接判断；对于D：由，可得到，不一定有.即可判断.【详解】对于A：取，满足且，但是， 不一定平行.故A错误；对于B：由向量共线定理可得：当时，的充要条件是存在不全为零的实数，使得.故B正确.对于C：取，满足，但是，不一定相等.故C错误；对于D：因为，所以，展开，整理化简得：，所以，不一定有.故D错误；故选：ACD10．已知点是锐角三角形的外心，若，则的可能值是（       ）A． B． C． D．【答案】CD【分析】利用数量积的性质以及数量积的定义可以得到一个关于，的不等式，进而解出的取值范围，从而确定选项【详解】∵是锐角的外心，∴在三角形内部，不妨设锐角的外接圆的半径为，又，∴，可得，而．∴，∴或，如果则在三角形外部，三角形不是锐角三角形，∴，故选：CD．11．已知的内角、、所对的边分别为、、，下列四个命题中正确的命题是（       ）A．若，则一定是等边三角形B．若，则一定是等腰三角形C．若，则一定是等腰三角形D．若，则一定是锐角三角形【答案】AC【分析】对于A．利用正弦定理证明△ABC是等边三角形，故A正确；对于B，利用正弦定理化简得△ABC为等腰三角形或直角三角形，故B错误；对于C，利用正弦定理和三角恒等变换化简得△ABC是等腰三角形，故C正确；对于D，利用余弦定理化简得角C为锐角，但△ABC不一定是锐角三角形，故D错误．【详解】对于A．若，则，，即，即△ABC是等边三角形，故A正确；对于B，若，则由正弦定理得，，则或，即或，则△ABC为等腰三角形或直角三角形，故B错误；对于C，若，则即，则△ABC是等腰三角形，故C正确；对于D，△ABC中，∵，∴，所以角C为锐角，但△ABC不一定是锐角三角形，故D错误．故选：AC．12．水车在古代是进行灌溉引水的工具，是人类的一项古老的发明，也是人类利用自然和改造自然的象征．如图是一个半径为R的水车，一个水斗从点A(3，－3)出发，沿圆周按逆时针方向匀速旋转，且旋转一周用时60秒，经过t秒后，水斗旋转到点P，设点P的坐标为(x，y)，其纵坐标满足y＝f(t)＝Rsin(ωt＋φ)，则下列叙述正确的是（       ）A．R＝6，ω＝，φ＝－B．当t∈[35，55]时，点P到x轴的距离的最大值为6C．当t∈[10，25]时，函数y＝f(t)单调递减D．当t＝20时，|PA|＝6【答案】ABD【分析】根据题意及函数过点求出解析式判断A，由函数值域可判断B，根据正弦型函数的单调性可判断C，t＝20时求出P点，根据两点间距离公式判断D.【详解】由题意可知T＝60，所以＝60，解得ω＝，又从点A(，)出发，所以R＝6，6sin φ＝－3，又|φ|<，所以φ＝，故A正确；，当t∈[35，55]时，，则，，点到x轴的距离为，所以点到x轴的距离的最大值为6，故B正确；当t∈[10，25]时，，所以函数在[10，25]上不单调，故C不正确；当t＝20时，，则，且，所以P(0，6)，则，故D正确．综上，正确的是ABD.故选：ABD三、填空题13．若，则______．【答案】【分析】利用诱导公式化简可得结果.【详解】由题意得．故答案为：．14．已知非零向量， 且与的夹角为锐角，则实数λ的取值范围是_____【答案】【分析】先写出，再利用且与不共线求λ的取值范围即可.【详解】由题意知，，且与不共线，即且，解得且.故答案为：.15．奇函数的定义域为R，若为偶函数，且，则______．【答案】【分析】双对称性可以推出周期性，利用周期性改变自变量的大小，利用奇偶性调自变量的符号，即可求解【详解】由函数为偶函数可得，，又，故所以，即所以故该函数是周期为8的周期函数．又函数为奇函数，故，．所以．故答案为：16．已知函数，若在区间上的图象有且仅有2个最高点，则下面四个结论：①在上的图象有且仅有1个最低点；②在上至少有3个零点，至多4个零点；③在上单调递增；④的取值范围为；其中正确的所有序号是______．【答案】③④【分析】对于①②：作出符合题意的图像，利用图像否定结论；对于④：根据在区间上的图象有且仅有2个最高点，列不等式，解得的范围；对于③：利用复合函数的单调性法则进行判断.【详解】对于①：作出的图像如图所示：当图像如图2所示，符合题意，但是在上的图象有2个最低点.故①错误；对于②：当图像如图3所示，符合题意，但是在上有5个零点.故②错误；对于④：令，因为，所以，则.要使在区间上的图象有且仅有2个最高点，只需，解得：.故④正确；对于③：当时，.因为，所以，即落在内，所以在上单调递增. 故③正确；故答案为：③④四、解答题17．已知角的始边为轴的非负半轴，终边经过点，且 .（1）求实数的值；（2）若，求的值.【答案】（1）3或或0；（2）【分析】（1）根据三角函数的定义，列出关于的方程，即可求解.（2）由（1）得，求得，再由诱导公式化简，即可求解.【详解】（1）根据三角函数的定义可得，解得或或m=0（2）因为，所以，所以，又由诱导公式，可得.【点睛】本题主要考查了三角函数的定义，以及三角函数的诱导公式的化简求值，其中解答中熟记三角函数的定义，以及合理应用三角函数的诱导公式化简、运算是解答的关键，着重考查了运算与求解能力，属于基础题.18．已知向量，，．(1)若，求实数m，n的值；(2)若，求实数k的值．【答案】(1)(2)【分析】根据平面向量线性运算的坐标表示和相等向量的定义列出关于m、n的方程组，解之即可；(2)根据平面向量的坐标运算求出和的坐标，利用共线向量的坐标表示计算即可.【详解】(1)∵，，，，∴，所以，得；(2)∵，又，，∴，解得，故实数k的值为．19．在①图象过点，②图象关于直线对称，③图象关于点对称，这三个条件中任选一个，补充在下面问题中，并给出解答．问题：已知的最小正周期为，______．(1)求函数的解析式；(2)将的图象上所有点向左平移个单位长度，再将得到的图象上每个点的横坐标缩短到原来的（纵坐标不变），得到函数的图象，求的单调递增区间．【答案】(1)任选一条件，都有；(2).【分析】（1）若选①：由周期求出，根据 图象过点，求出 ，即得解；若选②：由周期求出，再根据函数图象的对称性求出 ，即得解； 若选③：由周期求出，根据对称中心求出，即得解. （2）解不等式即得解.【详解】(1)解：若选①：由已知得，则，于是，因为图象过点，所以，即，又因为，所以，故．若选②：由已知得，，则，于是．因为图象关于直线对称，所以，即，又因为，所以，故若选③：由已知得，则，于是．因为图象关于点对称，所以，即，又因为，所以，故(2)解：将的图象上所有点向左平移个单位长度，得到，再将得到的图象上每个点的横坐标缩短到原来的（纵坐标不变），得到，令，即，故的单调递增区间为．20．已知平面向量与满足，已知方向上的单位向量为，向量在向量方向上的投影向量为.(1)若与垂直，求的大小；(2)若与的夹角为，求向量与夹角的余弦值.【答案】(1)(2)【分析】（1）易知，得到，再根据与垂直求解；（2）由题意得，即，再利用平面向量的夹角求解.【详解】(1)解：由题意得，即，则.因为与垂直，所以，化简为，即，则.(2)由题意得，则，，，设向量与的夹角为，所以.21．如图所示，是某海湾旅游区的一角，其中，为了营造更加优美的旅游环境，旅游区管委会决定在直线海岸和上分别修建观光长廊和AC，其中是宽长廊，造价是元/米，是窄长廊，造价是元/米，两段长廊的总造价为120万元，同时在线段上靠近点的三等分点处建一个观光平台，并建水上直线通道（平台大小忽略不计），水上通道的造价是元/米．(1) 若规划在三角形区域内开发水上游乐项目，要求的面积最大，那么和的长度分别为多少米？(2) 在(1)的条件下，建直线通道还需要多少钱？【答案】（1）和AC的长度分别为750米和1500米（2）万元【详解】试题分析：（1）设长为米，长为米，依题意得，即，表示面积,利用基本不等式可得结论；（2）利用向量方法，将表示为，根据向量的数量积与模长的关系可得结果.试题解析：（1）设长为米，长为米，依题意得，即，                                                 = 当且仅当，即时等号成立，所以当的面积最大时，和AC的长度分别为750米和1500米（2）在(1)的条件下，因为．由                                           得                ，                                    元所以，建水上通道还需要万元．   解法二：在中，       在中，        在中，=   元所以，建水上通道还需要万元．        解法三：以A为原点，以AB为轴建立平面直角坐标系，则，,即，设 由，求得， 所以   所以， 元所以，建水上通道还需要万元．22．在中，角的对边分别为，已知.（1）求角的大小；（2）若，点满足，求的面积；（3）若，且外接圆半径为2，圆心为，为上的一动点，试求的取值范围.【答案】（1），（2），（3）【分析】（1）根据正弦定理和余弦定理，进行边角互化得，再利用余弦定理可求得，从而可求出角，（2）由余弦定理求出，再根据向量的线性运算可得,根据三角形的面积公式可求得答案，（3）由已知和余弦定理可得三角形为等边三角形，再运用向量的数量积运算可求得的范围【详解】（1）因为，所以由正弦定理和余弦定理得，化简得，所以由余弦定理得，，因为，所以，（2）由余弦定理得，，所以，即，所以，因为，所以，因为，所以，所以的面积为，（3）由，利用余弦定理得，得，所以三角形为等边三角形，所以，，,所以,所以,所以因为，所以，所以的取值范围为．