山东省济南市济阳区2022年数学一模试题及答案

这是一份山东省济南市济阳区2022年数学一模试题及答案，共24页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

 数学一模试题
一、单选题
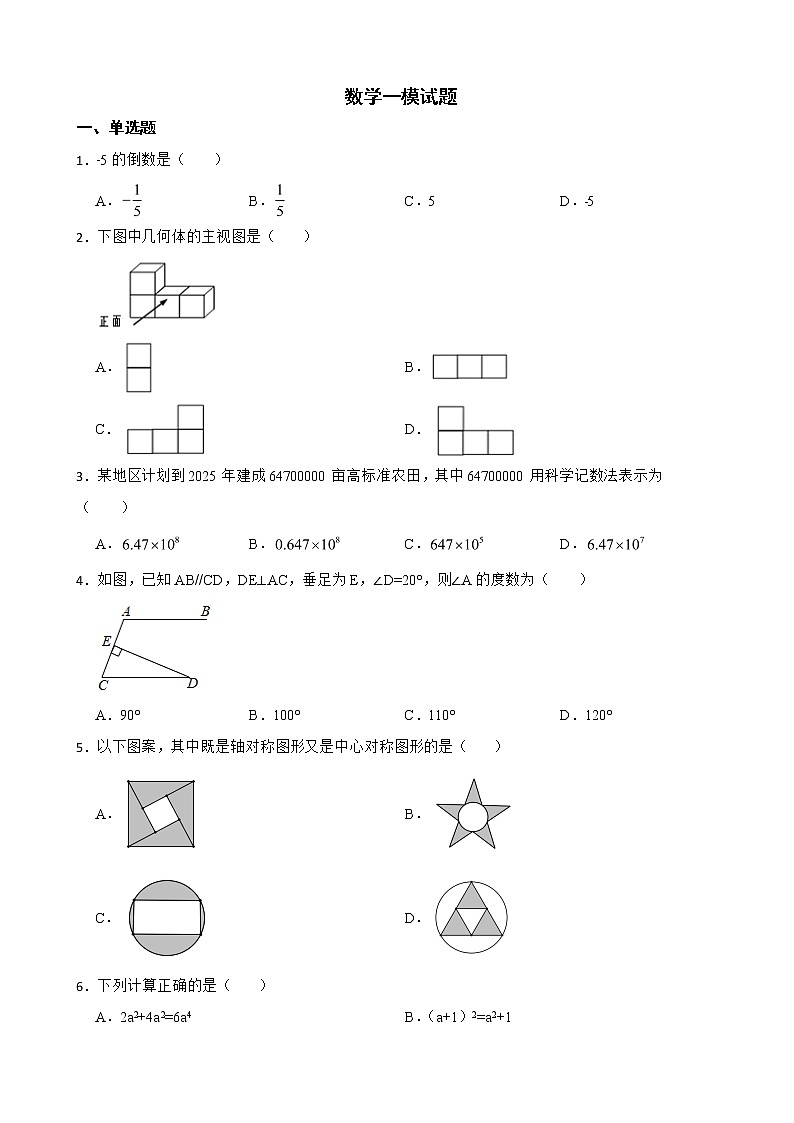
1．﹣5的倒数是（　　）
A． B． C．5 D．﹣5
2．下图中几何体的主视图是（　　）

A． B．
C． D．
3．某地区计划到2025年建成64700000亩高标准农田，其中64700000用科学记数法表示为（　　）
A． B． C． D．
4．如图，已知AB//CD，DE⊥AC，垂足为E，∠D=20°，则∠A的度数为（　　）

A．90° B．100° C．110° D．120°
5．以下图案，其中既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
6．下列计算正确的是（　　）
A．2a2+4a2=6a4 B．（a+1）2=a2+1
C．（a2）3=a5 D．x7÷x5=x2
7．化简的结果是（　　）
A． B． C． D．
8．某学校在手抄报活动中，济济和洋洋分别从抗击疫情，缅怀先烈，预防溺水三个专题中随机选择一个参加，两人恰好选择同一专题的概率是（　　）
A． B． C． D．
9．函数与函数y=kx+k在同一坐标系中的图象可能是（　　）
A． B．
C． D．
10．如图，热气球的探测器显示，从热气球A处看一栋楼顶部B处的仰角为36°，看这栋楼底部C处的俯角为60°，热气球A处与楼的水平距离为100m，则这栋楼的高度为（　　）（参考数据：≈1.73，tan36°≈0.73，sin36°≈0.59，cos36°≈0.81，结果保留整数）

A．232 m B．246 m C．254 m D．310 m
11．如图，在△ABC中，AB＝AC．在AB、AC上分别截取AP、AQ，使AP＝AQ．再分别以点P，Q为圆心，以大于PQ的长为半径作弧，两弧在∠BAC内交于点R，作射线AR，交BC于点D．已知BC＝5，AD=6．若点M、N分别是线段AD和线段AC上的动点，则CM+MN的最小值为（　　）

A．4 B．5 C． D．2
12．若二次函数y=a+bx+c（a≠0）的图象的顶点在第二象限，且过点（0，1）和（1，0），则m=a-b+c的值的变化范围是（　　）
A．0 二、填空题
13．因式分解：a2﹣6a+9=　 　．
14．在一次以“建设美丽济阳”为主题的演讲比赛中，小红的演讲内容、语言表达、演讲技能、形象礼仪的各项得分依次为9.5；9.4；9.2；9.7．若依次按40%，25%，25%，的比例确定她的综合得分，则她的综合得分是　 　．
15．如图，正五边形ABCDE中，内角∠EAB的角平分线与其内角∠ABC的角平分线相交于点P，则∠APB＝　 　度．

16．已知关于x的一元二次方程ax2﹣2x+c=0有两个相等的实数根，则﹣c+1的值等于　 　．
17．甲、乙两施工队分别从两端修一段长度为315米的公路．在施工过程中，甲队曾因技术改进而停工一天，之后加快了施工进度并与乙队共同按期完成任务．下表根据每天工程进度制作而成的．
施工时间/天
1
2
3
4
5
6
7
8
9
10
累计完成施工量/米
25
50
75
100
115
155
195
235
275
315
甲队技术改进后比技术改进前每天多修路　 　米．
18．如图，△ABC中，∠ABC=90°，AB=2，BC=4，点D是斜边AC的中点，将△DBC沿直线BD对折，C点落在E处，连接AE，则AE的长度为　 　．

三、解答题
19．计算： ．
20．解不等式组，并写出它的所有整数解
21．如图，已知四边形ABCD是平行四边形，BE⊥AC， DF⊥AC，求证：AE＝CF．

22．某校举行了冬奥会知识竞赛，在全校随机抽取了部分学生的竞赛成绩进行整理和分析（成绩得分用x表示，共分成四组），并绘制成如下的竞赛成绩分组统计表和扇形统计图． 其中“60≤x＜80”这组的数据如下：
61，74，68，62，73，70，72，78，69，74，79，68，74．
竞赛成绩分组统计表
组别
竞赛成绩分组
频数
1
60x<70
a
2
70x<80
b
3
80x<90
12
4
90x100
d
竞赛成绩扇形统计图

请根据以上信息，解答下列问题：
（1）填空：a=　 　；
（2）统计图中第四组对应圆心角为　 　度；
（3）“70≤x＜80”这组数据的众数是　 　 ，中位数是　 　；
（4）若学生竞赛成绩达到90分及以上获奖，请你估计全校1200名学生中获奖的人数．
23．如图，在△ABC中，，以AB为直径的分别交AC，BC于点D，E，过B点的圆的切线交AC的延长线于点F．

（1）求证：∠FBC=∠BAC；
（2）若，AD=6，求的半径的长．
24．某超市共用24000元同时购进甲、乙两种型号书包各200个，购进甲型号书包40个比购进乙型书包30个少用100元．
（1）求甲、乙两种型号书包的进价各为多少元?
（2）若超市把甲、乙两种型号书包均按每个90元定价进行零售，同时为扩大销售，拿出一部分书包按零售价的8折进行优惠销售．商场在这批背包全部售完后，若总获利不低于10200元，则超市用于优惠销售的书包数量最多为多少个?
25．如图，四边形AOBC是的正方形，D为BC中点，以O为坐标原点，OA，OB所在的直线为坐标轴建立平面直角坐标系，A点坐标（0，4），过点D的反比例函数y＝（k≠0）的图象与边AC交于E点，F是线段OB上的一动点．

备用图
（1）求k的值并直接写出点E的坐标；
（2）若AD平分∠CAF，求出F点的坐标；
（3）若△AFD的面积为S1，△AFO的面积为S2 ．若S1：S2=3：2，判断四边形AEFO的形状．并说明理由．
26．在直角△ABC中，∠ACB=90°，AC=3，BC=4，点D、E和F分别是斜边AB、直角边AC和直角边BC上的动点，∠EDF=90°，

（1）如图1，若四边形DECF是正方形，求这个正方形的边长．
（2）如图2，若E点正好运动到C点，并且tan∠DCF=，求BF的长．
（3）如图3，当时，求的值
27．抛物线过点A（－1，0），点B（3，0），与y轴交于C点．

（1）求抛物线的表达式及点C的坐标；
（2）如图1，设M是抛物线上的一点，若∠MAB=45°，求M点的坐标；
（3）如图2，点P在直线BC下方的抛物线上，过点P作PD⊥x轴于点D，交直线BC于点E，过P点作PF⊥BC，交BC与F点，△PEF的周长是否有最大值，若有最大值，求出此时P点的坐标．若不存在，说明理由．
答案解析部分
1．【答案】A
【解析】【解答】解：∵（-5）×（）=1，
∴﹣5的倒数是，
故答案为：A．

【分析】根据倒数的定义求解即可。
2．【答案】D
【解析】【解答】解：从正面可看到的几何体的左边有2个正方形，中间只有1个正方形，右边有1个正方形，
故答案为：D．

【分析】根据三视图的定义求解即可。
3．【答案】D
【解析】【解答】∵64700000=，
故答案为：D．

【分析】利用科学记数法的定义及书写要求求解即可。
4．【答案】C
【解析】【解答】∵DE⊥AC，∠D=20°，
∴∠C=70°，
∵AB//CD，
∴∠A+∠C=180°，
∴∠A=110°，
故答案为：C．

【分析】先利用三角形的内角和求出∠C=70°，再利用平行线的性质可得∠A=110°。
5．【答案】C
【解析】【解答】解：A．不是轴对称图形，是中心对称图形，此选项不符合题意；
B．是轴对称图形，不是中心对称图形，此选项不符合题意；
C．既是轴对称图形，又是中心对称图形，此选项符合题意；
D．是轴对称图形，不是中心对称图形，此选项不符合题意．
故答案为：C．

【分析】根据轴对称图形和中心对称图形的定义逐项判断即可。
6．【答案】D
【解析】【解答】解：A、2a2+4a2=6a2，所以A选项不正确；
B、（a+1）2=a2+2a+1，所以B选项不正确；
C、（a2）5=a10，所以C选项不正确；
D、x7÷x5=x2，所以D选项正确．
故选D．
【分析】根据合并同类项对A进行判断；根据完全平方公式对B进行判断；根据幂的乘方法则对C进行判断；根据同底数幂的除法法则对D进行判断．
7．【答案】A
【解析】【解答】解：，
故答案为：A．

【分析】利用分式的除法运算法则求解即可。
8．【答案】A
【解析】【解答】解：画树状图为：（用A、B、C分别表示“抗击疫情，缅怀先烈，预防溺水”三个专题）

共有9种等可能的结果数，其中两人恰好选择同一专题的结果数为3，
所以两人恰好选择同一专题的概率==．
故答案为：A．

【分析】先利用树状图求出所有等可能的情况数，再利用概率公式求解即可。
9．【答案】C
【解析】【解答】解：A、由反比例函数的图象在一、三象限可知，k＞0，
∴一次函数y＝−kx＋k的图象经过一、二、四象限，故本选项不符合题意；
B、由反比例函数的图象在二、四象限可知，k＜0，
∴一次函数y＝−kx＋k的图象经过一、三、四象限，故本选项不符合题意；
C、由反比例函数的图象在二、四象限可知，k＜0，
∴一次函数y＝−kx＋k的图象经过一、三、四象限，故本选项符合题意；
D、由反比例函数的图象在一、三象限可知，k＞0，
∴一次函数y＝−kx＋k的图象经过一、二、四象限，故本选项不符合题意．
故答案为：C．

【分析】根据反比例函数和一次函数的图象与系数的关系逐项判断即可。
10．【答案】B
【解析】【解答】解：如图，过点作于点，

由题意得：，
则在中，，
在中，，
所以这栋楼的高度为，
故答案为：B．

【分析】过点作于点，先利用解直角三角形的方法求出CD和BD的长，再利用线段的和差可得。
11．【答案】C
【解析】【解答】解：连接BM，
根据题中作图可知，AD平分，
，
，，
，
，
过点B作于点E，则的最小值即为BE的长度，

，
，
，
∵，
，
即，
解得：，
故答案为：C．

【分析】过点B作于点E，则的最小值即为BE的长度，由，得出，代入计算即可。
12．【答案】B
【解析】【解答】∵二次函数y=a+bx+c（a≠0）的图象的顶点在第二象限，且过点（0，1）和（1，0），
∴点（0，1）和（1，0）都在对称轴的右侧，＜0，c=1，a+b+c=0，
∵0＜1，1＞0，
∴在对称轴的右侧，y随x的增大而减小，
∴a＜0，b＜0，
∴a= -b-1＜0，-b＞0，a+c= -b，
∴0＜-b＜1，
∴0＜-2b＜2，
∵m=a-b+c=-2b，
∴0 故答案为：B．

【分析】将已知两点坐标带入二次函数解析式，得出c的值以及a、b的关系式，带入消元，再根据对称轴的位置判断m的取值范围即可。
13．【答案】（a﹣3）2
【解析】【解答】解：a2﹣6a+9=（a﹣3）2．
【分析】本题是一个二次三项式，且a2和9分别是a和3的平方，6a是它们二者积的两倍，符合完全平方公式的结构特点，因此可用完全平方公式进行因式分解．
14．【答案】9.42
【解析】【解答】解：综合得分是：，
故答案为：9.42．

【分析】利用加权平均数的计算方法求解即可。
15．【答案】72
【解析】【解答】解：∵五边形ABCDE为正五边形，
∴∠EAB=∠ABC==108度，
∵AP是∠EAB的角平分线，
∴∠PAB=54度，
∵BP是∠ABC的角平分线，
∴∠ABP=54°．
∴∠APB=180°-54°-54°=72°，
故答案为：72．

【分析】先利用正多边形的性质求出∠EAB=∠ABC==108度，再利用角平分线的定义可得∠ABP=∠PAB=54°，最后利用三角形的内角和可得∠APB=180°-54°-54°=72°。
16．【答案】1
【解析】【解答】解：根据题意得：
△，
解得：，
∵方程ax2-2x+c＝0是一元二次方程，
∴a≠0，
等式两边同时除以a得：，
则．
故答案为1．

【分析】利用一元二次方程根的判别式列出方程可得，所以，再将其代入 ﹣c+1计算即可。
17．【答案】15
【解析】【解答】解：由表格可得，第5天甲队停工，
甲队技术改进前两队每天修路50－25＝25（米），
甲队技术改进后两队每天修路155－115＝40（米），
∴甲队技术改进后比技术改进前每天多修路40－25＝15（米），
故答案为：15．

【分析】先根据第4、5两天的施工量，求出乙每天修路15米，再根据第2、3两天施工量，求出甲技术改进前每天修路10米，再根据第5、6两天的施工量，求出甲队技术改进后每天修路25米，最后求出甲队技术改进后比技术改进前每天多修路的米数即可。
18．【答案】
【解析】【解答】解：如图，连接CE，延长BD交CE于F，过点E作EG⊥AC于G，

由折叠可知，点C与点E关于直线BD对称，
∴CD=DE，BE=BC=4，EF=CF，DF⊥CE，
在Rt△ABC中，由勾股定理，得
AC=，
∵点D是斜边AC的中点，
∴BD=CD=AC=，
∴DE=CD=，
在Rt△EFD中，由勾股定理，得
EF=，
在Rt△EFB中，由勾股定理，得
EF==，
∴5-DF2=42-（+DF）2，
解得：DF=，
∴CF=EF=，
∴CE=，
∵∠CGE=∠CFD=90°，∠ECG=∠DCF，
∴△ECG∽△DCF，
∴，即，
∴EG=，CG=，
∴AG=AC-CG=，
在Rt△AEG中，由勾股定理，得
AE==．
故答案为：．

【分析】连接CE，延长BD交CE于F，过点E作EG⊥AC于G，由折叠可知，点C与点E关于直线BD对称，得出CD=DE，BE=BC=4，EF=CF，DF⊥CE，在Rt△ABC中，由勾股定理，得AC的值，在Rt△EFD中，由勾股定理，得出EF的值，代入计算得出CE的值，证出△ECG∽△DCF，推出AG=AC-CG，在Rt△AEG中，由勾股定理得出AE的值即可。
19．【答案】解：



【解析】【分析】分别计算负整数指数幂，锐角三角函数，绝对值，零次幂，再合并即可．
20．【答案】解：
解不等式① 得 x≥－1，
解不等式② 得 x＜3，
所以原不等式组的解集为：－1≤x＜3，
它的所有整数解为－1，0，1，2．
【解析】【分析】利用不等式的性质及不等式组的解法求出解集即可。
21．【答案】证明：∵四边形ABCD是平行四边形
∴AB=CD，ABCD
∴∠BAC=∠DCA
∵BEAC于E，DFAC于F
∴∠AEB=∠DFC=90°
在ABE和CDF中 ，

∴ABECDF（AAS）
∴AE=CF
【解析】【分析】根据平行四边形的性质，再利用“AAS”证明ABECDF，即可得到AE=CF。
22．【答案】（1）5
（2）135
（3）74；74
（4）解：×1200＝450（人）
答：估计全校获奖人数为450人．
【解析】【解答】（1）解：在61，74，68，62，73，70，72，78，69，74，79，68，74这组数据中，成绩在60x<70的有：61，68，62，69，68这5个数据，即a=5，
故答案为：5．
（2）解：在61，74，68，62，73，70，72，78，69，74，79，68，74这组数据中，成绩在70x<80的有8个数据，所以b=8，
抽取的学生总人数为：（人）
d=40-5-8-12=15，
第四组对应圆心角度数为：
故答案为：135°．
（3）解：“70≤x＜80”这组的数据如下：
74，73，70，72，78，74，79，74
将这组数据按从小到大的顺序排列如下：70，72，73，74，74，74，78，79
众数为：74，中位数为：
故答案为：74，74．

【分析】（1）根据60x<70这组的数据即可求出a的值；
（2）由3组的人数除以所占百分比得出抽取的总数，总数减去1、2、3组的人数，即可得出第4组的人数占由360度乘第4组所占的比例即可；
（3）根据众数、中位数的意义即可求解；
（4）利用样本估计总体求解即可。
23．【答案】（1）证明：连接AE，

∵AB是⊙O的直径，
∴AE⊥BC，
∵AB＝AC，
∴∠BAE＝∠BAC，
∵FB是⊙O的切线，
∴AB⊥BF，
∵AE⊥BC，
∴∠BAE＋∠ABE＝90°，
∵AB⊥BF，
∴∠FBC＋∠ABE＝90°，
∴∠BAE＝∠FBC，
∴∠FBC＝∠BAC；
（2）解：连接BD，

∵AB是⊙O的直径，
∴AD⊥DB，
∴∠BFA＋∠FBD＝90°，
∵AB⊥BF，
∴∠FBD＋∠ABD＝90°，
∴∠BFA＝∠ABD，
∵tan∠BFA=，
∴tan∠ABD=，
∵tan∠ABD＝，
∴＝，
∵AD＝6，
∴BD＝8．
∴由勾股定理得：AB＝10．
∴的半径的长为5．
【解析】【分析】（1）连接AE，根据圆周角定理得出∠BAE＋∠ABE＝90°，再证明∠BAE＝∠FBC，从而得出结论；
（2）连接BD，根据圆周角定理得出∠FBD＋∠ABD＝90°，再证明∠BFA＝∠ABD，利用正切的定义得出BD＝8，由勾股定理得AB的值即可。
24．【答案】（1）解：设A、B两种型号书包的进货单价各为x元、y元，
由题意得，，
解得：，
答：A、B两种型号书包的进货单价各为50元、70元；
（2）解：设商场用于优惠销售的书包数量为a个，
由题意得，90×（400-a）＋90×0.8a-24000≥10200，
解得：a≤100．
答：商场用于优惠销售的书包数量最多为100个．
【解析】【分析】（1）设A、B两种型号书包的进货单价各为x元、y元，根据题意列出方程求解即可；
（2）设商场用于优惠销售的书包数量为a个，根据题意列出不等式90×（400-a）＋90×0.8a-24000≥10200求解即可。
25．【答案】（1）解：∵A点坐标（0，4），
∴C点坐标（4，4），
∵D为BC中点，
∴D点坐标（4，2），
∴k＝4×2＝8，
∴反比例函数解析式为y＝，
当y＝时，x＝2，
∴E（2，4）；
（2）解：延长AD交x轴于G点，如图1，
∵AC∥OB，
∴∠DAC＝∠BGD，
又∵CD＝BD，∠C＝∠DBG＝90°，
∴△BDG ≌△CDA（AAS），
∴BG＝AC＝4，
∴OG＝OB＋BG＝8，
∵DA平分∠CAF，
∴∠CAD＝∠GAF，
∴∠GAF＝∠DGB，
∴AF＝FG，
设OF＝m，则AF＝FG＝8－m，
∵OA2＋OF2＝AF2，
∴42＋m2＝（8－m）2，
∴m＝3
∴F点的坐标为（3，0）；
（3）解：四边形AEFO是矩形．
理由：如图1，设△AFG的面积的为s3，

∵AD＝DG，
∴s3＝2s1，
∵S1：S2＝3：2，
∴s3：s2＝3：1，
∴FG：FO＝3：1，
∵OG＝8，
∴FO＝OG＝2，
∵AE＝2，
∴FO＝AE，
又∵FO∥AE，
∴四边形AEFO是平行四边形，
∵∠AOF＝90°，
∴四边形AEFO是矩形．
【解析】【分析】（1）先求出D点坐标代入解析式即可；
（2）证出△BDG ≌△CDA（AAS），BG＝AC＝4，AF＝FG，设OF＝m，则AF＝FG＝8－m，由勾股定理可求解；
（3）设△AFG的面积的为s3，得出四边形AEFO是平行四边形，即可求解。
26．【答案】（1）解：∵四边形AOBC是的正方形，
∴DEBC，
∴AE：AC＝DE：BC
设正方形的边长为x，则AE＝3－x，
∴（3－x）：3＝x：4，
解得 x＝，
即这个正方形的边长为；
（2）解：过D点作DG⊥BC，垂足为G点，如图2，

∵tan∠DCF＝，
∴DG：CG＝1：2
设DG＝y，则CG＝2y，
∴BG＝4－2y，
∵DGAC，
∴DG：AC＝BG：BC，
∴y：3＝（4－2y）：4，解得 y＝1.2 ，
BG＝4－2y＝1.6，
∵∠EDF＝，
∴∠CDG＋∠GDF＝，
∵DG⊥BC，
∴∠CDG＋∠DCG＝，
∴∠GDF＝∠DCG，
∵tan∠DCF＝，
∴tan∠GDF＝，
∴，
∵DG＝1.2，
∴FG＝0.6，
∴FB＝BG－FG＝1.6－0.6 ＝1；
（3）解：过D点作DM⊥AC，垂足为M点，过D点作DN⊥BC，垂足为N点，如图3，

∵∠ACB＝，AC＝3，BC＝4，
∴AB＝5，
∵DM⊥AC，DN⊥BC，∠ACB＝，
∴∠MDN＝，
∴∠MDE＋∠EDN＝，
∵∠EDF＝，
∴∠FDN＋∠EDN＝，
∴∠MDE＝∠FDN，
∴Rt△DME∽Rt△DNF，
∴＝，
∵=，
∴=，
设DM＝z，则DN＝2z，
∵DMBC ，
∴DM：BC＝AM：AC＝AD：AB，
∴z：4＝（3－2z）：3，解得 z＝，
∴：4＝AD：5 ，
∴AD＝，BD＝5－＝，
∴＝．
【解析】【分析】（1）根据正方形的性质得出DEBC，AE：AC＝DE：BC，设正方形的边长为x，则AE＝3－x，代入计算即可；
（2）设DG＝y，则CG＝2y，得出BG＝4－2y，代入计算即可；
（3）证出Rt△DME∽Rt△DNF，设DM＝z，则DN＝2z，由平行线的性质得出DM：BC＝AM：AC＝AD：AB，代入计算即可。
27．【答案】（1）解：由题意得
，
解得，
∴抛物线的解析式为，
∴点C（0，－3）．
（2）解：①当M点在第一象限时，

设M（m，），
过M点作MN⊥x轴，
∵∠MAB＝45°，MN＝NA，
∴m＋1＝，
解方程得：m＝4或m＝－1，
m＝－1不合题意，舍去．
故m＝4 ，
∴M（4，5）；
当M点在第四象限时，同理可得：
m＋1＝－（）
解方程得：m＝2或m＝－1，
m＝－1不合题意，舍去．
故m＝2，
∴M（2，－3），
综上M（4，5）或M（2，－3）．
（3）解：△PEF的周长有最大值．理由如下：
∵PD⊥DB，
∴∠EBD＝90°－∠DEB，
∵PF⊥BC，
∴∠FPE＝90°－∠FEP，
∵∠DEB＝∠FEP，
∴∠EBD＝∠FPE，
又∵∠EFP＝∠BOC＝90°，
∴△FPE∽△OBC，
∴△PEF的周长：△OBC的周长＝PE：BC，
∵OB=OC=3，
∴BC=，
∴△PEF的周长为z，△OBC的周长＝，
∵直线BC过B（3，0）和C（0，－3），
设直线BC的解析式为y=px+q，
∴，
解得，
∴直线BC的解析式为y＝x－3，
设P（n，），则E（n，n－3）
PE＝n－3－（）＝，
∴z：（6＋3）＝（）：3，
z＝－（＋1） ＋3（＋1）n，
∵－（＋1）＜0，
∴z有最大值，此时n＝，
当n＝时，＝－，
故P点的坐标为（，－）．
【解析】【分析】（1）利用待定系数法即可求出二次函数解析式；
（2）当M点在第一象限时，当M点在第四象限时，分两种情况即可得解；
（3）先利用待定系数法求出直线BC的解析式，设P（n，），则E（n，n－3），由－（＋1）＜0，得出z有最大值，此时n＝，当n＝时，＝－，即可得出P点的坐标。