2021河北省正定中学高三上学期第一次半月考数学试题含答案

河北正定中学2021届高三年级第一次半月考

数学试题

(考试时间:120分钟  分值:150分)

一．选择题(本题共12小题，每小题5分，共60分，1-8为单选题，9-12为多选题)

1.已知，是两条不同的直线，，是两个不同的平面，给出下列命题：

①若，，则；        ②若，，则；

③若，，，则； ④若，，则．

其中所有正确命题的序号是　　

A．①② B．②③ C．②④ D．①④

2.在空间四边形的各边，，，上依次取点，，，，若、所在直线相交于点，则　　

A．点必在直线上             B．点必在直线上 

C．点必在平面外            D．点必在平面内

3.若正四面体的每条棱长均为2，则二面角的余弦值为　　

A． B． C． D．

4.如图，四边形中，，，．将四边形沿对角线折成四面体，使平面平面，则下列结论正确的是　　

A． 

B． 

C．与平面所成的角为 

D．四面体的体积为

5.在等差数列中，前项和为，若，，且，则在数列中　　

A．最大值是 B．最小值是 C．最大值是 D．最小值是

6.直三棱柱中，，，为的中点．异面直线与所成角的余弦值是　　

A． B． C． D．

7．如图，二面角的大小是，线段．，与所成的角为．直线与平面所成的角的正弦值是　　

A．     B．         C．    D．

8．已知数列满足，，则的最小值是　　

A．0 B． C．1 D．

9．（多选题）已知数列的前项和为，，，数列的前项和为，则下列选项正确的为　　

A．数列是等差数列                   

B．数列是等比数列 

C．数列的通项公式为       

D．

10．（多选题）如图，正方体的棱长为，线段上有两个动点，，且，以下结论正确的有　　

A． 

B．点到平面的距离为定值 

C．三棱锥的体积是正方体体积的 

D．异面直线，所成的角为定值

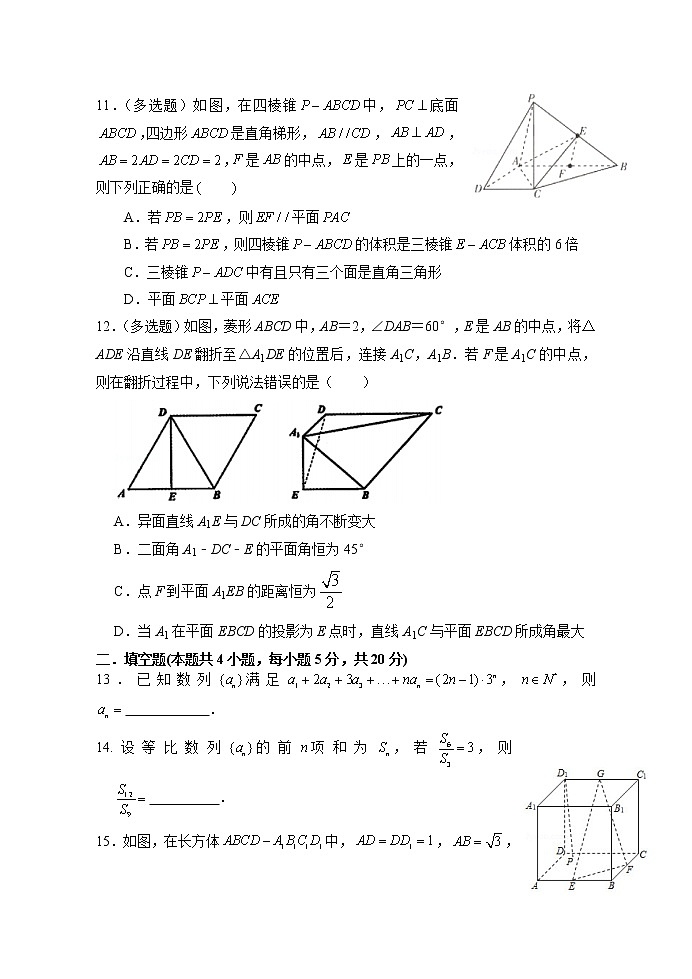
11．（多选题）如图，在四棱锥中，底面，四边形是直角梯形，，，，是的中点，是上的一点，则下列正确的是　　

A．若，则平面 

B．若，则四棱锥的体积是三棱锥体积的6倍 

C．三棱锥中有且只有三个面是直角三角形    

D．平面平面

12．（多选题）如图，菱形ABCD中，AB＝2，∠DAB＝60°，E是AB的中点，将△ADE沿直线DE翻折至△A1DE的位置后，连接A1C，A1B．若F是A1C的中点，则在翻折过程中，下列说法错误的是（　　）

A．异面直线A1E与DC所成的角不断变大 

B．二面角A1﹣DC﹣E的平面角恒为45° 

C．点F到平面A1EB的距离恒为 

D．当A1在平面EBCD的投影为E点时，直线A1C与平面EBCD所成角最大

二．填空题(本题共4小题，每小题5分，共20分)

13．已知数列满足，，则　　      　．

14.设等比数列的前项和为，若，则　      　．

15．如图，在长方体中，，，，，分别为，，的中点．点在平面内，若直线平面，则线段长度的最小值是　　      　．

16.已知三棱锥的棱长均为6，其内有个小球，球与三棱锥的四个面都相切，球与三棱锥的三个面和球都相切，如此类推，，球与三棱锥的三个面和球都相切，则球的体积等于　     　，球的表面积等于　      　．

三．解答题（本题共6小题，共70分）

17．（本小题10分）

在①，②，，③这三个条件中任选一个补充在下面的问题中，并加以解答．

设等差数列的前项和为，数列为等比数列，_____，．求数列的前项和．

18．（本小题12分）

如图，在多面体中，四边形是边长为2的正方形，平面，平面，且，与交于点．

（1）在棱上找一点，使平面，给出证明并求的长；

（2）求三棱锥的体积．

19．（本小题12分）

如图，在矩形中，是的中点，以为折痕将向上折起，使为，且平面平面．

（Ⅰ）求证：；

（Ⅱ）求直线与平面所成角的正弦值．

20．（本小题12分）

已知各项均为正数的数列的前项和为，且满足，，，各项均为正数的等比数列满足，．

（1）求数列，的通项公式；

（2）若，数列的前项和；

①求；

②若对任意，，均有恒成立，求实数的取值范围．

21．（本小题12分）

如图，四棱锥的底面为矩形，，，点在底面上的射影在上，是的中点．

（1）证明：平面

（2）若，且与面所成的角的正弦值为，求二面角的余弦值．

22．（本小题12分）

如图，是以为直径的圆上异于，的点，平面平面，，，，分别是，的中点，记平面与平面的交线为直线．

（Ⅰ）求证：直线平面；

（Ⅱ）直线上是否存在点，使直线分别与平面、直线所成的角互余？若存在，求出的值；若不存在，请说明理由．

河北正定中学2021届高三年级第一次半月考答案

1．【解答】解：由，是两条不同的直线，，是两个不同的平面，知：

对于①，若，，则由线面垂直的性质和线面平行的性质得，故①正确；

对于②，若，，则或，故②错误；

对于③，若，，，则与相交、平行或异面，故③错误；

对于④，若，，则由面面垂直的性质定理得，故④正确．故选：．

2．【解答】解：如图：连接、、，、所在直线相交于点，

且，平面，平面，平面，且平面，由平面平面，，故选：．

3.【解答】解：在正四面体中，取的中点，连接，，

如图所示由于和都为等边三角形，为的中点，

所以，，所以为两项邻面和平面的平面角，

由于四面体的各棱长为2，故利用勾股定理得到，

故在中，，故选：．

4．【解答】解：若成立可得，产生矛盾，故不正确；

由题设知：△为等腰△，平面，得平面，于是正确；

由与平面所成的角为知不正确；，不正确．故选：．

5.【解答】解：，即

整理得，

数列的前7项为负，故数列中最小值是故选：．

6.【解答】解：直三棱柱中，，，为的中点．以为原点，为轴，为轴，为轴，建立空间直角坐标系，设，则，0，，，2，，，0，，，0，，，2，，，0，，设异面直线与所成角为，

则．异面直线与所成角的余弦值为．故选：．

7．【解答】解：过点作平面的垂线，垂足为，在内过作的垂线．垂足为连接，有三垂线定理可知，故为二面角的平面角，为又由已知，

连接，则为与平面所成的角设，则，，

直线与平面所成的角的正弦值．故选：．

8．【解答】解：，两边同时除以，得

，，

故，故最小值为时，的最小值是1故选：．

9．【解答】解：由即为，

可化为，由，可得数列是首项为2，公比为2的等比数列，

则，即，又，

可得，

故错误，，，正确．故选：．

10.【解答】解：对于，根据题意，，，平面，

所以，所以正确；对于，到平面的距离是定值，所以点到的距离为定值，则正确；对于，三棱锥的体积为，三棱锥的体积是正方体体积的，正确；

对于，异面直线，所成的角为定值，命题错误；故选：．

11.【解答】解：在中，是的中点，是上的一点，若，则，

又平面，平面，平面，故正确；在中，若，

则四棱锥的体积，

三棱锥体积为：，

四棱锥的体积是三棱锥体积的3倍，故错误；

在中，三棱锥中，，，，是直角三角形，故错误；

在中，，，平面，，

，平面，平面，平面平面，故正确．故选：．

12.【解答】解：对于A，因为 DC∥EB，所以异面直线 A1E 与 DC 所成角即为∠A1EB 或其补角，在翻折过中，异面直线A1E与DC 所成角是先增大后减小，所以A不正确；

对于B，二面角A1﹣DC﹣E 的平面角不是定值，所以B不正确；

对于C，因为F是AC 的中点，所以点 F 到平面A1EB 的距离是点C 到平面A1EB的距离的，

因为 DC∥EB，DC⊄平面A1EB，EB⊂平面A1EB，所以DC∥平面A1EB，

所以点C到平面A1EB 的距离与点D 到平面A1EB 的距离相等，

又DE⊥EB，DE⊥EA1，EA∩EB＝E，所以DE⊥平面A1EB，

易知 DE＝，所以点F到平面 A1EB 的距离为，所以C正确；

对于D，因在平面 A1EB 中，作 A1H⊥EB，垂足为H，则A1H⊥平面DEBC，直线A1C与平面DEBC 所成角为∠A1CH，在平面 A1EB 中，点A1的运动轨迹在以E为圆心，半径为A1E的圆上，当且仅当A1E⊥A1B时此时直线A1C与平面DEBC所成角最大，所以D不正确；故选：ABD．

13．【解答】解：当时，由，，

得，

两式作差得，

则，当时，，不满足，，

14.【解答】解：为等比数列，则，，，也成等比数列，

由，令则，则由，，，也成等比数列，

可得，，则．

15．【解答】解：如图，连结，，，，，分别为，，的中点，

，平面，平面，平面，，平面，平面，平面，，平面平面，平面，

点在直线上，在中，，，，，

当时，线段的长度最小，最小值为．故答案为：．

16.【解答】解：如图，设球半径为，，球的半径为，为中点，球与平面、切于、，球与平面切于，作截面，设正四面体的棱长为由平面几何知识可得，解得，同时，解得，把代入的，，由平面几何知识可得数列是以为首项，公比为的等比数列，所以，故球的体积；

球的表面积，故答案为；

17．【解答】解：选①：当时，，当时，，又满足，所以．设的公比为，又因为，得，，所以；

由数列的前项和为，又可知，

数列的前项和为，

故．

选②：设公差为，由解得

所以．设的公比为，又因为，得，，所以．由数列的前项和为，又可知，数列的前项和为，故．

选③：由，，所以，所以．设的公比为，又因为，得．

由数列的前项和为，又可知，

数列的前项和为，故．

18．【解答】解：（1）当时，有平面．证明如下：平面，平面，，，又，在中，，又平面，平面，平面．又，．

（2）由（1）得，，．

三棱锥的体积为．

19.解（Ⅰ）在中，，在中，，

∵，∴．∵平面平面，且交线为，∴平面．∵平面，

∴．

（Ⅱ）设与相交于点，由（Ⅰ）知，

∵，∴平面，∵平面，

∴平面平面，且交线为，

如图6－2，作，垂足为，则平面，

连结，则是直线与平面所成的角．

由平面几何的知识可知，∴．

在中，，

在中，，可求得．∴．

∴直线与平面所成的角的正弦值为．

20．【解答】解：（Ⅰ）因为，所以，

两式相减得：，即，又因为数列的各项均为正数，

所以，又因为，，即，

所以当时上式成立，即数列是首项为1、公差为3的等差数列，

所以；因为，，所以；

（Ⅱ）由可知．

①，

，

两式相减，得：，

所以；

②由①可知若对任意，，均有恒成立，

等价于恒成立，

所以，即恒成立，

设，则，

所以当时，当时，

所以当的最大值为，故，

即实数的取值范围是：，．

21.【解答】解：（1）在矩形中，，且是的中点，

，（1分），

，，即．（3分）

由题可知面面，且交线为，面．（5分）

（2）：令与交于点，，且是的中点，．

面面，面．

取中点，连接，，因为底面为矩形，所以．建立如图所示的空间直角标系：

，，，，，，，，，，0，，（6分）

设面的法向量为，

由，

令，面的法向量为

由与面所成的角的正弦值为，

，

设平面的法向量为，，

由 令

设平面的法向量为，

由，令 （10分）

 二面角的余弦值为     （12分）

22.【解答】（Ⅰ）证明：，分别是，的中点，，

又平面，不包含于平面，面，又面，面面，

，又，面面，面面，面，面．

（2）解：以为坐标原点，为轴，为轴，过垂直于面的直线为轴，建立空间直角坐标系，，0，，，4，，，0，，，，

，，

设，，，面的法向量为，则，

取，得，，

，，

依题意，得，

．直线上存在点，使直线分别与平面、直线所成的角互余，．