2022安徽省江淮十校高三上学期第一次联考文科数学试题含答案

江淮十校2022届高三第一次联考

 数学（文科） 2021.8

注意事项：

1.本试卷满分150分，考试时间120分钟。

2.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

3.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

4.考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.

1.复数在复平面上对应的点在（    ）

A.第一象限 B.第二象限 C.第三象限 D.第四象限

2.已知集合，，则等于（    ）

A. B. C. D.

3.已知双曲线C：，则该双曲线的离心率为（    ）

A. B. C.2 D.4

4.“”是“直线与直线平行”的（    ）

A.充分不必要条件  B.必要不充分条件

C.充要条件  D.既不充分也不必要条件

5.设函数，若，则（    ）

A. B. C.1 D.2

6.已知两个等比数列，的前n项积分别为，，若，则（    ）

A.3 B.27 C.81 D.243

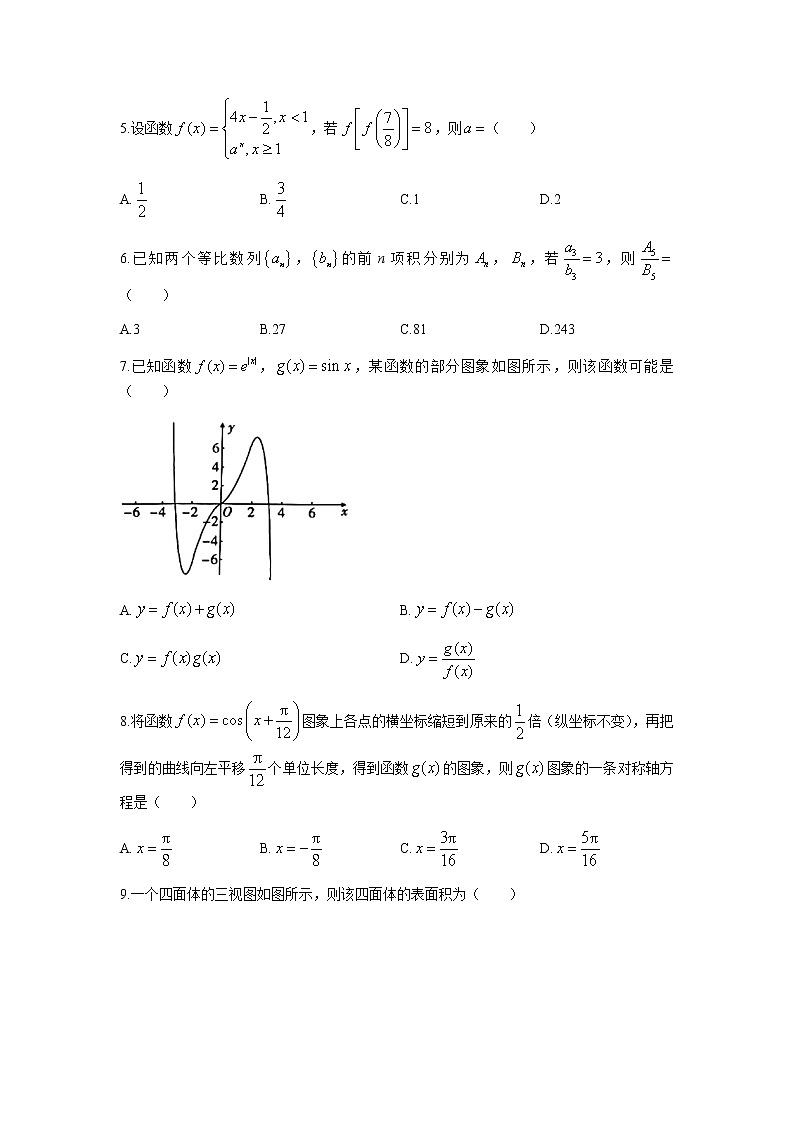
7.已知函数，，某函数的部分图象如图所示，则该函数可能是（    ）

A.  B.

C.  D.

8.将函数图象上各点的横坐标缩短到原来的倍（纵坐标不变），再把得到的曲线向左平移个单位长度，得到函数的图象，则图象的一条对称轴方程是（    ）

A. B. C. D.

9.一个四面体的三视图如图所示，则该四面体的表面积为（    ）

A. B. C. D.

10.我国古代以天为主，以地为从，天和干相连叫天干，地和支相连叫地支，合起来叫天干地支.天干有十个，就是甲、乙、丙、丁、戊、己、庚、辛、壬、癸，地支有十二个，依次是子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.古人把它们按照甲子、乙丑、丙寅……的顺序而不重复地搭配起来，从甲子到癸亥共六十对，叫做一甲子.我国古人用这六十对干支来表示年、月、日、时的序号，周而复始，不断循环，这就是干支纪年法（即农历）.干支纪年历法，是屹立于世界民族之林的科学历法之一.今年（2021年）是辛丑年，也是伟大的中国共产党成立100周年，则中国共产党成立的那一年是（    ）

A.辛酉年 B.辛戊年 C.壬酉年 D.壬戊年

11.的内角A，B，C的对边分别为a，b，c，若，，则面积的最大值为（    ）

A. B. C.1 D.2

12.若，恒成立，则a的最大值为（    ）

A. B.1 C. e D.

二、填空题：本题共4小题，每小题5分，共20分.

13.若x，y满足约束条件，则的最大值为____________.

14.在中，已知点D满足，若，则____________.

15.已知点P为抛物线C：上的动点，过点P作圆M：的一条切线，切点为A，则的最小值为____________.

16.已知正方体的棱长等于1，点为P底面的四条棱上的动点，则的取值范围为____________.

三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.

17.（10分）已知函数.

（1）求的单调递减区间；

（2）设锐角内角A，B，C的对边分别为a，b，c，已知，，求b的取值范围.

18.（12分）为了讴歌中华民族实现伟大复兴的奋斗历程，增进学生对党史的了解，某班级开展党史知识竞赛活动，现把50名学生的成绩绘制了如图所示的频率分布直方图.

（1）求a的值并估计这50名学生的平均成绩（同一组中的数据用该组区间的中点值为代表）；

（2）用分层抽样的方法从成绩在，两组学生中抽取5人进行培训，再从这5人中随机抽取2人参加校级党史知识竞赛，求这2人来自不同小组的概率.

19.（12分）已知数列的前n项和为，满足，（t为常数）.

（1）求的通项公式；

（2）若，求数列的前n项和为.

20.（12分）如图，在四棱锥中，，.

（1）在棱上是否存在点E，使得平面？说明理由；

（2）若平面平面，，，求点A到平面的距离.

21.（12分）书籍椭圆E：（）的焦点为，，且点在E上.

（1）求E的方程；

（2）已知过定点的动直线l交E于A，B两点，线段的中点为N，若为定值，试求m的值.

22.（12分）已知函数.

（1）讨论的单调性；

（2）若，关于x的方程有唯一解，求a的值.

江淮十校2022届高三第一次联考

数学（文科）试题参考答案与评分细则

一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.

1.A  解：，在复平面上对应的点的坐标为.

2.B  解：∵，∴，∵，∴，∴.

3.C  解：由已知易得.

4.C  解：当两直线平行，∴，解得或，当，两直线重合，舍去；当时，两直线平行.所以“”是“直线与直线平行”的充要条件.

5.D  解：，则，得，解得.

6.D  解：，故选D.

7.C  解：对于A，为非奇非偶函数，与函数图象不符，排除A；对于B，为非奇非偶函数，与函数图象不符，排除B；对于D，，当时，，与图象不符，排除D.故选C.

8.B  解：依题意可知，，令，，解得，.所以时，.

9.B  解：如图，在棱长等于的正方体上取四面体即为所求四面体，易得该四面体的表面积为.

10.A  解：中题意知，天干是公差为10的等差数列，地支为公差为12的等差数列，且，，因为2021年为辛丑年，则100年前的天干为“辛”，地支为“酉”，可得到1921年为辛西年.

11.A  解：

当且仅当时取等号，

∴，∴，则.

12.C  解：因为，，

因为，

①若，，此时满足；

②若，令，在恒成立，

所以在单调递增，

在恒成立，

综上可得在恒成立，，

令，，

在单调递减，单调递增，所以，所以.

二、填空题：本题共4小题，每小题5分，共20分.

13.5

解：在取得最大值5.

14.

解：因为，所以.

15.

解：由已知易得，

设点，则，

当时，取得最小值.

16.

解：不妨令点P在棱上，设，则，由勾股定理可得

，

其几何意义为x轴上一动点（）到两定点与的距离之和.其最小值即为到的距离，即.

又由平面几何知识知，当的最大值在或处取得，

当时，；当时，.

故的取值范围为.

三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.

17.解：（1）  ··································································2分

令得（）  ···································································4分

∴的单调递减区间为（）  ·······················································5分

（2）由得，

∵，∴，∴  ··································································7分

由正弦定理得，，∵，∴b的取值范围为  ···········································10分

18.解：（1）根据频率分布直方图得：，

解得  ·······································································3分

估计平均成绩为：

  ··········································································6分

（2）来自小组的有3人记为，，，来自小组的有2人记为，，从5人中随机抽取2人，基本事件为：，，，，，，，，，.

来自不同组的有，，，，，， ····················································9分

所以概率为.  ································································12分

19.解：（1）令，，可得，所以

时，，可得

所以（），又因为满足上式，所以  ················································6分

（2）解法一：因为

所以  ······································································12分

解法二：①n为偶数

②n为奇数

所以  ······································································12分

20.解：（1）存在的中点E，使得平面，  ··············································1分

证明如下：分别取，的中点E，F，连接，，，则，

又∵，∴，∵，，∴，

∴四边形为平行四边形，∴，

又∵平面，平面，∴平面.  ·······················································5分

（2）取的中点O，连接，，∴，∴，

又∵平面平面，平面平面，

平面，∴平面，  ······························································7分

设点A到平面的距离为d，则，∴.

∵平面，∴，，，∴，

易知，∴，，，

∴，，

∴，∴，

即点A到平面的距离为.  ························································12分

21.解：（1）易知，∴，而，

∴，∴椭圆E的方程为.  ·························································4分

（2）①若直线l的斜率不存在，易得，  ·············································5分

②若直线l的斜率存在，设其方程为，，，

则，联立得

，

且，，  ·····································································7分

  ··········································································8分

  ··········································································10分

要使上式为常数，必须且只需，即，

此时易知恒成立，且，符合题意.  ················································11分

综上所述，.  ································································12分

22.解：（1）由题意，可得且

①若，恒成立，则在上是增函数

②，则

所以当时，，当时，

则在上是减函数，在上是增函数

综上所述，若，在上是增函数

若，在上是减函数，在上是增函数  ················································5分

（2）中题意，可得

令，

方程有唯一解，即有唯一零点；

，

令，得.

因为，，所以（舍去），.

当时，，在是减函数；

当时，，在上是增函数.

当时，，.

若，则恒成立，不存在零点（舍）  ················································7分

若

则，即，可得

设，因为在时，是减函数，所以至多有一解.

又因为，所以，从而解得.  ·······················································9分

若，则，可得

因为，

所以在存在一个零点；

又因为

所以在存在一个零点；

因此存在两个零点（舍）. ······················································11分

综上所述，.  ································································12分