2022浙江省“七彩阳光”新高考研究联盟高三上学期8月返校考试数学试题含答案

绝密★考试结束前

2021学年第一学期浙江省“七彩阳光”新高考研究联盟返校考

考生须知：

1.本试题卷分选择题和非选择题两部分，共4页，满分150分，考试时间120分钟。

2.答题前，在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号。

3.所有答案必须写在答题卷上，写在试卷上无效。

4.考试结束后，只需上交答题卷。

选择题部分

一、选择题（本大题共10小题，每小题4分，共40分）

1.已知集合，集合，则（    ）

A.空集 B. C. D.

2.复数的虚部是（    ）

A. i B. C.1 D.-1

3.已知直线：与直线：相互垂直，则实数m的值是（    ）

A.0. B.1 C.-1 D.

4.已知，，是三个不同的平面，，.则下列命题成立的是（    ）

A.若，则  B.若，则

C.若，则 D.若，则

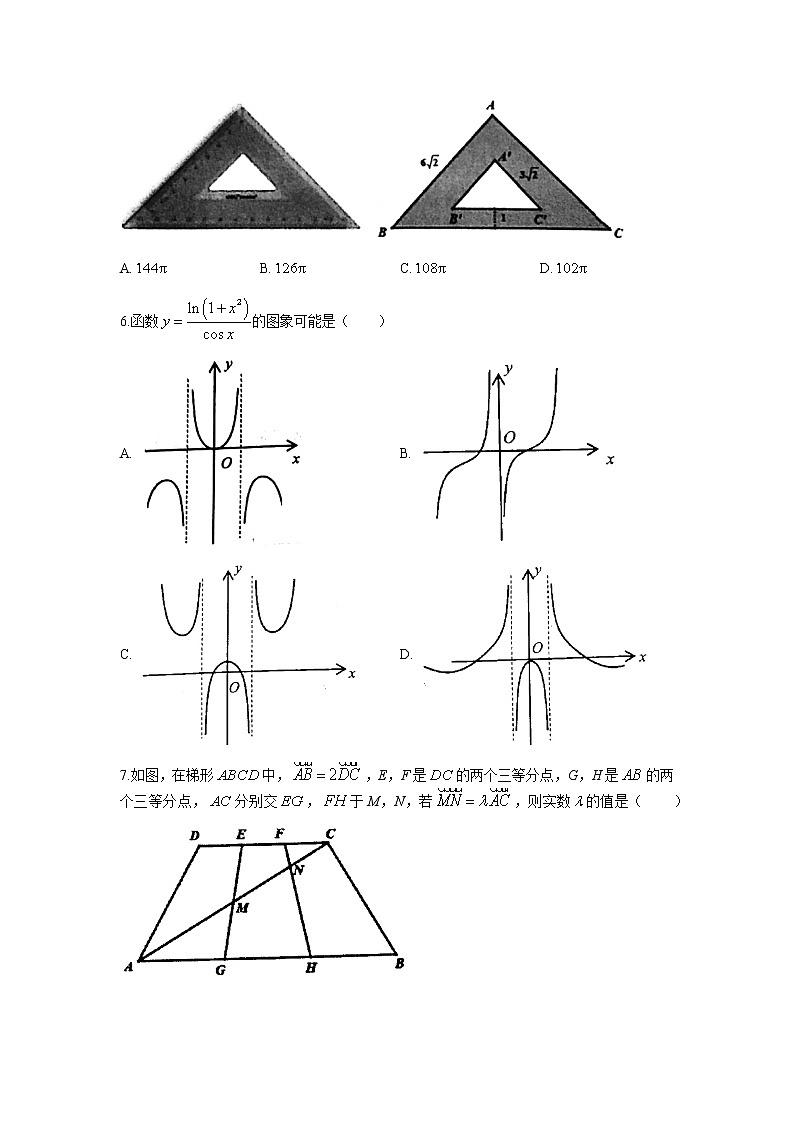
5.如图所示为学生常用的等腰直角三角形三角板，下图中，，均为等腰直角三角形，直角边长度分别为和，两斜边距离为1.现将该三角板绕斜边进行旋转，则图中阴影部分形成的几何体体积是（    ）（单位）

A. B. C. D.

6.函数的图象可能是（    ）

A.  B.

C.  D.

7.如图，在梯形中，，E，F是的两个三等分点，G，H是的两个三等分点，分别交，于M，N，若，则实数的值是（    ）

A. B. C. D.

8.已知a，，则“”是“函数存在最小值”的（    ）

A.充要条件  B.充分不必要条件

C.必要不充分条件  D.即不充分也不必要条件

9.已知双曲线C：（，）的两条渐近线为，，若双曲线C的右支上存在一点P，使得点P到，的距离之和为b，则双曲线C离心率的取值范围是（    ）

A. B. C. D.

10.设，，，（其中自然对数的底数）则（    ）

A. B. C. D.

非选择题部分

二、填空题（本大题共7小题，多空题每题6分，单空题每题4分，共36分）

11.已知角的终边经过点，则___________，___________.

12.已知，若直线l：被圆所截，则截得的弦长最短为___________.，此时直线l的方程为___________.

13.若，，则___________.

14.已知多项式，则________，___________.

15.抛掷三枚质地均匀的硬币，则事件“恰好有两枚硬币正面朝上”的概率为___________，记正面朝上的硬币枚数为随机变量，则的数学期望是___________.

16.设的三边a，b，c所对的角分别为A，B，C.若的面积为，则的最小值是___________.

17.已知平面向量，，满足，，且，则当取到最小值时，___________.

三、解答题（本大题共5小题，共74分，解答应写出文字说明、证明过程和演算步骤）

18.（本小题满分14分）已知函数.

（Ⅰ）求函数的单调递增区间；

（Ⅱ）若函数（）在上有两个零点，求m的取值范围.

19.（本小题满分15分）如图，在四棱锥中，底面为正方形，，为等边三角形.

（Ⅰ）求证：平面；

（Ⅱ）若M为棱的中点，求直线与平面所成角的正弦值.

20.（本小题满分15分）已知数列的前n项积为，，且对一切均有.

（Ⅰ）求证：数列为等差数列，并求数列的通项公式；

（Ⅱ）若数列的前n项和为，求证：.

21.（本小题满分15分）如图，已知抛物线C：（）的焦点为，D为x轴上位于F右侧的点，点A为抛物线C在第一象限上的一点，且，分别延长线段，交抛物线C于M，N.

（Ⅰ）若，求直线的斜率；

（Ⅱ）求三角形面积的最小值.

22.（本小题满分15分）

已知，，（其中e为自然对数的底数）.

（Ⅰ）求函数的单调区间；

（Ⅱ）若，函数有两个零点，，求证：.

高三数学学科答案

一、选择题（本大题共10小题，每小题4分，共40分）

试题解析：

第5题：大的三棱锥体积减去挖空部分（可以看做2个圆台体积减去1个圆柱体积）

，

.

第6题：是偶函数，排除B，当时，，，；

第7题：，，不妨设，则，

，，，选A.

第8题：，函数存在最小值（也可从图像角度看，当时，直线斜率非负），，反之，可举反例，，故选C.

第9题：两条渐近线方程为：，设，

P在双曲线C的右支上一点，故，，，，，故选C.

第10题：令，则，，，考虑到，可得，化简得等号当且仅当时取到，故时，排除A，B，下面比较a，b大小，由得，，故，故选D.

高三数学学科答案第2页共11页

二、填空题（本大题共7小题，多空题每题6分，单空题每题4分，共36分）

11.     12.     13.4   14.1  23   15.     16.   17.

试题解析

第14题：

考虑一次项系数：；下面赋值法：令，得：；令，得

，故.

第15题：

，服从二项分布），故，.

第16题：

的面积为，得

原式

，其中，当时取到最小值.（当，，时取到最小值）

第17题：

由，得：

，进一步得到：

，又，故，

当且仅当，，，

解得：，，；

或，，时取等号，

当，，时，

，

.

∴

当，，时，

，

.

∴

综上

三、解答题（本大题共5小题，共74分）

18.（7+7=14分）

（Ⅰ）（2分）

（4分）（代入给1分）

函数的单调递增区间即是

函数的单调递减区间（5分）

由，得，（6分）

所以单调增区间为，（7分）

（Ⅱ）记，函数（）在上有两个零点，即是函数，的图像与直线有两个交点（8分）

由（1）的解答知，故

（10分）

∵，∴，的图像如图所示，（12分）

数形结合，可知（14分）（结论端点开闭错误扣1分）

19.（7+8=15分）

【参考答案】：（I）证明：设，则

取中点为H，连接，，（1分）

∵为等边三角形，∴，（2分）

又，，∴面（3分）

∴，H为中点，∴（4分）

∴，∴（5分），同理由，得（6分）

又，∴平面（7分）

（Ⅱ）方法一：如图，设O为底面正方形的中心，连接，，交点记为F，

由（Ⅰ）可知平面，∴（8分）

又，∴面；∴面面，（9分）

∴在平面的射影在直线上，

为直线与平面所成角的平面角．（10分）

在中，，，，

，（12分）（线段长度有错酌情给1分）

∴（14分）

∴（15分）

方法二：底面是是正方形，由（I）可知，，两两垂直，分别以，，所在的直线为x，y，z轴建立空间直角坐标系．（8分）

设，则有，，，，（10分）

设平面的法向量为，∵，（11分）

则有：∴（13分）

又有，

设直线与平面所成角为

∴（15分）

备注：用等体积法求角，对应评分标准酌情给分。

20（8+7=15分）

【参考答案】

（Ⅰ）∵对一切均有，∴（1分）

又，（2分）

∴，即（3分）

∴时，，得：（5分）

∴为等差数列，首项，公差

∴，（7分）

∴一切，（8分）

（Ⅱ）∵，∴（9分）

∴（10分）

先证明，对一切，（11分）

令，则当时，（12分）

即在上单调递减，（13分）

故，∴，（14分）

∴

∴（15分）

备注：最后一部分也可直接求导等其他方法，对应评分标准酌情给分。

21.（8+7=15分）

【参考答案】：

解法一：（1）解：∵，∴抛物线C的方程为（1分）

设，点A为抛物线C在第一象限上的一点，故；

由得，（2分）

∴，直线：

联立得：，∴（4分）

进一步得，直线：，

联立得：，∴，∴（5分）

又∵，∴，即（6分）

代入得，化简得：，又，∴（7分）

∴  ∴．（8分）

（2）由（1）知，（10分）

（11分）

直线：即 （12分）

（13分）

（14分）

当且仅当时，S取到最小值16.（15分）

解法二：

（I）解：∵，∴抛物线C的方程为（1分）

设，，，（2分）

并设直线的方程为，

代入，得，

∴，即 ……①（3分）

∵，∴（4分）

设直线的方程为，代入，得，

∴，即……②（5分）

又∵，∴，即（6分）

把①，②代入上式得：

整理得：，解得：或（舍去），（7分）

∴  ∴．（8分）

（Ⅱ）解：抛物线C的方程为，设，，，

由（Ⅰ）的解答过程得：，，

∵A，F，M共线，∴（9分）

∵A，D，N共线，∴（10分）

分别记，的面积为，则

（11分）

另一方面，，（12分）

∴

∵，∴，∴，（14分）

当且仅当时，取到最小值16.（15分）

22.（7+8=15分）

【参考答案】:

（I）解：（2分）

∵，∴时，，

∴时，增区间为：，减区间为：；（4分）

时，，∴时，增区间为：；（5分）

时，，，

∴时，增区间为：，减区间为：；（7分）

（备注：单调区间开闭不扣分，但处应为开。）

（Ⅱ）解：由（1）知，时，增区间为：，减区间为：；

且时，，，函数的大致图像如下图所示

（9分）

因为时，函数有两个零点，，所以，即，

不妨设，则；先证：，即证：

因为，所以，又在单调递增，所以即证：

又，所以即证：，（11分）

令函数，，

则

因为，所以，，故

函数在单调递增，所以

因为，所以，，即（14分）

所以.（15分）

（Ⅱ）解法二：因为时，函数有两个零点，，

则两个零点必为正实数，（）

等价于有两个正实数解；（9分）

令（）

则（），在单调递增，在单调递减，且（10分）

令，，则

（11分）

所以在单调递增，（12分）

又，故，

又，所以，

又，所以，，

又在单调递增，所以（14分）（中间过程可酌情给1分）

所以.（15分）

（Ⅱ）解法三：还可能出现以下证明方法：

因为时，函数有两个零点，，

则两个零点必为正实数，（）

等价于有两个正实数解；（9分）

则，

因为.......，所以（给出证明得3分，否则扣这3分）（12分）

由得，（14分）

所以.（15分）

备注：若用对数均值不等式证明需对用到的对数均值不等式给与证明，否则扣3分。）