2021广东省新高考普通高中联合质量测评新高三省级摸底考试数学含解析

绝密★启用前

2021年广东省新高考普通高中联合质量测评

新高三省级摸底联考

数学试卷

本试卷共4页，22题。全卷满分150分。考试用时120分钟。

注意事项：

1.答题前，先将自己的姓名、考号等填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2.选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3.填空题和解答题的作答：用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4.考试结束后。请将本试题卷和答题卡一并上交。

一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1.设z＝1＋i，则|x3|为

A.     B.2     C.2     D.3

2.已知集合A＝{x|x2＋4x－12>0}，B＝{x|x<a}，若A∪B＝R，则a的取值范围为

A.[－6，＋∞)     B.(－6，＋∞)     C.[2，＋∞)     D.(2，＋∞)

3.已知命题p：∀a，b>0，，命题q：∀a，b∈R，，则下列命题为真命题的是

A.p∧q     B.p∨¬q     C.p∧¬q     D.p∨q

4.已知sinα＋cosα＝，α∈(0，π)，则tanα＝

A.     B.     C.－     D.－

5.四名同学各掷骰子5次，分别记录每次骰子出现的点数，根据四名同学的统计结果，可以判断出一定没有出现点数6的是

A.平均数为3，中位数为2     B.中位数为2，众数为2

C.平均数为2，方差为2.4      D.中位数为3，方差为2.8

6.若数列{an}满足＝m(n∈N*，m为常数)，则称数列{an}为等幂数列，已知数列{an}为等幂数列，且a＝2，a2＝4，Sn为数列{an}的前n项和，则S2021＝

A.6060     B.6062     C.6064     D.6066

7.过点P(－1，－2)的两条直线与抛物线C：x2＝4y分别相切于A，B两点，则三角形PAB的面积为

A.     B.3     C.27     D.

8.在平面直角坐标系中，定义P(x1，y1)，Q(x2，y2)两点之间的折线距离为d(P，Q)＝|x1－x2|＋|y1－y2|，设点P是圆x2＋y2＝1上一点，点Q是直线3x－4y－9＝0上一点，则d(P，Q)的最小值为

A.     B.1     C.     D.

二、多项选择题：本题共4小题，每小题5分，共20分。在每小题给出的选项中，有多项符合题目要求。全部选对的得5分，部分选对的得2分，有选错的得0分。

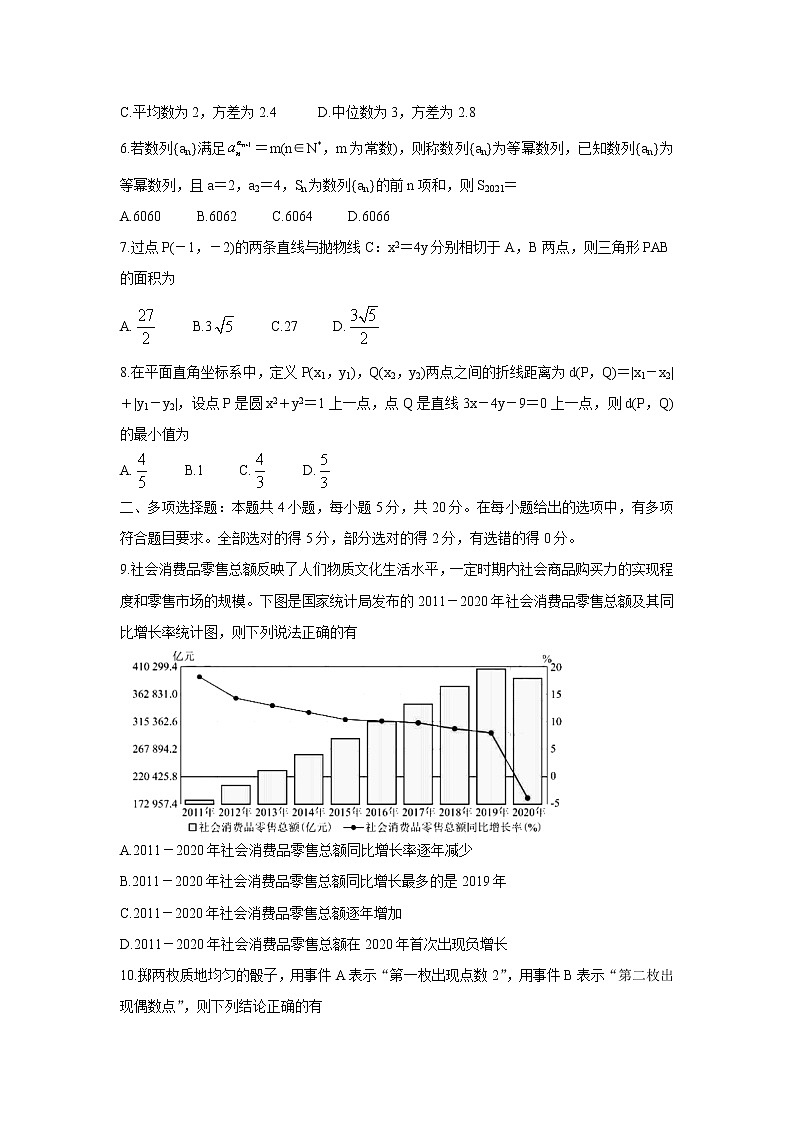
9.社会消费品零售总额反映了人们物质文化生活水平，一定时期内社会商品购买力的实现程度和零售市场的规模。下图是国家统计局发布的2011－2020年社会消费品零售总额及其同比增长率统计图，则下列说法正确的有

A.2011－2020年社会消费品零售总额同比增长率逐年减少

B.2011－2020年社会消费品零售总额同比增长最多的是2019年

C.2011－2020年社会消费品零售总额逐年增加

D.2011－2020年社会消费品零售总额在2020年首次出现负增长

10.掷两枚质地均匀的骰子，用事件A表示“第一枚出现点数2”，用事件B表示“第二枚出现偶数点”，则下列结论正确的有

A.事件A与事件B是互斥事件     B.事件A与事件B是独立事件

C.P(AB)＝                    D.P(A∪B)＝

11.如图，延长正方形ABCD的边CD至点E，使得DE＝CD，动点P从点A出发，沿正方形ABCD的边按逆时针方向运动一周后回到点A，若，则下列判断正确的是

A.满足λ＋μ＝2的点P必为BC的中点      B.满足λ＋μ＝4的点P有两个

C.满足λ＋μ＝3的点P有且只有一个        D.满足λ＋μ＝1的点P有两个

12.在棱长为1的正方体ABCD－A1B1C1D1中，已知E为线段B1C的中点，点F和点P分别满足，，其中λ，µ∈[0，1]，则下列说法正确的是

A.当λ＝时，三棱锥P－EFD的体积为定值

B.当µ＝时，四棱锥P－ABCD的外接球的表面积是

C.PE＋PF的最小值为

D.存在唯一的实数对(λ，µ)，使得EP⊥平面PDF

三、填空题：本题共4小题，每小题5分，共20分。

13.已知x＝0是函数f(x)＝xln(a－x)的极值点，则a＝         。

14.已知f(x)是奇函数，当x<0时，f(x)＝ln(ax)，若f(e)＝1，则a＝         。

15.已知非零向量a与b满足|a＋b|＝|a－b|＝|a|，则向量a－b和向量b的夹角是         。

16.已知椭圆C：的左右焦点为F1，F2，过C上一点P作直线x＝a的垂线，垂足为Q。若四边形F1PQF2为菱形，则椭圆C的离心率为         。

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

17.(本小题满分10分)

已知△ABC的内角A，B，C的对边长分别为a，b，c，D为BC上的点，AD平分∠BAC，∠BAC＝，在以下两个条件中任选一个作为条件，求tanB。

①，②△ABD的面积S△ABD是△ACD的面积S△ACD的倍。

注：如果选择两个条件分别解答，按第一个解答计分。

18.(本小题满分12分)

已知Sn是正项数列{an}的前n项和，满足a1＝1，且an＝(n∈N*，n≥2)。

(1)求数列{an}的通项公式；

(2)设bn＝，求证：数列{bn}的前n项和Tn<。

19.(本小题满分12分)

如图，四棱锥P－ABCD中，底面ABCD是直角梯形，AD//BC，∠BAD＝90°，已知PA＝PC＝3，AD＝2，AB＝，BC＝3。

(1)证明：AC⊥PD；

(2)若二面角P－AC－B的余弦值为－，求四棱锥P－ABCD的体积。

20.(本小题满分12分)

体育交流是学校之间交流的重要方式。甲乙两校定期举办击球比赛，规定：把从裁判发球哨响开始到之后裁判第一哨响止，叫做一回合。每一回合中，发球队赢球后得分1分，另一队得零分，在下一回由发球队继续发球；发球队输球后，比赛双方均得零分，下一回合由另一队发球。甲乙两队正在进行这种击球比赛，假设每一回合甲队贏球的概率是，乙队赢球的概率是，且各回合比赛的结果相互独立。

(1)第一回合由甲队发球，在连续三个回合中，求甲队得1分的概率；

(2)比赛进入决胜局，两队得分均为25分。在接下来的比赛中，甲队第一回合发球，若甲乙两队某一队得分比对方得分多2分，则比赛结束，得分多的队伍获胜。求在比赛四回合以内(包含第四回合)，甲队获胜的概率。

21.(本小题满分12分)

设双曲线C：－y2＝1，其右焦点为F，过F的直线l与双曲线C的右支交于A，B两点。

(1)求直线l倾斜角θ的取值范围；

(2)直线l交直线x＝于点P，且点A在点P，F之间，试判断是否为定值，并证明你的结论。

22.(本小题满分12分)

已知函数f(x)＝－1－alnx恰有两个零点x1，x2(x1>x2)。

(1)求实数a的取值范围；

(2)证明：3x1＋x2>6a。