2021南昌新建区一中高三高考押题卷（一）数学（文）试卷含答案

这是一份2021南昌新建区一中高三高考押题卷（一）数学（文）试卷含答案，共14页。试卷主要包含了“”是“”等内容，欢迎下载使用。
 新建一中2021年高考押题卷（一）文科数学一、选择题（本大题共12小题，每小题 5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。）1．复数z满足＝i，则复平面上表示复数z的点位于（   ）A．第一或第三象限     B．第二或第四象限     C．实轴     D．虚轴2．已知集合，则集合的真子集的个数为（   ）A． B． C． D．3．“”是“”（   ）
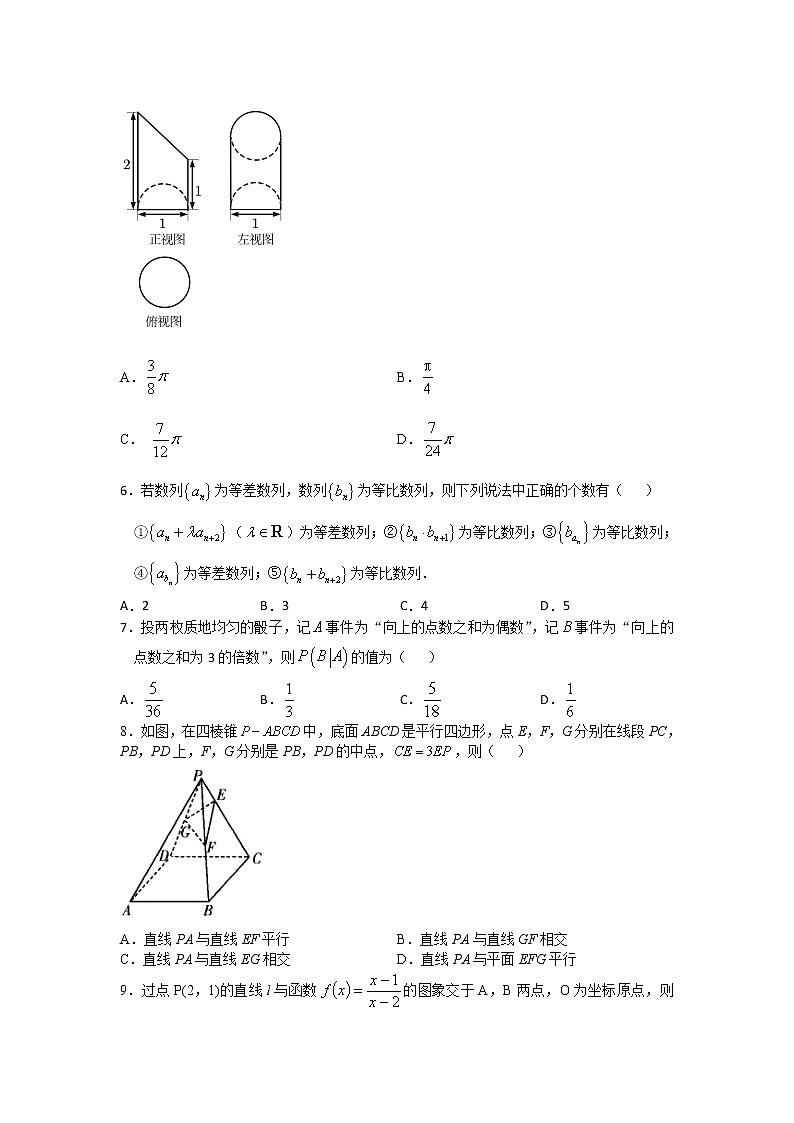
A．充分不必要条件 B．必要不充分条 C．充要条件      D．既不充分也不必要条4．2020年，我国在联合国大会上明确提出二氧化碳排放力争于2030年前达到峰值，努力争取2060年前实现碳中和。在今年全国两会上，“碳达峰”与“碳中和”被首次写入政府工作报告。这不仅彰显我国应对气候变化的大国担当，更是我国实现经济高质量发展的重要战略。中国、美国、欧盟和日本的“碳达峰”与“碳中和”的统计图如图所示，则下列结论中正确的是（   ）A．截止目前，中国、美国、欧盟和日本的碳排放均已达到了峰值B．中国、美国、欧盟和日本的碳排放峰值的中位数为44．12亿吨C．美国、欧盟和日本由“碳达峰”到“碳中和”所用时间相同D．与美国、欧盟和日本相比，中国计划由“碳达峰”到“碳中和”所用时间最短5．已知某几何体的三视图如图所示，则该几何体的体积为（   ）A． B．C．  D． 6．若数列为等差数列，数列为等比数列，则下列说法中正确的个数有（   ）①（）为等差数列；②为等比数列；③为等比数列；④为等差数列；⑤为等比数列．A．2 B．3 C．4 D．57．投两枚质地均匀的骰子，记事件为“向上的点数之和为偶数”，记事件为“向上的点数之和为3的倍数”，则的值为（   ）A． B． C． D．8．如图，在四棱锥中，底面ABCD是平行四边形，点E，F，G分别在线段PC，PB，PD上，F，G分别是PB，PD的中点，，则（   ）A．直线PA与直线EF平行 B．直线PA与直线GF相交C．直线PA与直线EG相交 D．直线PA与平面EFG平行9．过点P(2，1)的直线l与函数的图象交于A，B两点，O为坐标原点，则A．                 B．2                 C．5                   D．1010．已知等差数列的前n项和为，若，则下列结论错误的是（   ）A．               B．数列是公比为8的等比数列C．若，则数列的前2020项和为4040D．若，则数列的前2020项和为11．若定义在R上的奇函数，对任意两个不相等的实数，都有，则称函数为“H函数”，下列函数为“H函数”的是（  ）A． B． C．           D．12．为双曲线左支上一点，，，为其左右焦点，若的最小值为，则双曲线的离心率为（   ）A．      B．       C．           D．二、填空题（本大题共4小题，每小题5分，共20分）若满足约束条件，则有最    （填“大”或“小”）值为     14．已知圆的内接正三角形PQR的边PQ所在直线l经过点，且直线PQ与坐标轴不垂直，则直线l的方程为______________．15．若函数的值域为，试确定的取值范围是___________．16．已知三棱锥中，，E为PC的中点，且的面积为，则三棱锥的外接球的表面积为__________．三、解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤） 17．在①，②，③的面积为这三个条件中任选一个，补充在下面问题中，并解答问题．如图，在平面四边形ABCD中，，____________．（1）求BD的长；（2）求的最大值．18． 如图的三棱台，平面，，．（1）求证：平面平面；（2）若E，F分别为，的中点，求三棱锥的体积．19．宁夏西海固地区，在1972年被联合国粮食开发署确定为最不适宜人类生存的地区之一．为改善这一地区人民生活的贫困状态，上世纪90年代，党中央和自治区政府决定开始吊庄移民，将西海固地区的人口成批地迁移到更加适合生活的地区．为了帮助移民人口尽快脱贫，党中央作出推进东西部对口协作的战略部署，其中确定福建对口帮扶宁夏，在福建人民的帮助下，原西海固人民实现了快速脱贫，下表是对2016年以来近5年某移民村庄100位移民的年人均收入的统计：年份20162017201820192020年份代码12345人均年收入（千元）1．32．85．78．913．8现要建立关于的回归方程，有两个不同回归模型可以选择，模型一；模型二，即使画出关于的散点图，也无法确定哪个模型拟合效果更好，现用最小二乘法原理，已经求得模型一的方程为．（1）请你用最小二乘法原理，结合下面的参考数据及参考公式求出模型二的方程；（2）用计算残差平方和的方法比较哪个模型拟合效果更好，已经计算出模型一的残差平方和为．附：参考数据：，其中，．参考公式：对于一组数据，，…，，其回归直线的斜率和截距的最小二乘法估计公式分别为，．20．(本题12分) 已知（m，n为常数），在处的切线方程为．（Ⅰ）求的解析式；（Ⅱ）若，使得对上恒有成立，求实数a的取值范围；21．（12分）设椭圆的离心率为分别为椭圆E的左、右焦点，P为椭圆上异于左、右顶点的任一点，的周长为．（1）求椭圆E的方程；（2）直线交椭圆E于C，D两点，A，B分别为椭圆E的左、右顶点，直线AC和直线BD交于点M，求证：点M到y轴的距离为定值6．请考生在第22、23题中任选一题作答。注意：只能做选定的题目，如果多做，则按所做的第一题记分，解答时请写清题号。22． 在直角坐标系中，曲线的参数方程为（ 为参数），以坐标原点O为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．（1）求曲线极坐标方程并判断，的位置关系；（2）设直线分别与曲线 C1交于A，B两点，与交于点P，若，求 值．23．已知函数的最大值为4（其中m＞0）．（1）求m的值；（2）若a2+b2+c2＝m，求的最小值．                                高三文科数学押题卷一答案题号123456789101112答案BAADDCBDDBCA二、  小                   14．      15．       16．1．设，所以对应点在第二或第四象限2．集合，故个数为个3．因为，所以故“”是“”的充分不必要条件4．中国2020年达到峰值，A错；中位数为（48.54+74.16）÷2=61.35，B错；三地“碳达峰”时间不同，“碳中和”时间相同，C错；中国由“碳达峰”到“碳中和”用时30年，D对5．解析：观察三视图发现：该几何体的形状为圆柱从上方削去一部分，削去部分的体积为圆柱体积一半的一半即，下方挖去半个球，故几何体的体积为：，6．【解析】设数列的公差为，数列的公比为，对于①：，故①正确；对于②：，故②正确；对于③：，故③正确；对于④：不为定值，故④错误；对于⑤：，故⑤正确，【解析】投两枚质地均匀的骰子总的可能发生的情况有种，其中点数之和为偶数的可能  情况有18种，点数之和为3的倍数的可能情况为，，，，，，，，，，，，总共12种，所以，，，故选B．8．解析：如图，连接AC，BD交于点O，由四边形ABCD是平行四边形，得O为AC，BD的中点，因为F，G分别是PB，PD的中点，所以，连接PO，交GF于点M，可得，取线段PC的中点Q，连接OQ，则，又，所以，连接ME，则，所以，因此直线PA不与直线EF平行，与直线GF异面，与直线EG异面，与平面EFG平行，9．关于点对称，中点，10．解析：本题考查等差数列的通项公式与前n项和的公式、数列求和的方法．由等差数列的性质可知，，故A正确；设的公差为d，则有解得，故，则数列是公比为的等比数列，故B错误；若，则的前2020项，故C正确；若，则的前2020项和，故D正确．故选B．11．解析：对任意两个不相等的实数，都有，可得，即．若，则，可得，即，所以若函数为“H函数”，则函数为R上的奇函数，且为增函数．对于A选项，函数的定义域为，且为偶函数，不符合题意；对于B选项，函数为R上的非奇非偶函数，不符合题意；对于C选项，函数的定义域为R，且，故函数为奇函数，且在区间和上均为增函数．又函数在R上连续，所以函数为R上的增函数，符合题意．对于D选项，函数的定义域为R且为奇函数，但不恒大于零，所以函数不是R上的增函数，不符合题意；12．解析：设则由双曲线的定义得：，∴．记，，令，得（1）当时，，，单减；，，单增，∴，不合题意，舍去；（2）当时，恒成立，∴单增，∴∴解得：或∵不满足，应舍去∴当时，离心率．13．解析：在点处取最小值14．解析：由题意可知直线l的斜率存在且不为0，故可设直线l的方程为．圆化为标准方程得，圆心为，半径．由于是正三角形，则圆心C为的中心，则圆心C到直线l的距离为，所以，解得，所以直线l的方程为，即．15．【解析】令，则；令，解得或，即或，解得或，故的取值范围是．16．解析：如图，取AB的中点F，连接EF，PF，因为，所以，所以在中，．易知，则，所以．因为的面积为，所以，解得．连接FC，易知，所以，即为直角三角形，则，所以，则，所以，所以，所以E为三棱锥的外接球球心，其半径，所以外接球的表面积．17．答案：（1）选条件①．因为在平面四边形ABCD中，，所以．由，得，2分故．4分根据正弦定理得，所以．6分方案二：选条件②．因为在平面四边形ABCD中，，所以．设，则，由余弦定理得，3分即，得或（舍去），所以．6分方案三：选条件③．因为在平面四边形ABCD中，，所以．由题意得，解得．3分所以，所以．6分（2）设，则，由正弦定理得，8分所以，9分，11分其中．所以当时，取到最大值，且最大值为．12分18．解析：（1）证明：         （2）由（1）知，19．（1）令，则模型二可化为关于的线性回归问题，则，，         2分，则模型二的方程为；        5分（2）由模型二的回归方程可得，，，，，，8分，故模型二的拟合效果更好．12分20．解析：（Ⅰ），由条件可得及在处的切线方程为，得，所以．（4分）（Ⅱ）由（Ⅰ）知f（x）在上单调递减，∴f（x）在上的最小值为f（1）=1，6分故只需t3﹣t2﹣2at+2≤1，即对恒成立，令，8分易得m（t）在单调递减，[1，2]上单调递增，而   10分∴∴，即a的取值范围为。．．．（12分）21．答案：（1）设椭圆E的焦距为2c，则根据题意知，2分解得，故，因此椭圆E的方程为．4分（2）设，由（1）可知，将代入椭圆方程整理得，，所以                        6分因为直线AC的方程为，直线BD的方程为，   所以直线AC与BD的交点M的横坐标为，          8分将代入上式化简得，．所以．11分因此，点M的横坐标为6，即点M到y轴的距离为定值6．                        12分