2021莆田高二下学期期末质量监测数学试题含答案

这是一份2021莆田高二下学期期末质量监测数学试题含答案，共14页。试卷主要包含了3B， 已知，且，，等内容，欢迎下载使用。
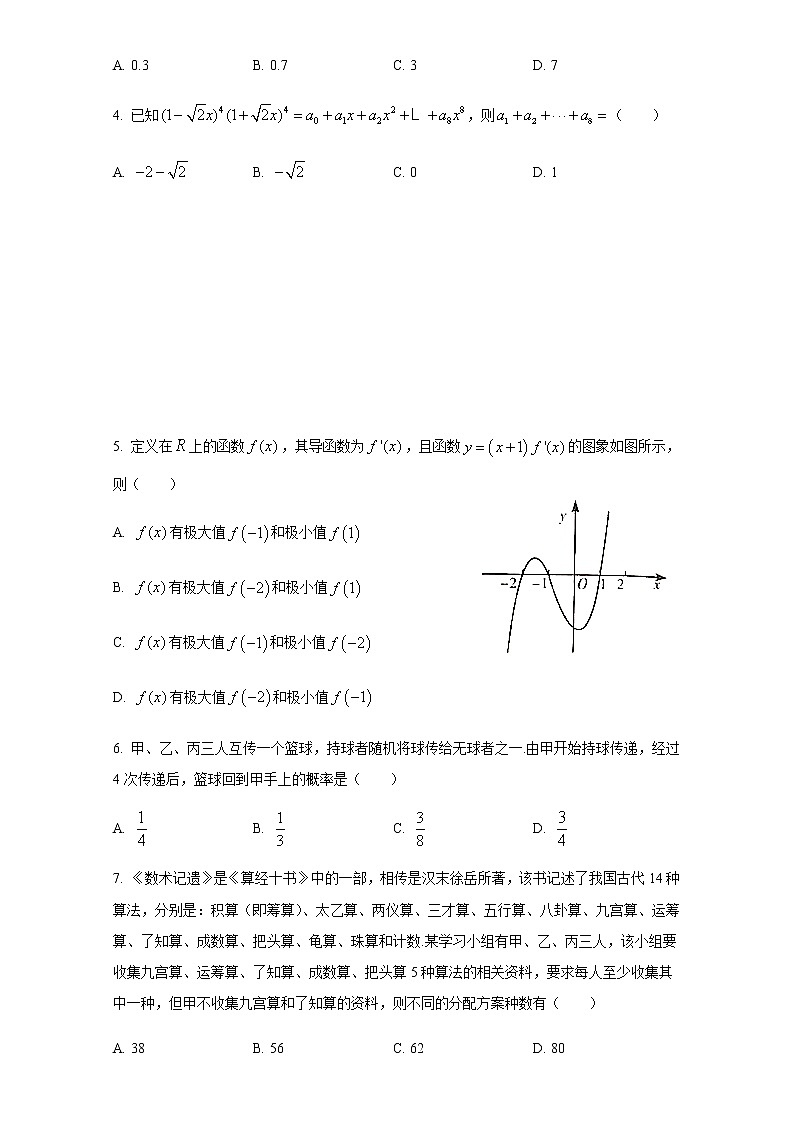
莆田市2020—2021学年下学期期末质量监测高二数学试卷满分：150分    考试时间：120分钟注意事项：1. 答题前，考生务必将自己的姓名、准考证号填写在答题卡上.2. 考生作答时，将答案答在答题卡上.请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效，在草稿纸、试题卷上答题无效.3. 选择题答案使用2B铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚.4. 保持答题卡卡面清洁，不折叠、不破损.考试结束后，将本试卷和答题卡一并交回. 一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 复数在复平面内对应点位于（    ）A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限2. 已知是函数的导函数，则（    ）A. 0 B. 2 C. 4 D. 63. 某工厂为节能降耗，经过技术改造后，生产某种产品的产量（单位：吨）与相应的生产能耗（单位：吨）的对应数据如下表：（吨）3456（吨）2.5344.5根据上表提供的数据，求得关于的线性回归方程为，则的值为（    ）A. 0.3 B. 0.7 C. 3 D. 74. 已知，则（    ）A.  B.  C. 0 D. 1     5. 定义在上的函数，其导函数为，且函数的图象如图所示，则（    ）A. 有极大值和极小值B. 有极大值和极小值C. 有极大值和极小值D. 有极大值和极小值6. 甲、乙、丙三人互传一个篮球，持球者随机将球传给无球者之一.由甲开始持球传递，经过4次传递后，篮球回到甲手上的概率是（    ）A.  B.  C.  D. 7. 《数术记遗》是《算经十书》中的一部，相传是汉末徐岳所著，该书记述了我国古代14种算法，分别是：积算（即筹算）、太乙算、两仪算、三才算、五行算、八卦算、九宫算、运筹算、了知算、成数算、把头算、龟算、珠算和计数.某学习小组有甲、乙、丙三人，该小组要收集九宫算、运筹算、了知算、成数算、把头算5种算法的相关资料，要求每人至少收集其中一种，但甲不收集九宫算和了知算的资料，则不同的分配方案种数有（    ）A. 38 B. 56 C. 62 D. 808. 已知，且，，.若，，，则（    ）A.  B.  C.  D. 二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得2分.9. 设，为两个随机事件，以下命题正确的为（    ）A. 若，是互斥事件，，，则B. 若，是对立事件，则C. 若，是独立事件，，，则D. 若，，且，则，是独立事件10. 已知某批零件的质量指标（单位：毫米）服从正态分布，且，现从该批零件中随机取3件，用表示这3件产品的质量指标值不位于区间的产品件数，则（    ）A.  B. C.   D. 11. 一袋中有大小相同的4个红球和2个白球，下列说法正确的是（    ）A. 从中任取3球，恰有一个白球的概率是B. 从中任取3球，恰有两个白球的概率是C. 从中任取3球，取得白球个数的数学期望是1D. 从中不放回地取3次球，每次任取1球，已知第一次取到红球，则后两次中恰有一次取到红球的概率为12. 已知，为函数的两个极值点，直线过，两点，则下列说法正确的是（    ）A. 是的一个极值点 B. 若的单调递减区间为，则C. 若的斜率为-2，则 D. 当时，的图象关于点对称三、填空题：本题共4小题，每小题5分，共20分.13. 复数满足：，则__________.14. 展开式中的系数为___________.（用数字作答）15. 定义在上的函数，其导函数为，若，且，则不等式的解集是___________.16. 已知甲、乙两地相距.根据交通法规，两地之间的车速应限制在.假设油价是7元/，某汽车以的速度行驶，其耗油量为，司机每小时的工资是35元.如果不考虑其他费用，那么该汽车从甲地到乙地的总费用最低是____________元，此时车速是__________.四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17. 随着智能手机的日益普飞，中学生使用手机对学校管理和学生发展带来诸多不利影响.为保护学生视力，让学生在学校专心学习，防止沉迷网络和游戏，促进学生身心健康发展，教育部于2021年1月15日下发文件《关于加强中小学生手机管理工作的通知》，对中小学生的手机使用和管理作出了相关的规定.某研究性学习小组调查研究“中学生使用智能手机对学习的影响”，对某校100名学生调查得到统计数据如下表（其中）. 不使用手机使用手机合计学习成绩优秀人数34 学习成绩不优秀人数36 合计7030100（1）求，的值，并补全表中数据；（2）运用独立性检验思想，能否判断有的把握认为中学生使用手机对学习有影响？参考公式及数据：，其中.0.150.100.050.0250.0100.0050.0012.0722.7063.8415.0246.6357.87910.828   18. 甲、乙两队进行篮球决赛，因为疫情防控需要，取消主客场，两队比赛在某“中立”场馆举行，并采取五场三胜制（当一队赢得三场胜利时，该队获胜，快赛结束）.根据以往比赛成绩，甲队每场取胜的概率为，且各场比赛结果相互独立.（1）求甲队以获胜的概率；（2）据资料统计，组织者在第一场比赛可获得门票收入200万元，以后每场比赛门票收入比上一场增加50万元，求组织者在此次比赛中获得门票总收入不少于1000万元的概率.  19. 从0，1，2，3，4，5，6中任取3个偶数和2个奇数，组成没有重复数字的五位数.（1）求其中大于50000且能被5整除的个数；（2）求其中3个偶数从左到右按由小到大排序的个数.    20. 已知函数在处取得极大值.（1）求的值；（2）若，证明：有且只有3个零点.   21. 消费扶贫是指社会各界通过消费来自贫困地区和贫困人口的产品与服务，帮助贫困人口增收脱贫的一种扶贫方式，是社会力量参与脱贫攻坚的重要途径.大力实施消费扶贫，有利于动员社会各界扩大贫困地区产品和服务消费，调动贫困人口依靠自身努力实现脱贫致富的积极性，促进贫困人口稳定脱贫和贫困地区产业持续发展.某地为了解消费扶贫对贫困户帮扶情况，随机抽取80户进行调查，并用打分来进行评估，满分为10分.下表为80户贫困户所打分数的频数统计：分数5678910频数482024168（1）求贫困户所打分数的平均值；（2）从打分不低于8分的贫困户中，用分层抽样的方法随机抽取12户.（i）分别求抽到打分为8，9，10的贫困户的户数；（ii）从以上12户中任意抽取两户，记他们所打分数之和为，求的分布列.     22. 已知函数，，曲线在点处的切线过点.（1）求的值；（2）若在处取得最小值，求的值.   莆田市2020—2021学年下学期期末质量监测高二数学试题参考解答及评分标准评分说明：1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应给分数的一半；如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数．单项选择题和单空填空题不给中间分．一、选择题：每小题5分，满分40分． 1. A 2. D 3. B 4. C 5. B 6. C 7. C 8. A二、选择题：每小题5分，满分20分．（本题为多项选择题，每小题中，全部选对得5分，部分选对得2分，有选错得0分） 9. BCD 10. AC 11. BC 12. ABD三、填空题：每小题5分，满分20分．（16题第一空2分，第二空3分） 13. 14. 15. 16.，四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．本小题主要考查独立性检验等基础知识.考查概率与统计思想. 考查数据分析和数学运算等核心素养．体现基础性和应用性. 满分10分．解：（1）由己知可得，··············································1分与联立， 得···············································2分补全表中所缺数据如下： 不使用手机使用手机合计学习成绩优秀人数学习成绩不优秀人数合计·························································4分（2）假设：使用手机与学习成绩无关，·······························5分由列联表知  ···············································6分.  ············································8分因为，所以有的把握认为中学生使用手机对学习有影响.···················10分 本小题主要考查计数原理、概率运算等基础知识. 考查运算求解能力、应用意识. 考查分类与整合思想、概率与统计思想.考查逻辑推理、数学运算等核心素养. 体现基础性、综合性与应用性.满分12分．解：（1）由已知得第场甲队获胜，前场甲队胜场负场， ····················1分甲队以获胜的概率为.·········································4分（2）（法一）因为，， 所以要使组织者获得门票总收入不少于万元，本次比赛至少打场. ·························································5分打场时，甲队获胜的概率为，乙队获胜的概率为，·································7分所以打场的概率为； ········································8分若打场，则前四场甲、乙两队各胜两场， ·························9分所以打场的概率为，·········································11分所以组织者在此次比赛中获得的门票总收入不少于万元的概率为.   ·······················································12分（法二）因为，，所以要使组织者获得门票总收入不少于万元，本次比赛至少打场. ·························································5分因为比赛采用五场三胜制，所以“比赛至少打场”的对立事件为“比赛只打场”， ··············6分甲队以获胜的概率为，·······································8分乙队以获胜的概率为，·······································10分故比赛至少打场的概率为.  ····································12分所以组织者在此次比赛中获得的门票总收入不少于万元的概率为. 19.本小题主要考查计数原理、排列与组合等基础知识. 考查运算求解能力、应用意识. 考查分类与整合思想. 考查数学运算、逻辑推理等核心素养.体现基础性与应用性.满分12分．解：（1）当首位为时，个位数只能是，从余下个偶数取个有种选法，个奇数取个有种选法，将以上3个数全排列有种排法，根据分步计数原理，一共有个；               2分当首位为时，个位数是或，①当个位数为时，从余下个偶数取个有种选法，个奇数取个有种选法，将以上3个数全排列有种排法，根据分步计数原理，一共有个；               4分②当个位数为时，从余下个偶数取一个有种选法，个奇数取个有种选法，将以上3个数全排列有种排法，根据分步计数原理，一共有个；              6分根据分类计数原理，大于且被能整除的数共有个.·························································7分（2）当所选的偶数含时，从余下的个偶数再取个有种选法，个奇数取个有种选法，因为首位不能为，所以首位只能排奇数，有种选法，在后四个位置选个排另一个奇数，有种选法，剩下位置排三个偶数有种排法，根据分步计数原理，一共有个；·································9分当所选的偶数不含时，偶数只有种选法，个奇数取个有种选法，从五个位置选个排奇数有种排法，剩下位置排三个偶数有种排法，根据分步计数原理，一共有个， ································11分根据分类计数原理，个偶数从左到右按由小到大排序共有个.····································································12分20. 本小题主要考查函数的零点、导数及其应用等基础知识. 考查推理论证、运算求解、创新意识等能力. 考查函数与方程、化归与转化、分类与整合、数形结合等数学思想. 考查逻辑推理、直观想象、数学运算等核心素养. 体现基础性与综合性．满分12分．解：（1）因为，···················································1分所以，····················································2分因为在处取得极大值，所以，····················································3分解得或，··················································4分经检验，当时，在处取得极小值，不合题意，舍去；·················5分当时，在处取得极大值，满足题意；所以. ·····················································6分（2）由（1）可得，所以，···················································7分当或时，，当时，，········································8分所以单调递增区间为和，单调递减区间为，·······················9分又因为，所以，···················································11分根据零点存在性定理，得有且只有个零点. ·······················12分21.本小题主要考查分层抽样、平均数、分布列等基础知识. 考查运算求解、数据处理、应用意识等能力. 考查概率与统计等数学思想．考查数据分析、数学运算等核心素养. 体现基础性与应用性.满分12分．解：（1）.························································2分（2）（ⅰ）由频数统计表可知，打分为的贫困户比例为，所以随机抽取户，其中打分的贫困户有户，·······················3分打分的贫困户有户，········································4分打分的贫困户有户.·········································5分（ⅱ）由题意可知的所有可能取值为.································6分， ·····················································7分，······················································8分，······················································9分，······················································10分. ·······················································11分则的分布列为1617181920························································12分22. 本小题主要考查导数及其应用等基础知识. 考查推理论证、运算求解、创新意识等能力.考查函数与方程、化归与转化、分类与整合等数学思想. 考查逻辑推理、直观想象、数学运算等核心素养. 体现综合性与创新性．满分12分．解：（1）因为，所以，··············································1分，  ·····················································2分故曲线在点处的切线斜率，····································3分又因为曲线在点处的切线过点，所以，····················································4分故，解得，················································5分所以的值为. （2）当时，，，.·······················································6分令，，则，故在区间单调递增，·········································7分因为，····················································8分所以存在唯一实数，使得，即，所以，即.··················································9分当时，，从而，当时，，从而，所以在区间单调递减，在区间单调递增，··························10分故当时，取得最小值，·······································11分所以. ·····················································12分法二：令，则，····················································6分显然在上单调递增，且，所以当时，，当时，，所以在区间单调递减，在区间单调递增，····························7分故，即，当且仅当时，等号成立.故当时，，当且仅当时，等号成立，········································8分设，则在区间单调递增，且，，······································9分所以存在唯一实数，使得，故当时，取得最小值，最小值为. ··································10分由，得，即，·················································11分所以. ·······················································12分