2021【KS5U解析】北海高二下学期期末考试数学（理）试题含解析

这是一份2021【KS5U解析】北海高二下学期期末考试数学（理）试题含解析，共14页。试卷主要包含了选择题.，填空题，解答题等内容，欢迎下载使用。
2020-2021学年广西北海市高二（下）期末数学试卷（理科）
一、选择题（共12小题，每小题5分，共60分）.
1．若复数z＝，则在复平面内所对应的点位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
2．如图，从甲地到乙地有3条路，从乙地到丁地有2条路；从甲地到丙地有2条路，从丙地到丁地有4条路．则从甲地到丁地不同的路线有（　　）

A．11条 B．12条 C．13条 D．14条
3．变量x与y的数据如表所示，其中缺少了一个数值，已知y关于x的线性回归方程为＝1.2x﹣3.8，则缺少的数值为（　　）
x
22
23
24
25
26
y
23
24
▲
26
28
A．24 B．25 C．25.5 D．26
4．＝（　　）
A．ln2 B．ln C．ln D．ln3
5．若曲线y＝ex+x的一条切线l与直线x+2y﹣2021＝0垂直，则切线l的方程为（　　）
A．2x﹣y+1＝0 B．2x+y﹣1＝0 C．2x﹣y﹣1＝0 D．2x+y+1＝0
6．在极坐标系中，O为极点，曲线ρ2cosθ＝1与射线的交点为A，则|OA|＝（　　）
A．2 B． C． D．
7．已知随机变量X的分布列为P（X＝k）＝（k＝1，2，3，4，5），则P（X≥4）＝（　　）
A． B． C． D．
8．已知随机变量ξ服从正态分布N（4，62），P（ξ≤5）＝0.89，则P（ξ≤3）＝（　　）
A．0.89 B．0.78 C．0.22 D．0.11
9．抛掷两枚质地均匀的骰子，则在点数之和为6的条件下，其中一枚点数为2的概率为（　　）
A． B． C． D．
10．我们知道，13+23＝32，13+23+33＝62，13+23+33+43＝102，13+23+33+43+53＝152，…，若13+23+33+…+n3＝1296，则n＝（　　）
A．6 B．7 C．8 D．9
11．若函数f（x）＝x2﹣（a+2）x+alnx既有极大值又有极小值，则实数a的取值范围是（　　）
A．（﹣∞，2）∪（2，+∞） B．（0，2）∪（2，+∞）
C．（2，+∞） D．{2}
12．若实数a，b，c，d满足＝1，则（a﹣c）2+（b﹣d）2的最小值为（　　）
A．2 B．2 C．4 D．8
二、填空题：本题共4小题，每小题5分，共20分。
13．若复数z＝（i为虚数单位），则复数＝　 　．
14．（3x3+）7的展开式中常数项为 　 　.（用数字作答）
15．设P，Q分别为曲线C：（θ为参数）与直线l：3x﹣4y﹣6＝0上的动点，则|PQ|的最小值为 　 　．
16．设随机变量X～B（n，），且D（X）＝，则事件“X＝2”的概率为　 　
三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。
17．在平面直角坐标系xOy中，曲线C：（α是参数）．以O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos＝0．
（1）求曲线C的普通方程以及直线l的直角坐标方程；
（2）设P（﹣1，0），直线l与曲线C交于A、两点，求|PA|•|PB|的值．
18．高中阶段有这样一句话，成也数学败也数学，意思是说数学成绩好的同学总成绩也好，数学成绩不好的同学总成绩也不好．某市教育局对本届高三学生的上学期期末考试成绩进行随机调查得到如下2×2列联表：

总成绩好
总成绩不好
总计
数学成绩好
220
m
400
数学成绩不好
100
300
400
总计
n
p
q
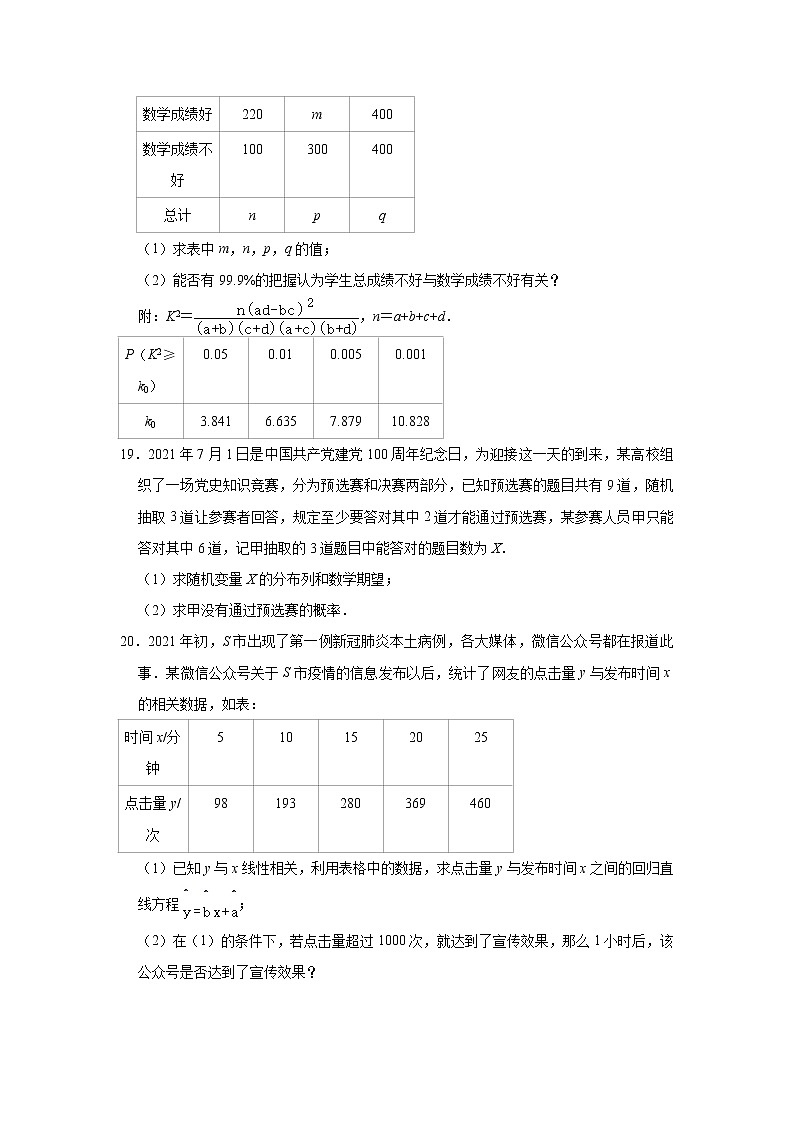
（1）求表中m，n，p，q的值；
（2）能否有99.9%的把握认为学生总成绩不好与数学成绩不好有关？
附：K2＝，n＝a+b+c+d．
P（K2≥k0）
0.05
0.01
0.005
0.001
k0
3.841
6.635
7.879
10.828
19．2021年7月1日是中国共产党建党100周年纪念日，为迎接这一天的到来，某高校组织了一场党史知识竞赛，分为预选赛和决赛两部分，已知预选赛的题目共有9道，随机抽取3道让参赛者回答，规定至少要答对其中2道才能通过预选赛，某参赛人员甲只能答对其中6道，记甲抽取的3道题目中能答对的题目数为X．
（1）求随机变量X的分布列和数学期望；
（2）求甲没有通过预选赛的概率．
20．2021年初，S市出现了第一例新冠肺炎本土病例，各大媒体，微信公众号都在报道此事．某微信公众号关于S市疫情的信息发布以后，统计了网友的点击量y与发布时间x的相关数据，如表：
时间x/分钟
5
10
15
20
25
点击量y/次
98
193
280
369
460
（1）已知y与x线性相关，利用表格中的数据，求点击量y与发布时间x之间的回归直线方程；
（2）在（1）的条件下，若点击量超过1000次，就达到了宣传效果，那么1小时后，该公众号是否达到了宣传效果？
参考公式：，．
21．在平面直角坐标系xOy中，抛物线C：y2﹣4x﹣4＝0，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为θ＝（ρ∈R）．
（Ⅰ）求抛物线C的极坐标方程；
（Ⅱ）若抛物线C与直线l交于A，B两点，求|AB|的值．
22．已知函数f（x）＝x2lnx．
（1）讨论函数f（x）的单调性；
（2）若f（x）≥ax﹣1对任意的x∈（0，+∞）成立，求实数a的取值范围．


参考答案
一、选择题（共12小题，每小题5分，共60分）.
1．若复数z＝，则在复平面内所对应的点位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
解：因为i4＝1，所以i2021＝（i4）505•i＝i，
所以z＝，则，
所以复数在复平面内所对应的点为（），
位于第一象限，
故选：A．
2．如图，从甲地到乙地有3条路，从乙地到丁地有2条路；从甲地到丙地有2条路，从丙地到丁地有4条路．则从甲地到丁地不同的路线有（　　）

A．11条 B．12条 C．13条 D．14条
解：从甲到丁分为两类，第一类：从甲过乙到丁分两步，从甲地到乙地有3条路，从乙地到丁地有2条路，
由分步乘法计数原理得，从甲到丁有6种走法；
第二类：从甲过丙到丁分两步，从甲地到丙地有2条路，从丙地到丁地有4条路，由分步乘法计数原理得，
从甲到丁有8种走法，再由分类加法计数原理得，从甲到丁共有6+8＝14种走法，
故选：D．
3．变量x与y的数据如表所示，其中缺少了一个数值，已知y关于x的线性回归方程为＝1.2x﹣3.8，则缺少的数值为（　　）
x
22
23
24
25
26
y
23
24
▲
26
28
A．24 B．25 C．25.5 D．26
解：设缺少的数为x，则，，
把代入y＝1.2x﹣3.8，得，解得x＝24．
故选：A．
4．＝（　　）
A．ln2 B．ln C．ln D．ln3
解：根据题意，＝ln（x+1）＝ln3﹣ln2＝ln，
故选：C．
5．若曲线y＝ex+x的一条切线l与直线x+2y﹣2021＝0垂直，则切线l的方程为（　　）
A．2x﹣y+1＝0 B．2x+y﹣1＝0 C．2x﹣y﹣1＝0 D．2x+y+1＝0
解：∵y＝ex+x，∴y′＝ex+1，
设切点为（x0，y0），则切线l的斜率k＝，
∴x0＝0，得，
故切线l的方程为y＝2x+1．
即2x﹣y+1＝0．
故选：A．
6．在极坐标系中，O为极点，曲线ρ2cosθ＝1与射线的交点为A，则|OA|＝（　　）
A．2 B． C． D．
解：将代入ρ2cosθ＝1得ρ2＝2，
则．
故选：B．
7．已知随机变量X的分布列为P（X＝k）＝（k＝1，2，3，4，5），则P（X≥4）＝（　　）
A． B． C． D．
解：因为随机变量X的分布列为P（X＝k）＝（k＝1，2，3，4，5），
所以，解得a＝，
所以P（X＝k）＝＝（k＝1，2，3，4，5），
则P（X≥4）＝P（X＝4）+P（X＝5）＝．
故选：B．
8．已知随机变量ξ服从正态分布N（4，62），P（ξ≤5）＝0.89，则P（ξ≤3）＝（　　）
A．0.89 B．0.78 C．0.22 D．0.11
解：∵随机变量ξ服从正态分布N（4，62），
∴这组数据对应的正态曲线的对称轴ξ＝4
∴P（ξ≤3）＝P（ξ≥5），
∵P（ξ≤5）＝0.89
∴P（ξ≥5）＝1﹣0.89＝0.11，
∴P（ξ≤3）＝0.11
故选：D．
9．抛掷两枚质地均匀的骰子，则在点数之和为6的条件下，其中一枚点数为2的概率为（　　）
A． B． C． D．
解：设“抛掷两枚骰子，两枚骰子的点数之和为6”为事件A，
“抛掷两枚骰子，其中一枚骰子的点数为2”为事件B，
则P（A）＝，P（AB）＝，
所以P（B|A）＝．
故选：B．
10．我们知道，13+23＝32，13+23+33＝62，13+23+33+43＝102，13+23+33+43+53＝152，…，若13+23+33+…+n3＝1296，则n＝（　　）
A．6 B．7 C．8 D．9
解：由于，
所以n2•（n+1）2＝5184，
所以n（n+1）＝72，所以n＝8或﹣9（负值舍去）．
故选：C．
11．若函数f（x）＝x2﹣（a+2）x+alnx既有极大值又有极小值，则实数a的取值范围是（　　）
A．（﹣∞，2）∪（2，+∞） B．（0，2）∪（2，+∞）
C．（2，+∞） D．{2}
解：因为f（x）＝x2﹣（a+2）x+alnx既有极大值又有极小值，
且，
所以f′（x）＝0有两个不相等的正实数解，
所以，且，解得a＞0，且a≠2．
故选：B．
12．若实数a，b，c，d满足＝1，则（a﹣c）2+（b﹣d）2的最小值为（　　）
A．2 B．2 C．4 D．8
解：由＝1，可得b＝ea+1，d＝c﹣2，
故（a﹣c）2+（b﹣d）2的几何意义为曲线y＝ex+1上一点（a，b）与直线y＝x﹣2上一点（c，d）间距离的平方，
对于函数y＝ex+1，令y′＝ex+1＝1，解得x＝﹣1，
即y＝ex+1在点（﹣1，1）处的切线方程为x﹣y+2＝0，切线方程与直线y＝x﹣2平行，
则函数y＝ex+1在（﹣1，1）处的切线与直线y＝x﹣2之间的距离d＝，
故（a﹣c）2+（b﹣d）2的最小值为d2＝8．
故选：D．
二、填空题：本题共4小题，每小题5分，共20分。
13．若复数z＝（i为虚数单位），则复数＝　1﹣i　．
解：∵z＝＝，
∴．
故答案为：1﹣i．
14．（3x3+）7的展开式中常数项为 　21　.（用数字作答）
解：的展开式的通项公式为＝，
令，得r＝6，所以的展开式中常数项为．
故答案为：21．
15．设P，Q分别为曲线C：（θ为参数）与直线l：3x﹣4y﹣6＝0上的动点，则|PQ|的最小值为 　1　．
解：曲线C：（θ为参数）转换为直角坐标方程为（x﹣1）2+（y﹣3）2＝4，
所以圆心（1，3）到直线3x﹣4y﹣6＝0的距离d＝，
所以|PQ|min＝3﹣2＝1．
故答案为：1．
16．设随机变量X～B（n，），且D（X）＝，则事件“X＝2”的概率为　　
解：∵随机变量X～B（n，），且D（X）＝，
∴＝，
解得n＝4，
∴事件“X＝2”的概率为：
P（X＝2）＝＝．
故答案为：．
三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。
17．在平面直角坐标系xOy中，曲线C：（α是参数）．以O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos＝0．
（1）求曲线C的普通方程以及直线l的直角坐标方程；
（2）设P（﹣1，0），直线l与曲线C交于A、两点，求|PA|•|PB|的值．
解：（1）曲线C：（α是参数），转换为直角坐标方程为，
直线l的极坐标方程为ρcos＝0，根据，转换为直角坐标方程为x﹣y+1＝0．
（2）设P（﹣1，0），直线的参数方程（t为参数），
把直线的参数方程，代入得到：；
所以|PA||PB|＝．
18．高中阶段有这样一句话，成也数学败也数学，意思是说数学成绩好的同学总成绩也好，数学成绩不好的同学总成绩也不好．某市教育局对本届高三学生的上学期期末考试成绩进行随机调查得到如下2×2列联表：

总成绩好
总成绩不好
总计
数学成绩好
220
m
400
数学成绩不好
100
300
400
总计
n
p
q
（1）求表中m，n，p，q的值；
（2）能否有99.9%的把握认为学生总成绩不好与数学成绩不好有关？
附：K2＝，n＝a+b+c+d．
P（K2≥k0）
0.05
0.01
0.005
0.001
k0
3.841
6.635
7.879
10.828
解：（1）m＝400﹣220＝180，n＝220+100＝320，p＝m+300＝480，q＝400+400＝800．
（2）因为，
因此有99.9%的把握认为学生总成绩不好与数学成绩不好有关．
19．2021年7月1日是中国共产党建党100周年纪念日，为迎接这一天的到来，某高校组织了一场党史知识竞赛，分为预选赛和决赛两部分，已知预选赛的题目共有9道，随机抽取3道让参赛者回答，规定至少要答对其中2道才能通过预选赛，某参赛人员甲只能答对其中6道，记甲抽取的3道题目中能答对的题目数为X．
（1）求随机变量X的分布列和数学期望；
（2）求甲没有通过预选赛的概率．
解：（1）由题意可知，随机变量X的可能取值为0，1，2，3，且X服从超几何分布，
所以P（X＝0）＝＝，
P（X＝1）＝＝，
P（X＝2）＝＝，
P（X＝3）＝＝，
所以随机变量X的分布列为：
X
0
1
2
3
P




所以E（X）＝0×+1×+2×+3×＝2．
（2）若甲没有通过预选赛，则甲答对了1道或0道，
所以甲没有通过预选赛的概率P＝P（X＝0）+P（X＝1）＝＝．
20．2021年初，S市出现了第一例新冠肺炎本土病例，各大媒体，微信公众号都在报道此事．某微信公众号关于S市疫情的信息发布以后，统计了网友的点击量y与发布时间x的相关数据，如表：
时间x/分钟
5
10
15
20
25
点击量y/次
98
193
280
369
460
（1）已知y与x线性相关，利用表格中的数据，求点击量y与发布时间x之间的回归直线方程；
（2）在（1）的条件下，若点击量超过1000次，就达到了宣传效果，那么1小时后，该公众号是否达到了宣传效果？
参考公式：，．
解：（1）由题意可知，，
，
，，
所以，
所以，
所以点击量y与发布时间x之间的回归直线方程为；
（2）令x＝60，可得，
所以1小时后，该公众号信息的点击量约为1000次，达到了宣传效果．
21．在平面直角坐标系xOy中，抛物线C：y2﹣4x﹣4＝0，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为θ＝（ρ∈R）．
（Ⅰ）求抛物线C的极坐标方程；
（Ⅱ）若抛物线C与直线l交于A，B两点，求|AB|的值．
解：（Ⅰ）因为x＝ρcosθ，y＝ρsinθ，
代入y2﹣4x﹣4＝0得ρ2sin2θ﹣4ρcosθ﹣4＝0，
所以抛物线C的极坐标方程为ρ2sin2θ﹣4ρcosθ﹣4＝0．
（Ⅱ）将代入抛物线C的方程得，
所以，，
，
所以，
故．
22．已知函数f（x）＝x2lnx．
（1）讨论函数f（x）的单调性；
（2）若f（x）≥ax﹣1对任意的x∈（0，+∞）成立，求实数a的取值范围．
解：（1）因为f（x）＝x2lnx，
所以f′（x）＝2x（lnx+），
令f′（x）＝0，则2x（lnx+）＝0，
所以x＝0（舍去）或x＝，
当x∈（0，）时，f′（x）＜0，
当x∈（，+∞）时，f′（x）＞0，
所以函数f（x）在区间（0，）上单调递减，在（，+∞）上单调递增．
（2）根据题意可知a≤对任意的x∈（0，+∞）成立，
令g（x）＝，
则g′（x）＝，
令h（x）＝x2lnx+x2﹣1，
h′（x）＝2xlnx+x2•+2x＝2xlnx+3x＝x（2lnx+3），
所以在（e，+∞）上，h′（x）＞0，h（x）单调递增，
在（0，e）上，h′（x）＜0，h（x）单调递减，
当x→0时，h（x）→﹣1；且h（1）＝0，
所以当x≥1时，g′（x）≥0，
当0＜x＜1时，g′（x）＜0，
所以函数g（x）在区间（1，+∞）上单调递增，在区间（0，1）上单调递减，
所以g（x）min＝g（1）＝1，
所以a≤1，
所以实数a的取值范围为（﹣∞，1]．