
2022年河北省承德市平泉市中考二模数学试题(word版无答案)
展开2022年平泉市初中毕业生模拟考试
数学试卷
本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题.
卷Ⅰ(选择题,共42分)
一、选择题(本大题共16个小题,1~10小题,每小题3分;11~16小题,每小题2分,共42分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,在菱形ABCD中,下列式子可以求出在菱形ABCD面积的是( )
A. B. C. D.
2.下列各式中正确的是( )
A. B. C. D.
3.对于,第一个因数增加1后积的变化是( )
A.增加1 B.减少3 C.增加3 D.减少4
4.若,则表示的多项式是( )
A. B. C. D.
5.如图,在围棋棋盘上有3枚棋子,如果黑棋❶的位置用有序数对表示,黑棋❷的位置用有序数对表示,则白棋③的位置可用有序数对表示为( )
A. B. C. D.
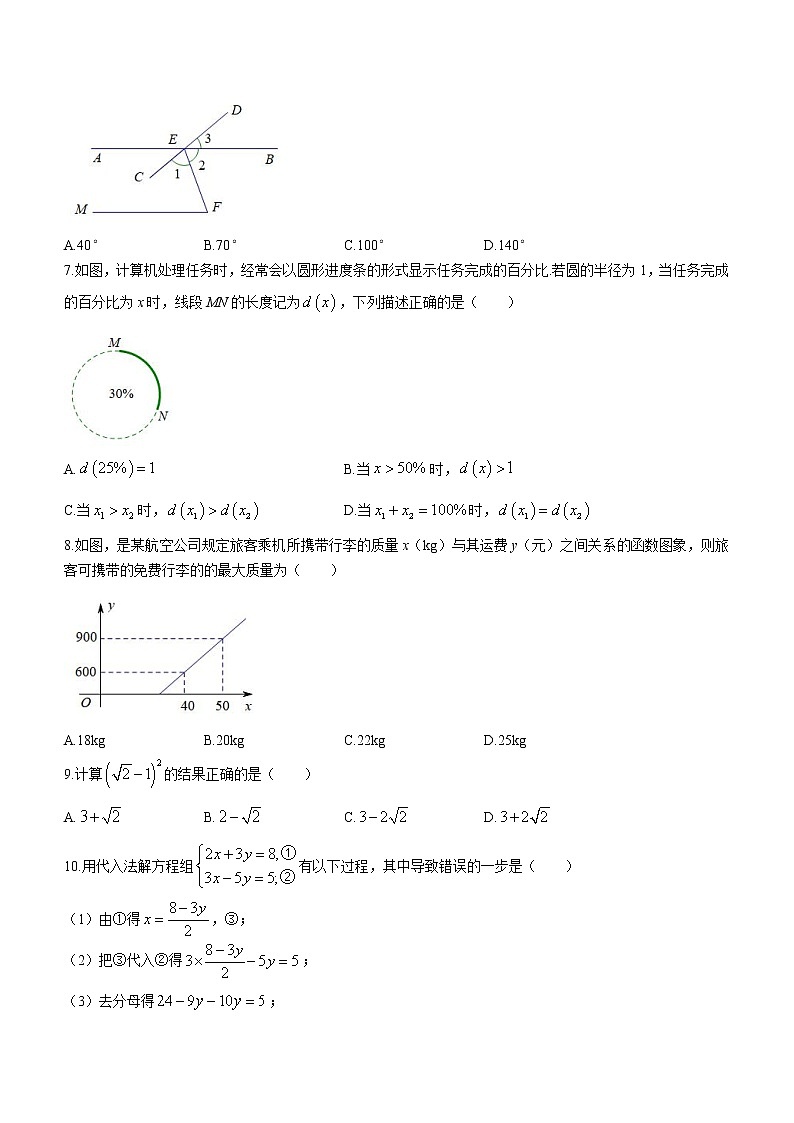
6.如图,直线AB与CD相交于点E,EF平分,.若,则( )
A.40° B.70° C.100° D.140°
7.如图,计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.若圆的半径为1,当任务完成的百分比为x时,线段MN的长度记为,下列描述正确的是( )
A. B.当时,
C.当时, D.当时,
8.如图,是某航空公司规定旅客乘机所携带行李的质量x(kg)与其运费y(元)之间关系的函数图象,则旅客可携带的免费行李的的最大质量为( )
A.18kg B.20kg C.22kg D.25kg
9.计算的结果正确的是( )
A. B. C. D.
10.用代入法解方程组有以下过程,其中导致错误的一步是( )
(1)由①得,③;
(2)把③代入②得;
(3)去分母得;
(4)解之得,再由③得.
A.(1) B.(2) C.(3) D.(4)
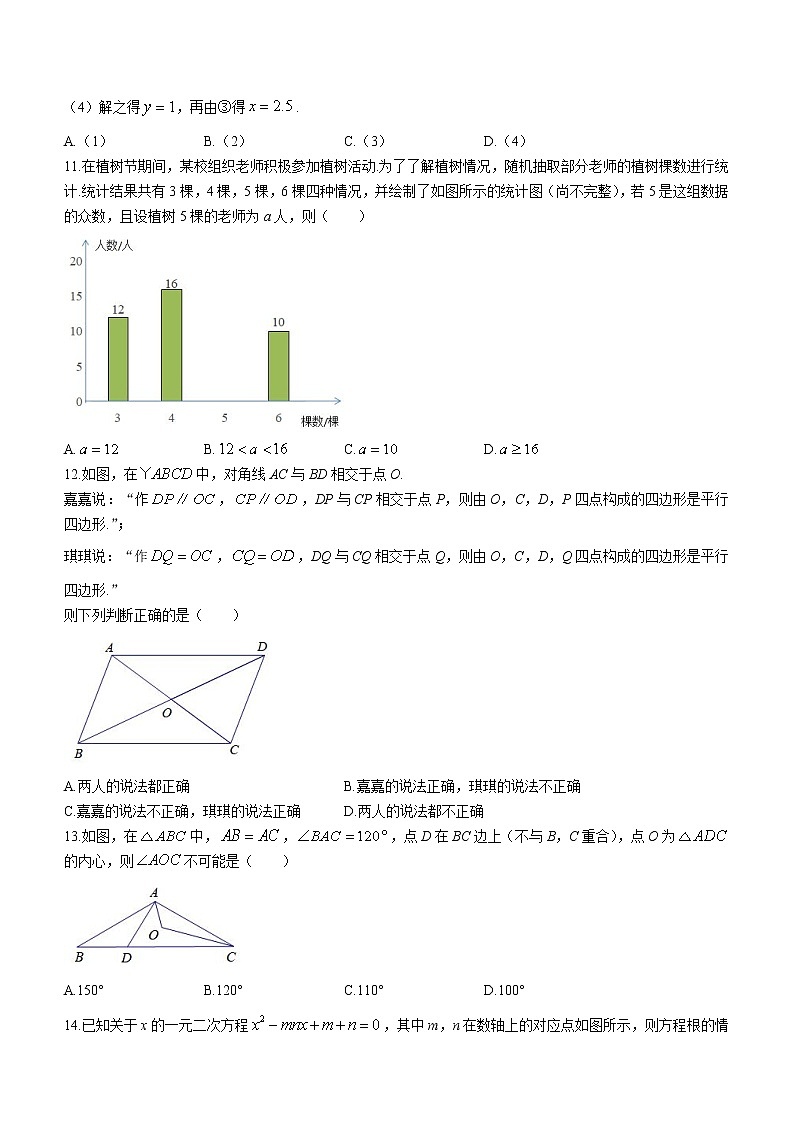
11.在植树节期间,某校组织老师积极参加植树活动.为了了解植树情况,随机抽取部分老师的植树棵数进行统计.统计结果共有3棵,4棵,5棵,6棵四种情况,并绘制了如图所示的统计图(尚不完整),若5是这组数据的众数,且设植树5棵的老师为a人,则( )
A. B. C. D.
12.如图,在中,对角线AC与BD相交于点O.
嘉嘉说:“作,,DP与CP相交于点P,则由O,C,D,P四点构成的四边形是平行四边形.”;
琪琪说:“作,,DQ与CQ相交于点Q,则由O,C,D,Q四点构成的四边形是平行四边形.”
则下列判断正确的是( )
A.两人的说法都正确 B.嘉嘉的说法正确,琪琪的说法不正确
C.嘉嘉的说法不正确,琪琪的说法正确 D.两人的说法都不正确
13.如图,在中,,,点D在BC边上(不与B,C重合),点O为的内心,则不可能是( )
A.150° B.120° C.110° D.100°
14.已知关于x的一元二次方程,其中m,n在数轴上的对应点如图所示,则方程根的情况是( )
A.有两个不相等的实数根 B.有两个相等实数根
C.没有实数根 D.无法确定
15.如图,点A,B是半径为1的圆上的任意两点,则下列说法正确的是( )
A.A,B两点间的距离可以是
B.以AB为边向内构造等边三角形,则三角形的最大面积为
C.以AB为边向内构造正方形,则正方形的面积可以为3
D.以AB为边向内构造正六边形,则正六边形的最大面积为
16.甲、乙、丙三人共同探究代数式的情况,三人的说法如下:
甲:只有当时,代数式的值为2;
乙:当x取大于2的实数时,代数式的值随x的增大而减小;
丙:无论x取何值时,代数式的值都不可能大于4.
下列判断正确的是( )
A.甲对,乙对 B.甲对,丙对 C.甲错,丙对 D.乙错,丙错
卷Ⅱ(非选择题,共78分)
二、填空题(本大题有3个小题,每小题有2个空,每空2分,共12分.把答案写在题中横线上)
17.已知:.
(1)对上式进行化简,得______;
(2)若,则______.
18.如图,在矩形ABCD中,,,点P是对角线AC上任意一点,过点P作,PQ交BC于点Q.
(1)______;
(2)连接DQ,把沿DQ折叠,当点C与点P重合时,______.
19.如图,点A在双曲线上,点B在双曲线上,轴,且交y轴于点C.
(1)连接OA,则的面积为_________;
(2)若,则k的值为______.
三、解答题(本大题共7个小题,共66分.解答应写出文字说明、证明过程或演算
步骤)
20.(本小题满分8分)
在城区老旧小区改造中,为了提高居民的宜居环境,某小区规划修建一个广场(平面图如图中阴影部分所示).
(1)用含m,n的式子表示广场(阴影部分)的面积S;
(2)若米,米,修建每平方米需费用200元,用科学记数法表示修建广场的总费用W的值.
21.(本小题满分9分)
“疫情”得到有效控制后,为加快复工复产,某企业需运输一批物资.据调查得知,1辆大货车与2辆小货车一次可以运输350箱;2辆大货车与3辆小货车一次可以运输600箱.
(1)求1辆大货车和1辆小货车一次可以分别运输多少箱物资?
(2)该企业计划用两种货车共12辆运输这批物资,若一次运输物资不少于1500箱,则至少需要大货车多少辆?
22.(本小题满分9分)
文具店有三种品牌的笔记本,价格分别是4,5,7(单位:元),从中随机拿出一个本,已知P(一次拿到5元本).
(1)求这6个本价格的众数;
(2)若琪琪已拿走一个5元本,嘉嘉准备从剩余5个本中随机拿一个本.
①所剩的5个本价格的中位数与原来6个本价格的中位数是否相同?并简要说明理由;
②嘉嘉先随机拿出一个本后不放回,之后又随机从剩余的本中拿一个本,用列表法求嘉嘉两次都拿到5元本的概率.
23.(本小题满分9分)
如图,,点E在BC上,且,.
(1)求证:;
(2)判断AC和BD的位置关系,并说明理由.
24.(本小题满分10分)
已知A,B两点之间有一条公路.甲车从A地出发匀速开往B地,甲车出发两小时后,乙车从B地出发匀速开往A地,甲车出发6小时,两车同时到达各自的目的地.两车行驶的路程之和y(千米)与甲车行驶的时间x(小时)之间的函数关系如图所示.
(1)甲车的速度为______千米/小时,a的值为______;
(2)求乙车出发后,y与x之间的函数关系式;
(3)当甲、乙两车相距180千米时,求甲车行驶的时间.
25.(本小题满分10分)
在扇形AOB中,半径,点P在OA上,连接PB,将沿PB折叠得到.
(1)如图,若,且与弧AB所在的圆相切于点B.
①求的度数;
②求OP的长.
(2)如图,与弧AB相交于点D,若点D为弧AB的中点,且,直接写出弧AB的长.
26.(本小题满分12分)
如图,抛物线L:与x轴交于点,两点,与y轴交于点C,直线l经过点B和点C,点P的坐标为.
(1)求抛物线L和直线l的解析式;
(2)当点P在L上时,求m的值;
(3)过点P作y轴的平行线,分别与直线l、抛物线L交于点M、N.
①当线段,求m的值;
②若P,M,N三点不重合,当其中两点关于第三点对称时,直接写出m的值.
河北省承德市平泉市2023-2024学年七年级下学期期末数学试题(无答案): 这是一份河北省承德市平泉市2023-2024学年七年级下学期期末数学试题(无答案),共7页。
河北省承德市平泉市2021-2022学年七年级下学期期末数学试题(word版含答案): 这是一份河北省承德市平泉市2021-2022学年七年级下学期期末数学试题(word版含答案),共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
河北省承德市平泉市2021-2022学年九年级上学期期末数学试题(word版含答案): 这是一份河北省承德市平泉市2021-2022学年九年级上学期期末数学试题(word版含答案),共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












